北师大版数学五年级上册第六单元组合图形的面积 测试卷(含答案)
文档属性
| 名称 | 北师大版数学五年级上册第六单元组合图形的面积 测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 263.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
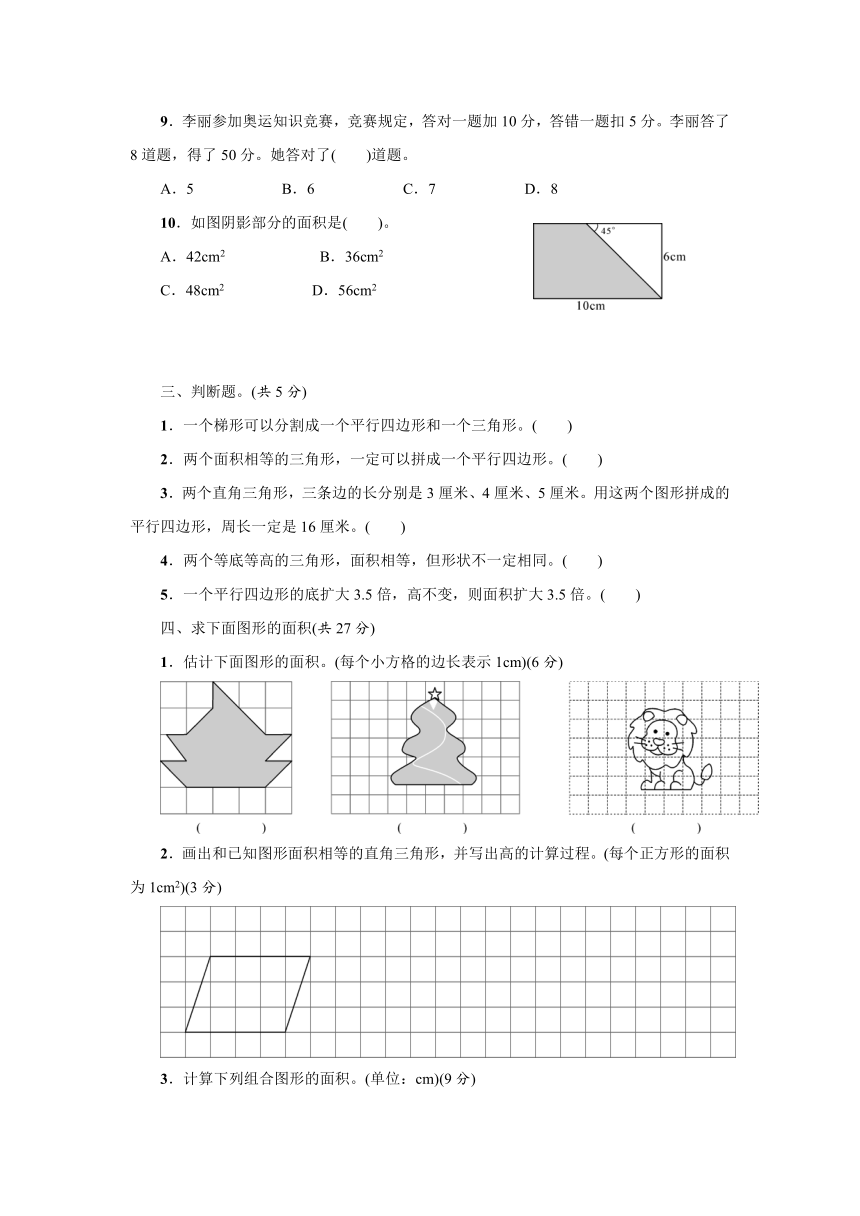
| 更新时间 | 2022-01-13 10:52:10 | ||
图片预览


文档简介
第六单元测试卷
时间:60分钟 满分:100分
题号 一 二 三 四 五 总分
得分
一、填空题。(每空1分,共24分)
1.一个梯形上底与下底的和是1.5分米,高是6.6厘米,面积是( )。
2.平行四边形的底是3dm5cm,高是底的1.2倍,它的面积是( )。
3.两个( )的梯形可以拼成一个平行四边形。
4.在( )里填上合适的数。
6.4km2=( )公顷 6170cm2=( )dm2 70cm2=( )m2
750000m2=( )平方千米 8000平方米=( )公顷
5.在○里填上“>”“<”或“=”。
800平方厘米8平方分米 1.9平方米19平方分米
60公顷60000平方米 1.2平方千米120000平方米
6.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则一条腰长是( )厘米。
7.一个平行四边形,面积是12m2,若底和高都扩大2倍,它的面积是( )m2。
8.一个三角形和一个平行四边形的面积与底相等,平行四边形的高是1.8分米,三角形的高是( )分米。
9.一个梯形的面积是44平方分米,上、下底之和为11分米,它的高是( )分米。
10.一个梯形,它的下底是8厘米,如果将它的上底增加3厘米,正好变成一个平行四边形,这时面积增加15平方厘米,原来的梯形面积是( )平方厘米。
11.如右图,按照这样的规律排列下去,第六个点阵中点的个数是( )。
12.用小棒按照如下的方式摆图形。
摆1个八边形需要8根小棒,摆2个八边形需要15根小棒,……,摆50个八边形需要( )根小棒;如果摆这样的八边形用了267根小棒,你知道摆了( )个八边形。
13.如图阴影部分是( )形,它的底等于小正方形的( ),高等于大正方形的( ),小正方形边长4cm,大正方形边长6cm,阴影部分面积是( )cm2。
二、选择题。(共20分)
1.能拼成一个平行四边形的两个三角形必须具备( )。
A.面积相等 B.形状相同 C.完全一样 D.任意两个均可
2.如图中,三角形AOD和三角形BOC的面积相比,( )大。
A.三角形AOD B.一样
C.三角形BOC D.无法比较
3.如果两个三角形的面积相等,则这两个三角形( )。
A.形状完全相同 B.底和高相等 C.底和高的乘积相等
4.甲、乙两个三角形面积相等,甲的底边是乙的2倍,甲底边上的高是乙对应底边上高的( )。
A.2倍 B. C.相等 D.无法确定
5.梯形的面积是48平方厘米,高是8厘米,则上、下底的和是( )厘米。
A.12 B.6 C.24
6.面积为15公顷的长方形鱼塘,宽是300米,长是( )米
A.50 B.500 C.5
7.一个教室的长为8米,宽为6米,大约( )个这样的教室面积约1公顷。
A.10 B.200 C.2000
8.阴影部分的面积与其他阴影部分的面积不相等的是( )。
9.李丽参加奥运知识竞赛,竞赛规定,答对一题加10分,答错一题扣5分。李丽答了8道题,得了50分。她答对了( )道题。
A.5 B.6 C.7 D.8
10.如图阴影部分的面积是( )。
A.42cm2 B.36cm2
C.48cm2 D.56cm2
三、判断题。(共5分)
1.一个梯形可以分割成一个平行四边形和一个三角形。( )
2.两个面积相等的三角形,一定可以拼成一个平行四边形。( )
3.两个直角三角形,三条边的长分别是3厘米、4厘米、5厘米。用这两个图形拼成的平行四边形,周长一定是16厘米。( )
4.两个等底等高的三角形,面积相等,但形状不一定相同。( )
5.一个平行四边形的底扩大3.5倍,高不变,则面积扩大3.5倍。( )
四、求下面图形的面积(共27分)
1.估计下面图形的面积。(每个小方格的边长表示1cm)(6分)
2.画出和已知图形面积相等的直角三角形,并写出高的计算过程。(每个正方形的面积为1cm2)(3分)
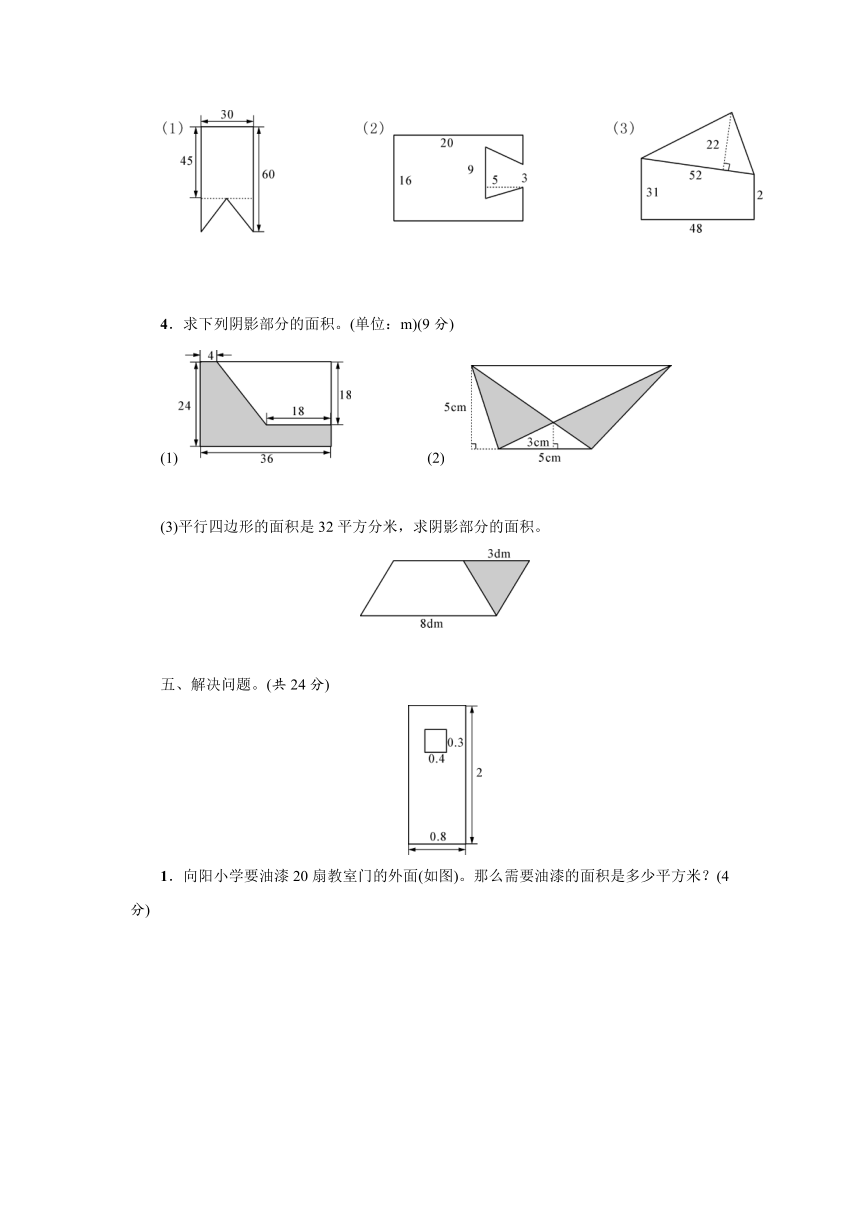
3.计算下列组合图形的面积。(单位:cm)(9分)
4.求下列阴影部分的面积。(单位:m)(9分)
(1) (2)
(3)平行四边形的面积是32平方分米,求阴影部分的面积。
五、解决问题。(共24分)
1.向阳小学要油漆20扇教室门的外面(如图)。那么需要油漆的面积是多少平方米?(4分)
2.有一个长25米、宽20米的花坛,如果在这个花坛的四周修3米宽的小路(如图),小路的面积是多少平方米?(4分)
3.一块长方形草地,长是15米,宽是10米,中间铺一条石子路(如图)。草地部分面积有多大?(4分)
4.小明家一面外墙墙皮脱落,要重新粉刷,每平方米需要用0.6千克涂料。如果涂料的价格是每千克12元,粉刷这面墙需要多少元?(4分)
5.在一个停车场上,停了汽车和摩托车一共32辆。其中汽车有4个轮子,摩托车有2个轮子,这些车一共有88个轮子。求汽车和摩托车各有多少辆?(4分)
6.一个三角形的底长5m,如果底延长1m,高不变,那么面积就增加1.5m2(如图),原来三角形的面积是多少平方米?(4分)
参考答案
第六单元测试卷
一、1.49.5厘米2 2.1470cm2 3.完全相同
4.640 61.7 0.007 0.75 0.8 5.= > > > 6.12
7.48 8.3.6 9.8 10.65
11.21 12.351 38 13.三角 边长 边长 12
二、1.C 2.B 3.C 4.B 5.A
6.B 7.B 8.D 9.B 10.A
三、1.√
2.× 解析:两个完全相同的三角形,一定可以拼成一个平行四边形。
3.× 解析:周长可以是14cm。
4.√
5.√
四、1.略 2.略
3.(1)30×60-[(30×15)÷2]=1800-225=1575(cm2)
(2)20×16-[(3+9)×5÷2]=320-30=290(cm2)
(3)52×22÷2+[(2+31)×48÷2]=572+792=1364(cm2)
4.(1)24×36-[(18+32)×18÷2]=864-450=414(m2)
(2)(5×5÷2-5×3÷2)×2=10(m2)
(3)高:32÷8=4(dm) 3×4÷2=6(dm2)
五、1.0.8×2=1.6(m2) 0.3×0.4=0.12(m2) (1.6-0.12)×20=29.6(m2) 解析:要求油漆20扇教室的门的外面需要油漆的面积,要先求出一扇门的外面需要油漆的面积,我们可以运用分割法将图中的一扇门,分割成两部分,一部分是长为2米,宽为0.8米的一个大长方形;另一部分是门上的小窗,长为0.4米,宽为0.3米的小长方形,用大长方形的面积减去小长方形的面积即可得到油漆一扇门的外面需要油漆的面积。再用油漆一扇门的面积乘20扇门便可得到一共需要油漆的面积。
2.(25+3×2)×(20+3×2)=806(m2) 25×20=500(m2) 806-500=306(m2) 解析:用外面大长方形的面积减去里面小长方形的面积就等于小路的面积。
3.15×10=150(m2) 1×15=15(m2) 150-15=135(m2) 解析:用大长方形的面积减去里面平行四边形面积=草地部分面积
4.8×3.5+8×2÷2=28+8=36(m2) 36×0.6×12=259.2(元) 解析:先求整面墙的面积=三角形面积+长方形的面积,总价=涂料的数量×单价。
5.假设全部都是汽车,那么轮子就有32×4=128(个) 摩托车:(128-88)÷(4-2)=20(辆) 汽车:32-20=12(辆)
6.高:1.5×2÷1=3(m) 5×3÷2=7.5(m2) 解析:要求原来三角形的面积,先求三角形的高,根据阴影部分面积和底求高:1.5×2÷1=3(m),再求原来三角形的面积:5×3÷2=7.5(m2)。
时间:60分钟 满分:100分
题号 一 二 三 四 五 总分
得分
一、填空题。(每空1分,共24分)
1.一个梯形上底与下底的和是1.5分米,高是6.6厘米,面积是( )。
2.平行四边形的底是3dm5cm,高是底的1.2倍,它的面积是( )。
3.两个( )的梯形可以拼成一个平行四边形。
4.在( )里填上合适的数。
6.4km2=( )公顷 6170cm2=( )dm2 70cm2=( )m2
750000m2=( )平方千米 8000平方米=( )公顷
5.在○里填上“>”“<”或“=”。
800平方厘米8平方分米 1.9平方米19平方分米
60公顷60000平方米 1.2平方千米120000平方米
6.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则一条腰长是( )厘米。
7.一个平行四边形,面积是12m2,若底和高都扩大2倍,它的面积是( )m2。
8.一个三角形和一个平行四边形的面积与底相等,平行四边形的高是1.8分米,三角形的高是( )分米。
9.一个梯形的面积是44平方分米,上、下底之和为11分米,它的高是( )分米。
10.一个梯形,它的下底是8厘米,如果将它的上底增加3厘米,正好变成一个平行四边形,这时面积增加15平方厘米,原来的梯形面积是( )平方厘米。
11.如右图,按照这样的规律排列下去,第六个点阵中点的个数是( )。
12.用小棒按照如下的方式摆图形。
摆1个八边形需要8根小棒,摆2个八边形需要15根小棒,……,摆50个八边形需要( )根小棒;如果摆这样的八边形用了267根小棒,你知道摆了( )个八边形。
13.如图阴影部分是( )形,它的底等于小正方形的( ),高等于大正方形的( ),小正方形边长4cm,大正方形边长6cm,阴影部分面积是( )cm2。
二、选择题。(共20分)
1.能拼成一个平行四边形的两个三角形必须具备( )。
A.面积相等 B.形状相同 C.完全一样 D.任意两个均可
2.如图中,三角形AOD和三角形BOC的面积相比,( )大。
A.三角形AOD B.一样
C.三角形BOC D.无法比较
3.如果两个三角形的面积相等,则这两个三角形( )。
A.形状完全相同 B.底和高相等 C.底和高的乘积相等
4.甲、乙两个三角形面积相等,甲的底边是乙的2倍,甲底边上的高是乙对应底边上高的( )。
A.2倍 B. C.相等 D.无法确定
5.梯形的面积是48平方厘米,高是8厘米,则上、下底的和是( )厘米。
A.12 B.6 C.24
6.面积为15公顷的长方形鱼塘,宽是300米,长是( )米
A.50 B.500 C.5
7.一个教室的长为8米,宽为6米,大约( )个这样的教室面积约1公顷。
A.10 B.200 C.2000
8.阴影部分的面积与其他阴影部分的面积不相等的是( )。
9.李丽参加奥运知识竞赛,竞赛规定,答对一题加10分,答错一题扣5分。李丽答了8道题,得了50分。她答对了( )道题。
A.5 B.6 C.7 D.8
10.如图阴影部分的面积是( )。
A.42cm2 B.36cm2
C.48cm2 D.56cm2
三、判断题。(共5分)
1.一个梯形可以分割成一个平行四边形和一个三角形。( )
2.两个面积相等的三角形,一定可以拼成一个平行四边形。( )
3.两个直角三角形,三条边的长分别是3厘米、4厘米、5厘米。用这两个图形拼成的平行四边形,周长一定是16厘米。( )
4.两个等底等高的三角形,面积相等,但形状不一定相同。( )
5.一个平行四边形的底扩大3.5倍,高不变,则面积扩大3.5倍。( )
四、求下面图形的面积(共27分)
1.估计下面图形的面积。(每个小方格的边长表示1cm)(6分)
2.画出和已知图形面积相等的直角三角形,并写出高的计算过程。(每个正方形的面积为1cm2)(3分)
3.计算下列组合图形的面积。(单位:cm)(9分)
4.求下列阴影部分的面积。(单位:m)(9分)
(1) (2)
(3)平行四边形的面积是32平方分米,求阴影部分的面积。
五、解决问题。(共24分)
1.向阳小学要油漆20扇教室门的外面(如图)。那么需要油漆的面积是多少平方米?(4分)
2.有一个长25米、宽20米的花坛,如果在这个花坛的四周修3米宽的小路(如图),小路的面积是多少平方米?(4分)
3.一块长方形草地,长是15米,宽是10米,中间铺一条石子路(如图)。草地部分面积有多大?(4分)
4.小明家一面外墙墙皮脱落,要重新粉刷,每平方米需要用0.6千克涂料。如果涂料的价格是每千克12元,粉刷这面墙需要多少元?(4分)
5.在一个停车场上,停了汽车和摩托车一共32辆。其中汽车有4个轮子,摩托车有2个轮子,这些车一共有88个轮子。求汽车和摩托车各有多少辆?(4分)
6.一个三角形的底长5m,如果底延长1m,高不变,那么面积就增加1.5m2(如图),原来三角形的面积是多少平方米?(4分)
参考答案
第六单元测试卷
一、1.49.5厘米2 2.1470cm2 3.完全相同
4.640 61.7 0.007 0.75 0.8 5.= > > > 6.12
7.48 8.3.6 9.8 10.65
11.21 12.351 38 13.三角 边长 边长 12
二、1.C 2.B 3.C 4.B 5.A
6.B 7.B 8.D 9.B 10.A
三、1.√
2.× 解析:两个完全相同的三角形,一定可以拼成一个平行四边形。
3.× 解析:周长可以是14cm。
4.√
5.√
四、1.略 2.略
3.(1)30×60-[(30×15)÷2]=1800-225=1575(cm2)
(2)20×16-[(3+9)×5÷2]=320-30=290(cm2)
(3)52×22÷2+[(2+31)×48÷2]=572+792=1364(cm2)
4.(1)24×36-[(18+32)×18÷2]=864-450=414(m2)
(2)(5×5÷2-5×3÷2)×2=10(m2)
(3)高:32÷8=4(dm) 3×4÷2=6(dm2)
五、1.0.8×2=1.6(m2) 0.3×0.4=0.12(m2) (1.6-0.12)×20=29.6(m2) 解析:要求油漆20扇教室的门的外面需要油漆的面积,要先求出一扇门的外面需要油漆的面积,我们可以运用分割法将图中的一扇门,分割成两部分,一部分是长为2米,宽为0.8米的一个大长方形;另一部分是门上的小窗,长为0.4米,宽为0.3米的小长方形,用大长方形的面积减去小长方形的面积即可得到油漆一扇门的外面需要油漆的面积。再用油漆一扇门的面积乘20扇门便可得到一共需要油漆的面积。
2.(25+3×2)×(20+3×2)=806(m2) 25×20=500(m2) 806-500=306(m2) 解析:用外面大长方形的面积减去里面小长方形的面积就等于小路的面积。
3.15×10=150(m2) 1×15=15(m2) 150-15=135(m2) 解析:用大长方形的面积减去里面平行四边形面积=草地部分面积
4.8×3.5+8×2÷2=28+8=36(m2) 36×0.6×12=259.2(元) 解析:先求整面墙的面积=三角形面积+长方形的面积,总价=涂料的数量×单价。
5.假设全部都是汽车,那么轮子就有32×4=128(个) 摩托车:(128-88)÷(4-2)=20(辆) 汽车:32-20=12(辆)
6.高:1.5×2÷1=3(m) 5×3÷2=7.5(m2) 解析:要求原来三角形的面积,先求三角形的高,根据阴影部分面积和底求高:1.5×2÷1=3(m),再求原来三角形的面积:5×3÷2=7.5(m2)。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
