人教版九年级数学上册24.1.3 弧、弦、圆心角 优秀公开课课件(共16张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.3 弧、弦、圆心角 优秀公开课课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第二十四章 圆
24.1.3 弧、弦、圆心角
人教版 数学 九年级 上册
学习目标:
1.理解圆心角的概念,掌握圆的旋转不变性(中心对称性)。
2.掌握圆心角、弧、弦之间的相等关系定理及推论,并初步学会 运用这些关系进行有关的近似和证明。
3.经历动手操作、观察、比较、猜想、推论、归纳等活动观察, 发展推论、概括能力。
1、什么是弦?
连接圆上任意两点的线段叫做弦。
即:如右图弦AB
2、什么是弧?什么是等弧?
.
O
A
B
圆上︵任意两点间的部分叫作圆弧,简称弧,即:如上
图 AB ;在同圆或等圆中,能够互相重合的弧叫做等弧。
O
.
A
B
3-5
我们把顶点在圆心上,角的两边与圆周相交的角 叫做圆心角。
︵
如图3-5所示,∠AOB叫作圆心角, AB 叫作圆
心角∠AOB所对的弧。
探究新知:
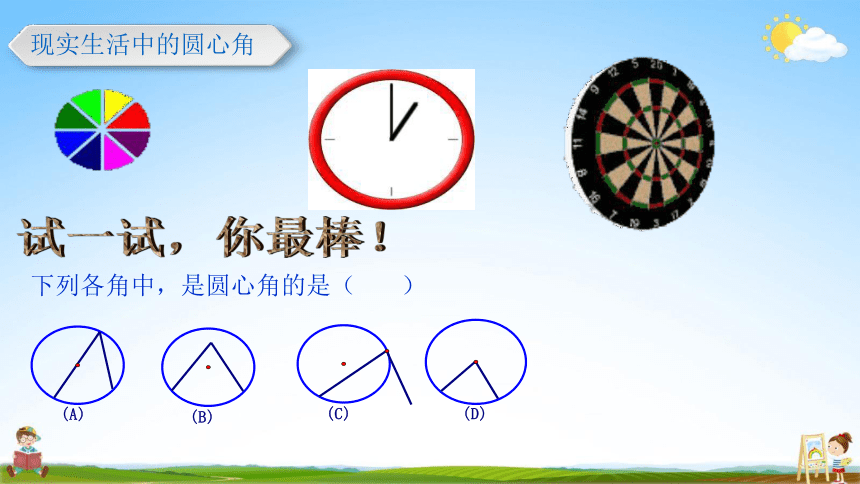
下列各角中,是圆心角的是( )
(D)
(C)
(B)
(A)
现实生活中的圆心角
o .
D
B
A
.
如图所示圆心角∠AOB=∠COD。 它
︵
CD
︵
AB
们所对的弧
与
相等吗?它们所对的弦
AB与CD相等吗?
从而得到下述弧、弦、圆心角三者关系:
在同圆或等圆中,如果圆心角相等,那
那么它们所对的弧相等,所对的弦也相等。
(B)
C
(A)
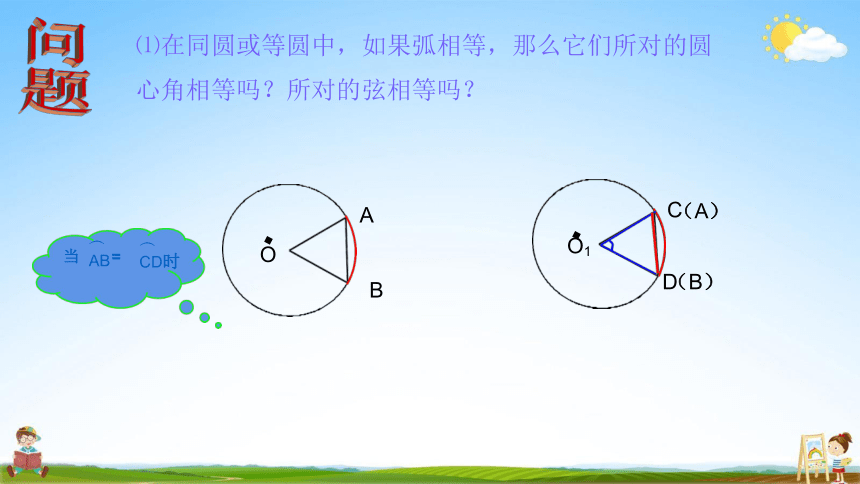
⑴在同圆或等圆中,如果弧相等,那么它们所对的圆 心角相等吗?所对的弦相等吗?
.
A
B
.
O1
O
当
︵
=
AB
︵
CD时
C(A)
D(B)
.
D
C
O
1
.
B
A
O
当AB=CD时
⑵在同圆或等圆中,如果弦相等,那么它们
所对的圆心角相等吗?所对的弧相等吗?
(AB)
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心 角 相等 ,所对的弦 相等。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等 ,所 对的弧 相等 。
在同圆或等圆中,如果两个圆心角、 两条弧、两条弦中有一组量相等,那么它们所对应 的其余各组量也相等。
如图所示,在⊙O中,
∠ACB=60°。
求证:∠AOB=∠BOC=∠AOC
︵
︵
AB= A,C
O
C
B
A
证明:∵
AB
AC
︵ ︵
=
∴AB=AC,△ABC是等腰三角形
(在同圆中,相等的弧所对的弦相等) 又∵∠ACB=60°
∴△ABC是等边三角形,AB=BC=CA
∴∠AOB=∠BOC=∠AOC
(在同圆中,相等的弦所对的圆心角相等)
O
C
B
A
⒈下列命题是真命题的是( )
相等的圆心角所对的弧相等
长度相等的两条弧是等弧
等弦所对的圆心角相等
等弧所对的弦相等
D
, ∠COD=35°,
⒉如图AB是⊙O的直径 求∠AOE的度数。
︵ ︵ ︵
BC = DC = DE
E
D
C
B
O
A
解:∵
=
︵
BC
︵ ︵
DC = DE
∴∠BOC=∠COD=∠DOE
∵∠COD=35°
∴∠BOE=3∠COD=3×35°=105°
∴∠AOE=180°-∠BOE=180°-105°
=75°
⒊如图,已知⊙O中,弦AB=CD
求证:AD=BC
O
D
C
B
A
证明:∵AB=CD =
︵
AB
︵
CD
∴
=
︵ 即: AD
︵
BC
∴
︵
AB
︵
BD
-
=
︵
CD
︵
BD
-
∴AD=BC
(
)
在同圆中,相等的弦所对的弧相等
(在同圆中,相等的弧所对的弦相等)
有一组量相等,那么其余各组量也 。
相等
新知小结:
1、顶点在 圆心上 的角叫做圆心角。
2、在 同圆或等圆 中,相等的圆心
角所对的弦 相等 ,所对的弧 相等 。
3、在同圆或等圆中,如果两条弧、两条弦、两个圆心角中
谢谢观看
Thank You
第二十四章 圆
24.1.3 弧、弦、圆心角
人教版 数学 九年级 上册
学习目标:
1.理解圆心角的概念,掌握圆的旋转不变性(中心对称性)。
2.掌握圆心角、弧、弦之间的相等关系定理及推论,并初步学会 运用这些关系进行有关的近似和证明。
3.经历动手操作、观察、比较、猜想、推论、归纳等活动观察, 发展推论、概括能力。
1、什么是弦?
连接圆上任意两点的线段叫做弦。
即:如右图弦AB
2、什么是弧?什么是等弧?
.
O
A
B
圆上︵任意两点间的部分叫作圆弧,简称弧,即:如上
图 AB ;在同圆或等圆中,能够互相重合的弧叫做等弧。
O
.
A
B
3-5
我们把顶点在圆心上,角的两边与圆周相交的角 叫做圆心角。
︵
如图3-5所示,∠AOB叫作圆心角, AB 叫作圆
心角∠AOB所对的弧。
探究新知:
下列各角中,是圆心角的是( )
(D)
(C)
(B)
(A)
现实生活中的圆心角
o .
D
B
A
.
如图所示圆心角∠AOB=∠COD。 它
︵
CD
︵
AB
们所对的弧
与
相等吗?它们所对的弦
AB与CD相等吗?
从而得到下述弧、弦、圆心角三者关系:
在同圆或等圆中,如果圆心角相等,那
那么它们所对的弧相等,所对的弦也相等。
(B)
C
(A)
⑴在同圆或等圆中,如果弧相等,那么它们所对的圆 心角相等吗?所对的弦相等吗?
.
A
B
.
O1
O
当
︵
=
AB
︵
CD时
C(A)
D(B)
.
D
C
O
1
.
B
A
O
当AB=CD时
⑵在同圆或等圆中,如果弦相等,那么它们
所对的圆心角相等吗?所对的弧相等吗?
(AB)
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心 角 相等 ,所对的弦 相等。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等 ,所 对的弧 相等 。
在同圆或等圆中,如果两个圆心角、 两条弧、两条弦中有一组量相等,那么它们所对应 的其余各组量也相等。
如图所示,在⊙O中,
∠ACB=60°。
求证:∠AOB=∠BOC=∠AOC
︵
︵
AB= A,C
O
C
B
A
证明:∵
AB
AC
︵ ︵
=
∴AB=AC,△ABC是等腰三角形
(在同圆中,相等的弧所对的弦相等) 又∵∠ACB=60°
∴△ABC是等边三角形,AB=BC=CA
∴∠AOB=∠BOC=∠AOC
(在同圆中,相等的弦所对的圆心角相等)
O
C
B
A
⒈下列命题是真命题的是( )
相等的圆心角所对的弧相等
长度相等的两条弧是等弧
等弦所对的圆心角相等
等弧所对的弦相等
D
, ∠COD=35°,
⒉如图AB是⊙O的直径 求∠AOE的度数。
︵ ︵ ︵
BC = DC = DE
E
D
C
B
O
A
解:∵
=
︵
BC
︵ ︵
DC = DE
∴∠BOC=∠COD=∠DOE
∵∠COD=35°
∴∠BOE=3∠COD=3×35°=105°
∴∠AOE=180°-∠BOE=180°-105°
=75°
⒊如图,已知⊙O中,弦AB=CD
求证:AD=BC
O
D
C
B
A
证明:∵AB=CD =
︵
AB
︵
CD
∴
=
︵ 即: AD
︵
BC
∴
︵
AB
︵
BD
-
=
︵
CD
︵
BD
-
∴AD=BC
(
)
在同圆中,相等的弦所对的弧相等
(在同圆中,相等的弧所对的弦相等)
有一组量相等,那么其余各组量也 。
相等
新知小结:
1、顶点在 圆心上 的角叫做圆心角。
2、在 同圆或等圆 中,相等的圆心
角所对的弦 相等 ,所对的弧 相等 。
3、在同圆或等圆中,如果两条弧、两条弦、两个圆心角中
谢谢观看
Thank You
同课章节目录
