人教版九年级数学上册24.1.4 圆内接四边形 教学课件(共26张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.4 圆内接四边形 教学课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-12 18:31:09 | ||
图片预览


文档简介
(共26张PPT)
第二十四章 圆
24.1.4 圆内接四边形
人教版 数学 九年级 上册
学习目标:
理解圆内接四边形和多边形的外接圆的概念,掌握圆内接四边 形的性质,并会用此性质进行有关的计算和证明。
进一步掌握圆周角定理及推论,并会综合运用知识进行有关的 计算和证明。
学习中注重培养自己的逻辑思维能力、分析、解决问题能力。
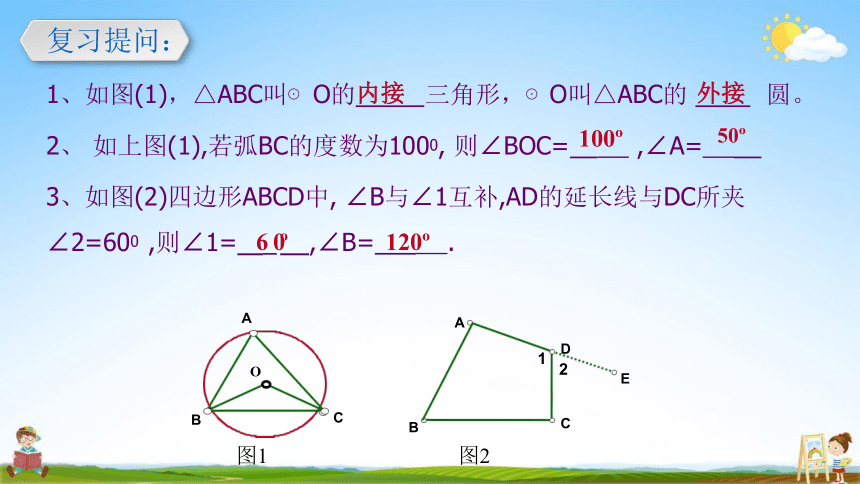
复习提问:
A
B
C
E
D
C
B
A
2
1
图1
图2
O
1、如图(1),△ABC叫⊙ O的内接 三角形,⊙ O叫△ABC的 外接 圆。
2、 如上图(1),若弧BC的度数为1000, 则∠BOC= 100 ,∠A=
50
3、如图(2)四边形ABCD中, ∠B与∠1互补,AD的延长线与DC所夹
∠2=600 ,则∠1= 6_0 ,∠B= 120 .
O
C
A
B
D
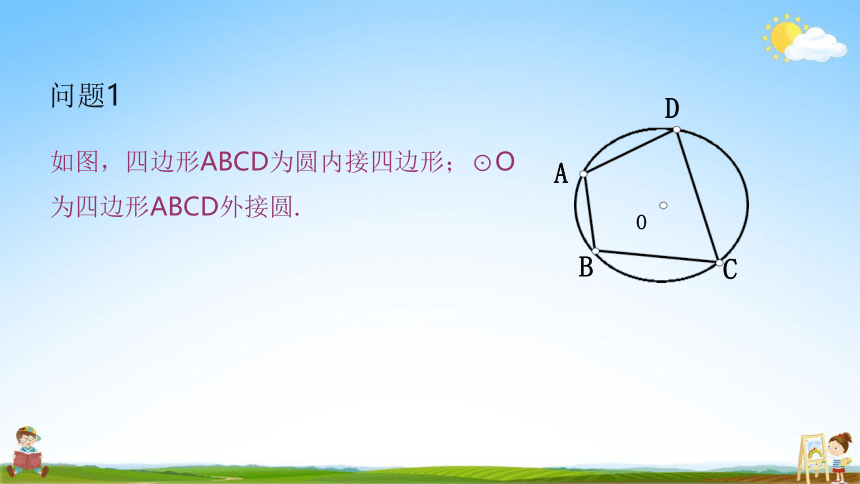
如图,四边形ABCD为圆内接四边形;⊙O 为四边形ABCD外接圆.
问题1
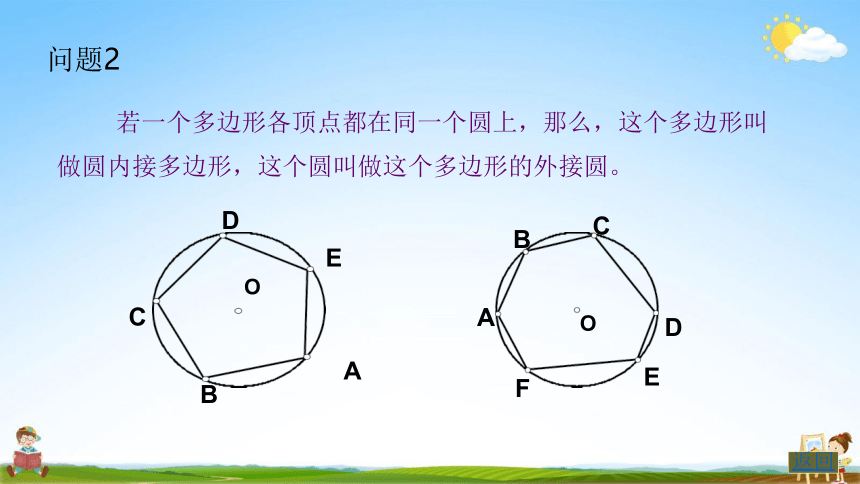
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫 做圆内接多边形,这个圆叫做这个多边形的外接圆。
O
B
C
D
E
F
A
O
A
C
D
E
B
返回
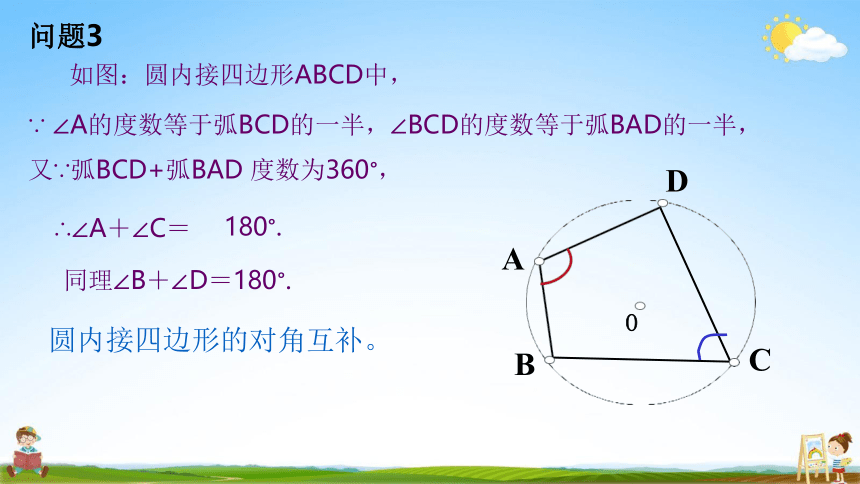
问题2
C
O
D
B
A
又∵弧BCD+弧BAD 度数为360°,
∴∠A+∠C=
180°.
同理∠B+∠D=180°.
圆内接四边形的对角互补。
问题3
如图:圆内接四边形ABCD中,
∵ ∠A的度数等于弧BCD的一半,∠BCD的度数等于弧BAD的一半,
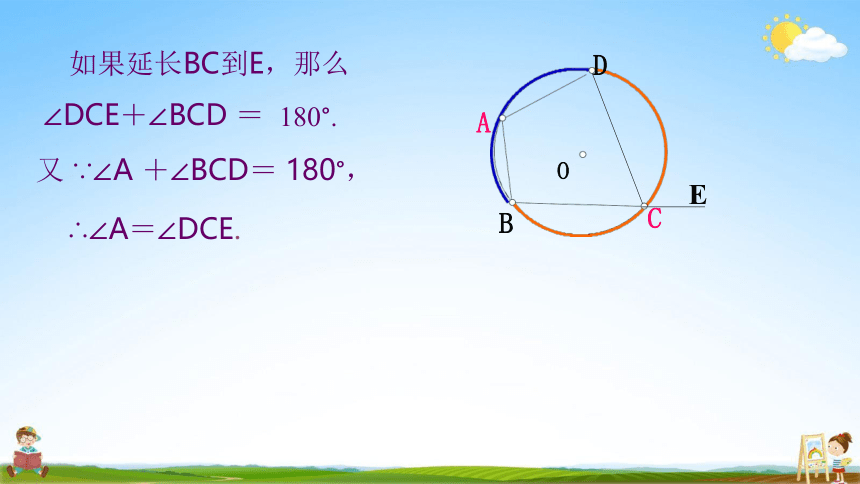
如果延长BC到E,那么
∠DCE+∠BCD = 180°.
又 ∵∠A +∠BCD= 180°,
∴∠A=∠DCE.
C
O
D
B
A
E
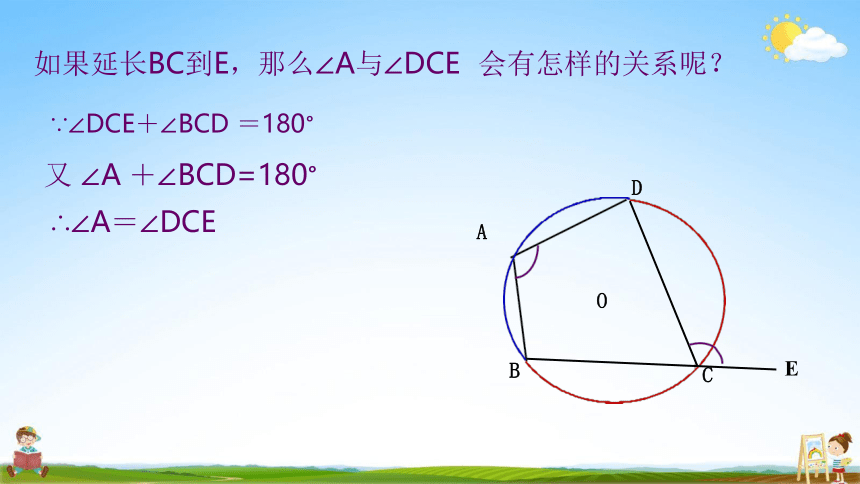
如果延长BC到E,那么∠A与∠DCE 会有怎样的关系呢?
A
E
C
O
D
B
又 ∠A +∠BCD=180°
∴∠A=∠DCE
∵∠DCE+∠BCD =180°
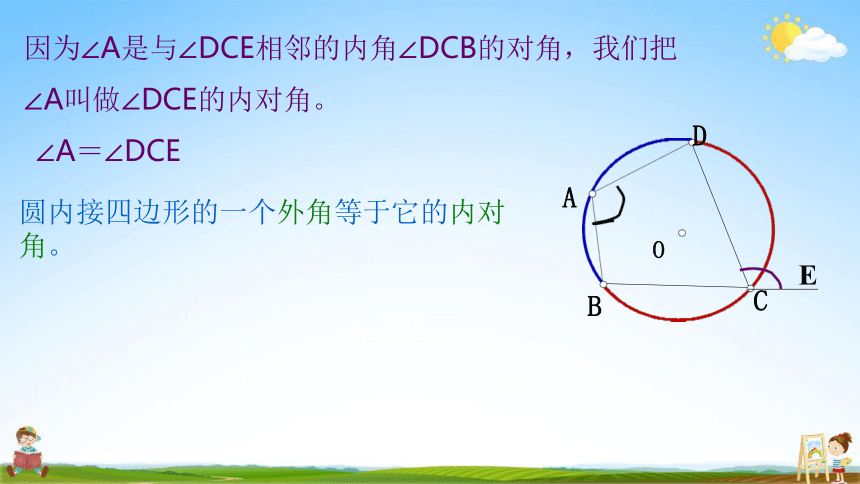
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把
圆内接四边形的一个外角等于它的内对 角。
C
O
D
B
A
E
∠A叫做∠DCE的内对角。
∠A=∠DCE
几何表达式:
∵ 四边形ABCD内接于⊙O,
∴ ∠A+∠C=180°且∠B=∠1 .
A
B
C
D
1
E
探索结论
先根据图形讨论,然后用语言归纳为 :
性质定理: 圆的内接四边形的对角互补,并且任 何一个外角都等于它的内对角。
1
2
O
O
F
A
B
E
C
应用举例
例 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与
⊙O2 交于点F。
D
求证:CE∥DF
CE∥DF
∠E+∠F=180°
∠E+∠1=180°、∠1=∠F
ABEC是⊙O1
的内接四边形
ABFD是⊙O2
的内接四边形
连结AB
1
2
O
O
F
A
B
E
C
D
1
思路分析
反思与拓展
O 2
O 1
B
证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内 错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE
∥ DF,想一想还能否通过同位角相等或者内错角相等证明结果?
方法二 延长EF,是否有∠E=∠BAD= ∠1 ?
D
A
C
E
1
F
M
能否证明∠E=∠2=∠3?
A
2
O 2
3
O 1
B
C
D
E
F
方法三
延长DF,
变式1:如图,⊙O1和⊙O2都经过A、B两点,过A点的直线CD与
⊙O1交于点C,与⊙O2交于点D,过B点的直线EF与⊙O1交于点E, 与⊙O2交于点F。
E
D
A
C
B
F
猜想:CE∥DF仍然成立吗?
O1
O2
变式2:如图,⊙O1和⊙O2有两个公共点A﹑B,过A﹑B两点的直线分 别交⊙O1于C 、E,交⊙O2于D 、F,且CD∥EF。
C
A
B
E
D
F
O1
O2
求证:CE=DF
达标练习
一、填空
四边形ABCD内接于⊙O,则∠A+∠C=_1_80°,
∠B+∠ADC= 180°; 若∠B=800,
则∠ADC=_10_0_°_ ∠CDE=_8_0_° (图1)
四边形ABCD内接于⊙O,∠AOC=1000 则∠B=_5_0_° ∠D=_1_3_0°_(图2)
(3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A= 4_5_°_,
E
B
A
D
C
80
D
B
A
C
O
100
达标练习
图2
图1
D
B
A
C
O
A.菱形 C.正方形
B.矩形
D.等腰梯形
(4)如图3,梯形ABCD内接于⊙O,AD∥BC, ∠B=750, 则∠C= 7_5_°_.
2、选择题:
圆内接平行四边形必为( B )
图3
3、 如图,四边形ABCD为⊙O的内接四边形,已
反馈练习:
A
B
C
D
O
50
知∠BOD=100°,则∠BAD=
∠BCD= 130
4、圆内接四边形ABCD中,∠A:∠B:∠C=
2:3:4,则∠A= ∠B=
∠C=
60 90
120
∠D= 90
5、如图,四边形ABCD内接于⊙O, ∠DCE=75 , 则∠BOD= 150
B
D
O
C A E
本节课所学的内容可概括为三个“1”.
一个概念: 圆的内接四边形;
一个定理:圆的内接四边形的性质定理; 添辅助线的方法:作两圆的公共弦.
课堂小结
1、圆内接四边形------顶点在圆上的四边形,该圆 叫四边形的外接圆。
2、圆内接四边形的性质
外角等于它的内对角
对角互补
3、解题时应注意两点:
注意观察图形,分清四边形的外角和它的内对角的位置, 不要受背景的干扰。
证题时,常需添辅助线-----两圆共有一条弦(公共弦), 构造圆内接四边形。
思维拓展:
3、圆内接菱形一定是
形。
1、圆内接平行四边形一定是 矩 形。
2、圆内接梯形一定是 等腰梯 形。
正方
谢谢观看
Thank You
第二十四章 圆
24.1.4 圆内接四边形
人教版 数学 九年级 上册
学习目标:
理解圆内接四边形和多边形的外接圆的概念,掌握圆内接四边 形的性质,并会用此性质进行有关的计算和证明。
进一步掌握圆周角定理及推论,并会综合运用知识进行有关的 计算和证明。
学习中注重培养自己的逻辑思维能力、分析、解决问题能力。
复习提问:
A
B
C
E
D
C
B
A
2
1
图1
图2
O
1、如图(1),△ABC叫⊙ O的内接 三角形,⊙ O叫△ABC的 外接 圆。
2、 如上图(1),若弧BC的度数为1000, 则∠BOC= 100 ,∠A=
50
3、如图(2)四边形ABCD中, ∠B与∠1互补,AD的延长线与DC所夹
∠2=600 ,则∠1= 6_0 ,∠B= 120 .
O
C
A
B
D
如图,四边形ABCD为圆内接四边形;⊙O 为四边形ABCD外接圆.
问题1
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫 做圆内接多边形,这个圆叫做这个多边形的外接圆。
O
B
C
D
E
F
A
O
A
C
D
E
B
返回
问题2
C
O
D
B
A
又∵弧BCD+弧BAD 度数为360°,
∴∠A+∠C=
180°.
同理∠B+∠D=180°.
圆内接四边形的对角互补。
问题3
如图:圆内接四边形ABCD中,
∵ ∠A的度数等于弧BCD的一半,∠BCD的度数等于弧BAD的一半,
如果延长BC到E,那么
∠DCE+∠BCD = 180°.
又 ∵∠A +∠BCD= 180°,
∴∠A=∠DCE.
C
O
D
B
A
E
如果延长BC到E,那么∠A与∠DCE 会有怎样的关系呢?
A
E
C
O
D
B
又 ∠A +∠BCD=180°
∴∠A=∠DCE
∵∠DCE+∠BCD =180°
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把
圆内接四边形的一个外角等于它的内对 角。
C
O
D
B
A
E
∠A叫做∠DCE的内对角。
∠A=∠DCE
几何表达式:
∵ 四边形ABCD内接于⊙O,
∴ ∠A+∠C=180°且∠B=∠1 .
A
B
C
D
1
E
探索结论
先根据图形讨论,然后用语言归纳为 :
性质定理: 圆的内接四边形的对角互补,并且任 何一个外角都等于它的内对角。
1
2
O
O
F
A
B
E
C
应用举例
例 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与
⊙O2 交于点F。
D
求证:CE∥DF
CE∥DF
∠E+∠F=180°
∠E+∠1=180°、∠1=∠F
ABEC是⊙O1
的内接四边形
ABFD是⊙O2
的内接四边形
连结AB
1
2
O
O
F
A
B
E
C
D
1
思路分析
反思与拓展
O 2
O 1
B
证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内 错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE
∥ DF,想一想还能否通过同位角相等或者内错角相等证明结果?
方法二 延长EF,是否有∠E=∠BAD= ∠1 ?
D
A
C
E
1
F
M
能否证明∠E=∠2=∠3?
A
2
O 2
3
O 1
B
C
D
E
F
方法三
延长DF,
变式1:如图,⊙O1和⊙O2都经过A、B两点,过A点的直线CD与
⊙O1交于点C,与⊙O2交于点D,过B点的直线EF与⊙O1交于点E, 与⊙O2交于点F。
E
D
A
C
B
F
猜想:CE∥DF仍然成立吗?
O1
O2
变式2:如图,⊙O1和⊙O2有两个公共点A﹑B,过A﹑B两点的直线分 别交⊙O1于C 、E,交⊙O2于D 、F,且CD∥EF。
C
A
B
E
D
F
O1
O2
求证:CE=DF
达标练习
一、填空
四边形ABCD内接于⊙O,则∠A+∠C=_1_80°,
∠B+∠ADC= 180°; 若∠B=800,
则∠ADC=_10_0_°_ ∠CDE=_8_0_° (图1)
四边形ABCD内接于⊙O,∠AOC=1000 则∠B=_5_0_° ∠D=_1_3_0°_(图2)
(3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A= 4_5_°_,
E
B
A
D
C
80
D
B
A
C
O
100
达标练习
图2
图1
D
B
A
C
O
A.菱形 C.正方形
B.矩形
D.等腰梯形
(4)如图3,梯形ABCD内接于⊙O,AD∥BC, ∠B=750, 则∠C= 7_5_°_.
2、选择题:
圆内接平行四边形必为( B )
图3
3、 如图,四边形ABCD为⊙O的内接四边形,已
反馈练习:
A
B
C
D
O
50
知∠BOD=100°,则∠BAD=
∠BCD= 130
4、圆内接四边形ABCD中,∠A:∠B:∠C=
2:3:4,则∠A= ∠B=
∠C=
60 90
120
∠D= 90
5、如图,四边形ABCD内接于⊙O, ∠DCE=75 , 则∠BOD= 150
B
D
O
C A E
本节课所学的内容可概括为三个“1”.
一个概念: 圆的内接四边形;
一个定理:圆的内接四边形的性质定理; 添辅助线的方法:作两圆的公共弦.
课堂小结
1、圆内接四边形------顶点在圆上的四边形,该圆 叫四边形的外接圆。
2、圆内接四边形的性质
外角等于它的内对角
对角互补
3、解题时应注意两点:
注意观察图形,分清四边形的外角和它的内对角的位置, 不要受背景的干扰。
证题时,常需添辅助线-----两圆共有一条弦(公共弦), 构造圆内接四边形。
思维拓展:
3、圆内接菱形一定是
形。
1、圆内接平行四边形一定是 矩 形。
2、圆内接梯形一定是 等腰梯 形。
正方
谢谢观看
Thank You
同课章节目录
