人教版九年级数学上册24.4 弧长和扇形面积 教学课件PPT优秀公开课(16张ppt)
文档属性
| 名称 | 人教版九年级数学上册24.4 弧长和扇形面积 教学课件PPT优秀公开课(16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 07:59:47 | ||
图片预览




文档简介
(共16张PPT)
第二十四章 圆
24.4 弧长和扇形面积
人教版 数学 九年级 上册
学习目标:
1.了解扇形的概念,理解圆心角所对弧长和扇形面积的计算公式 并熟练应用。
2.通过复习圆的周长、圆的面积公式,探索圆心角所对的弧长和 扇形面积的计算公式。
一、情境导入
在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位 运动员所跑弯路的展直长度相不相同呢?
半 径
半径
圆圆心心角角
弧
A
B
O
B
A
扇形
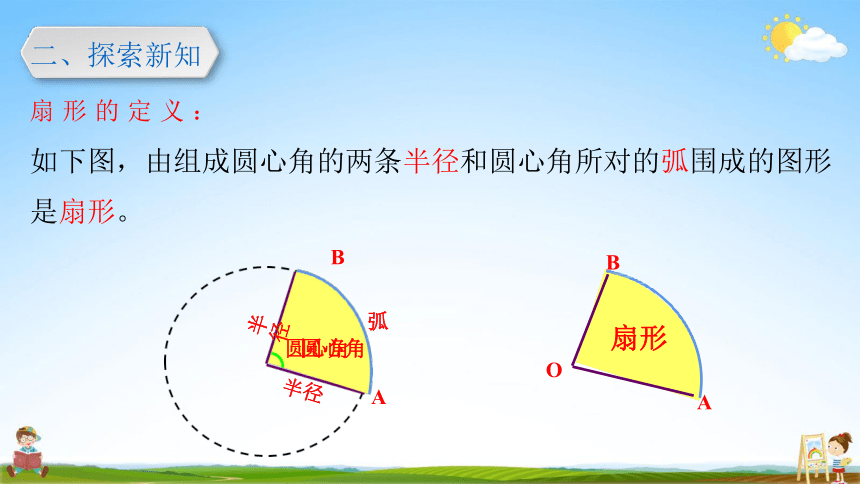
二、探索新知
扇 形 的 定 义 :
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形 是扇形。
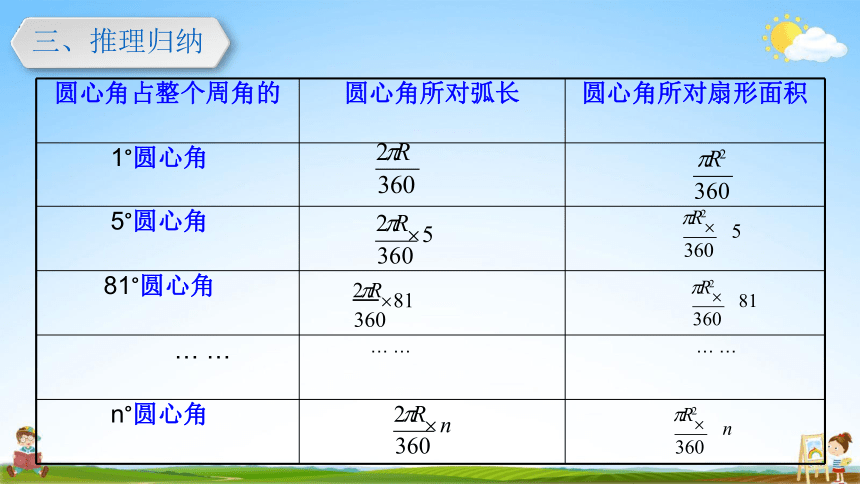
圆心角占整个周角的 圆心角所对弧长 圆心角所对扇形面积
1°圆心角 2 R 360 R2
360
5°圆心角 2 R 5 360 R2
5
360
81°圆心角 2 R 81 R2
81
360
360
… … … … … …
n°圆心角 2 R n 360 R2
n
360
三、推理归纳
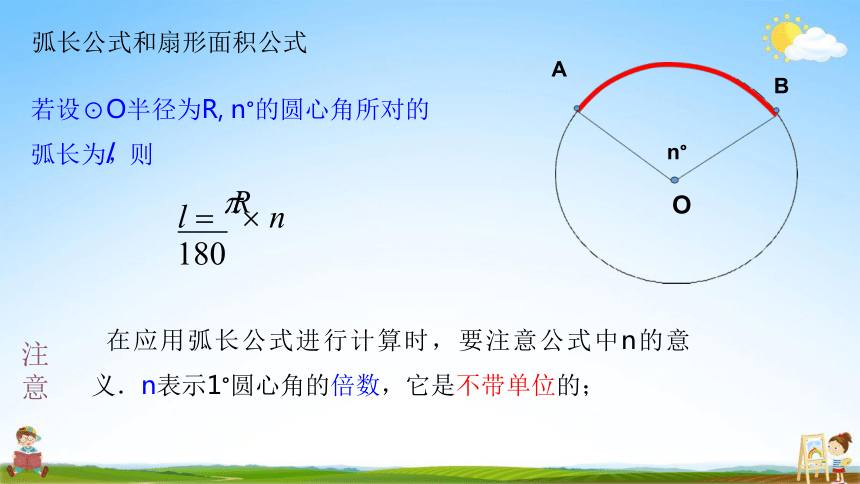
在应用弧长公式进行计算时,要注意公式中n的意 义.n表示1°圆心角的倍数,它是不带单位的;
A
O
B
n°
弧长公式和扇形面积公式
注 意
180
若设⊙O半径为R, n°的圆心角所对的 弧长为l,则
l R n
lR
2
1
R2
S扇形 S圆 360 n
注意
为什么不写成:
nR2
360
nR
180
l
和S
如果用字母 S 表示扇形的面积,n表 示圆心角的度数,R 表示圆半径,那 么扇形面积的计算公式是:
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算 图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
l
180
100 900 500 1570(mm)
因此所要求的展直长度
答:管道的展直长度为2970mm。
四、例题解析
已知一条弧的半径为9,弧长为8π ,那么这条弧所对的圆心角为 16_0°_。
如图,把Rt△ABC的斜边放在直线 I上,按顺时针方向转动一次,使它 转到△A′B C ′的位置。若BC=1,∠A=30 ,求点A运动到A′位置时,点A经 过的路线长。
l
l 4
3
五、试一试
1.已知弧所对的圆心角为900,半径是4,则弧长为 2_
4、已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形=
.
6、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求
图中阴影部分的面积。
3
B
A
C
D
3
4
5、已知扇形面积为1 ,圆心角为30°,则这个扇形的半径R=_2 .
S=4π
一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),
●
B
B2
B1
B
BC
DE
FB2
那么B点从开始至B2结束所走过的路径长度 3 .
B1
l 4
六、我也创新
如图,一根 5m 长的绳 子,一端栓在柱子上,另 一端栓着一只羊, 羊的 活动最大区域是多少? 请同学们画图说明.
5
柱子
生活中的数学
5m
o
4m
5m
o
4m
(A)
(B)
(C)
2.探索弧长及扇形的面积之间的关系,并能已知l、n、R、S中 的两个量求另一两个量.
1.探索弧长公式.
l 2 R n Rn
360 180
360 360 2
n lR
S
R2 nR2 1
课堂小结
作业:
1.课本第113页练习:1、2、3题.
2.课本第115页习题:1题(1)、(2).
谢谢观看
Thank You
第二十四章 圆
24.4 弧长和扇形面积
人教版 数学 九年级 上册
学习目标:
1.了解扇形的概念,理解圆心角所对弧长和扇形面积的计算公式 并熟练应用。
2.通过复习圆的周长、圆的面积公式,探索圆心角所对的弧长和 扇形面积的计算公式。
一、情境导入
在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位 运动员所跑弯路的展直长度相不相同呢?
半 径
半径
圆圆心心角角
弧
A
B
O
B
A
扇形
二、探索新知
扇 形 的 定 义 :
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形 是扇形。
圆心角占整个周角的 圆心角所对弧长 圆心角所对扇形面积
1°圆心角 2 R 360 R2
360
5°圆心角 2 R 5 360 R2
5
360
81°圆心角 2 R 81 R2
81
360
360
… … … … … …
n°圆心角 2 R n 360 R2
n
360
三、推理归纳
在应用弧长公式进行计算时,要注意公式中n的意 义.n表示1°圆心角的倍数,它是不带单位的;
A
O
B
n°
弧长公式和扇形面积公式
注 意
180
若设⊙O半径为R, n°的圆心角所对的 弧长为l,则
l R n
lR
2
1
R2
S扇形 S圆 360 n
注意
为什么不写成:
nR2
360
nR
180
l
和S
如果用字母 S 表示扇形的面积,n表 示圆心角的度数,R 表示圆半径,那 么扇形面积的计算公式是:
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算 图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
l
180
100 900 500 1570(mm)
因此所要求的展直长度
答:管道的展直长度为2970mm。
四、例题解析
已知一条弧的半径为9,弧长为8π ,那么这条弧所对的圆心角为 16_0°_。
如图,把Rt△ABC的斜边放在直线 I上,按顺时针方向转动一次,使它 转到△A′B C ′的位置。若BC=1,∠A=30 ,求点A运动到A′位置时,点A经 过的路线长。
l
l 4
3
五、试一试
1.已知弧所对的圆心角为900,半径是4,则弧长为 2_
4、已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形=
.
6、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求
图中阴影部分的面积。
3
B
A
C
D
3
4
5、已知扇形面积为1 ,圆心角为30°,则这个扇形的半径R=_2 .
S=4π
一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),
●
B
B2
B1
B
BC
DE
FB2
那么B点从开始至B2结束所走过的路径长度 3 .
B1
l 4
六、我也创新
如图,一根 5m 长的绳 子,一端栓在柱子上,另 一端栓着一只羊, 羊的 活动最大区域是多少? 请同学们画图说明.
5
柱子
生活中的数学
5m
o
4m
5m
o
4m
(A)
(B)
(C)
2.探索弧长及扇形的面积之间的关系,并能已知l、n、R、S中 的两个量求另一两个量.
1.探索弧长公式.
l 2 R n Rn
360 180
360 360 2
n lR
S
R2 nR2 1
课堂小结
作业:
1.课本第113页练习:1、2、3题.
2.课本第115页习题:1题(1)、(2).
谢谢观看
Thank You
同课章节目录
