江苏省沭阳高级中学2012-2013学年高一上学期期中考试数学试题
文档属性
| 名称 | 江苏省沭阳高级中学2012-2013学年高一上学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 223.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-12 15:03:37 | ||
图片预览


文档简介
沭阳高级中学2012-2013学年高一上学期期中考试数学试题
一、填空题(5分×14=70分)
1
2
3
4
4
3
1
2
第2题表
1.设集合,,则= ▲ .
2.已知映射由右表给出,则 ▲ .
3.满足集合,则集合的个数为 ▲ .
4.若函数为奇函数,则 ▲ .
5.如图所示的图中,,是非空集合,定义集合#
为阴影部分表示的集合.若, ,
,则#= ▲ .
6.某班46名学生中,有篮球爱好者23人,足球爱好者29人,
同时爱好这两项运动的人最多有人,最少有人,则= ▲ .
7.设,若幂函数为偶函数且在上单调递减,
则 ▲ .
8.设集合,集合.若点,则
▲ .
9.设则由小到大的顺序是 ▲ .
10.已知函数的图象如图所示,则 ▲ .
11.在使用二分法求方程的近似解过程中,已确定方程
一根,则再经过两次计算后,所在的开区间为 ▲ .
12.函数在上的最大值与最小值之
和为,则的值为 ▲ .
13.函数的值域为 ▲ .
14.已知函数,若在区间上的最大值为1,则的取
值范围为 ▲ .
二、解答题(解答题应写出必要的文字说明,证明过程或演算步骤)
15.(14分)已知全集,函数的定义域为集合,集合=<<.
(1)求集合; (2)若,求的取值范围.
16.(14分)计算下列各式的值:
(1)设,求的值;
(2).
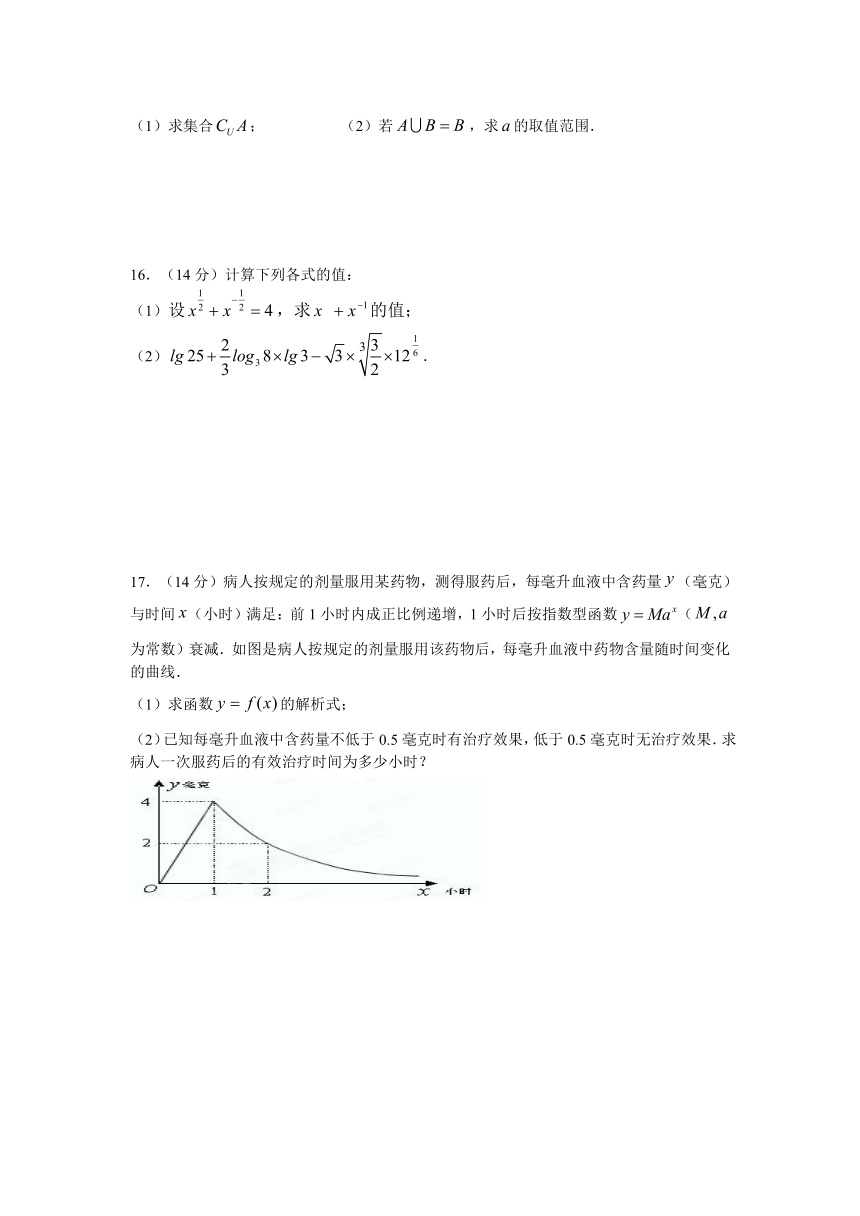
17.(14分)病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量(毫克)与时间(小时)满足:前1小时内成正比例递增,1小时后按指数型函数(为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?
18.(16分)已知二次函数的图像关于直线对称,且在轴上截得的线段长为2.若的最小值为,求:
(1)函数的解析式;
(2)函数在上的最小值.
19.(16分)已知函数是定义在上的奇函数,且当时,.
(1)当时,求函数的解析式;
(2)若函数为单调递减函数;
①直接写出的范围(不必证明);
②若对任意实数,恒成立,求实数的取值范围.
20.(16分)已知函数
(1)求证:函数在上为单调增函数;
(2)设,求的值域;
(3)对于(2)中函数,若关于的方程有三个不同的实数解,求的取值范围.
2012~2013学年度第一学高一年级期中调研测试
数学参考答案
一、填空题(5分×14=70分)
二、解答题(解答题应写出必要的文字说明,证明过程或演算步骤)
15.答案:
(1)因为集合表示的定义域,
所以,即 …………………………6分
所以= …………………………8分
(2)因为 , 所以 …………………………12分
∴≥3 …………………………14分
16.答案:(1)因为 所以
即; 则 …………………………7分
…………………………14分
17.答案:
(1)当时,与成正比例,设为,
又过(1,4)点, ∴∴, …………………………2分
当时,,又过(1,4)、(2,2)点,
所以, 所以 所以 …………6分
所以 …………………………8分
则当时,有治疗效果
所以有效治疗时间为小时 …………………………14分
(或解方程,再求两根差)
18.答案:
(1)因为的对称轴为,的最小值为,
所以的顶点为,
所以的解析式可设为, ………………4分
(2)当即时, ……………………10分
当即时, ……………………12分
当时, ……………………14分
综上得 ……………………16分
19.答案:
(1)当时,,又因为为奇函数,
所以
所以 …………………………6分
(2)①当时,对称轴,所以在上单调递减,
由于奇函数关于原点对称的区间上单调性相同,所以在上单调递减,
又在上,在上,
②因为,∴
所以是奇函数,∴ …………………………12分
又因为为上的单调递减函数,所以恒成立,…………………14分
所以恒成立, 所以 …………………………16分
20.答案:
(1),设是上的任意两个数,且,……2分
则……4分
因为,∴,∴即
所以在上为增函数, …………………………6分
(2),
因为,所以,所以,
即 …………………………8分
又因为时,单调递增,单调递增,
所以单调递增,所以值域为 …………………………10分
(3)由(2)可知大致图象如右图所示,
设,则有三个不同的实数解,即为有两个根,且一个在上,一个在上,设 ………12分
①当有一个根为1时,
,,此时另一根为适合题意; ………………13分
②当没有根为1时,,得,∴
∴的取值范围为 …………………………16分
一、填空题(5分×14=70分)
1
2
3
4
4
3
1
2
第2题表
1.设集合,,则= ▲ .
2.已知映射由右表给出,则 ▲ .
3.满足集合,则集合的个数为 ▲ .
4.若函数为奇函数,则 ▲ .
5.如图所示的图中,,是非空集合,定义集合#
为阴影部分表示的集合.若, ,
,则#= ▲ .
6.某班46名学生中,有篮球爱好者23人,足球爱好者29人,
同时爱好这两项运动的人最多有人,最少有人,则= ▲ .
7.设,若幂函数为偶函数且在上单调递减,
则 ▲ .
8.设集合,集合.若点,则
▲ .
9.设则由小到大的顺序是 ▲ .
10.已知函数的图象如图所示,则 ▲ .
11.在使用二分法求方程的近似解过程中,已确定方程
一根,则再经过两次计算后,所在的开区间为 ▲ .
12.函数在上的最大值与最小值之
和为,则的值为 ▲ .
13.函数的值域为 ▲ .
14.已知函数,若在区间上的最大值为1,则的取
值范围为 ▲ .
二、解答题(解答题应写出必要的文字说明,证明过程或演算步骤)
15.(14分)已知全集,函数的定义域为集合,集合=<<.
(1)求集合; (2)若,求的取值范围.
16.(14分)计算下列各式的值:
(1)设,求的值;
(2).
17.(14分)病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量(毫克)与时间(小时)满足:前1小时内成正比例递增,1小时后按指数型函数(为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?
18.(16分)已知二次函数的图像关于直线对称,且在轴上截得的线段长为2.若的最小值为,求:
(1)函数的解析式;
(2)函数在上的最小值.
19.(16分)已知函数是定义在上的奇函数,且当时,.
(1)当时,求函数的解析式;
(2)若函数为单调递减函数;
①直接写出的范围(不必证明);
②若对任意实数,恒成立,求实数的取值范围.
20.(16分)已知函数
(1)求证:函数在上为单调增函数;
(2)设,求的值域;
(3)对于(2)中函数,若关于的方程有三个不同的实数解,求的取值范围.
2012~2013学年度第一学高一年级期中调研测试
数学参考答案
一、填空题(5分×14=70分)
二、解答题(解答题应写出必要的文字说明,证明过程或演算步骤)
15.答案:
(1)因为集合表示的定义域,
所以,即 …………………………6分
所以= …………………………8分
(2)因为 , 所以 …………………………12分
∴≥3 …………………………14分
16.答案:(1)因为 所以
即; 则 …………………………7分
…………………………14分
17.答案:
(1)当时,与成正比例,设为,
又过(1,4)点, ∴∴, …………………………2分
当时,,又过(1,4)、(2,2)点,
所以, 所以 所以 …………6分
所以 …………………………8分
则当时,有治疗效果
所以有效治疗时间为小时 …………………………14分
(或解方程,再求两根差)
18.答案:
(1)因为的对称轴为,的最小值为,
所以的顶点为,
所以的解析式可设为, ………………4分
(2)当即时, ……………………10分
当即时, ……………………12分
当时, ……………………14分
综上得 ……………………16分
19.答案:
(1)当时,,又因为为奇函数,
所以
所以 …………………………6分
(2)①当时,对称轴,所以在上单调递减,
由于奇函数关于原点对称的区间上单调性相同,所以在上单调递减,
又在上,在上,
②因为,∴
所以是奇函数,∴ …………………………12分
又因为为上的单调递减函数,所以恒成立,…………………14分
所以恒成立, 所以 …………………………16分
20.答案:
(1),设是上的任意两个数,且,……2分
则……4分
因为,∴,∴即
所以在上为增函数, …………………………6分
(2),
因为,所以,所以,
即 …………………………8分
又因为时,单调递增,单调递增,
所以单调递增,所以值域为 …………………………10分
(3)由(2)可知大致图象如右图所示,
设,则有三个不同的实数解,即为有两个根,且一个在上,一个在上,设 ………12分
①当有一个根为1时,
,,此时另一根为适合题意; ………………13分
②当没有根为1时,,得,∴
∴的取值范围为 …………………………16分
同课章节目录
