人教版数学八年级下册 16.3.1 二次根式的加减2 课件(共28张PPT)
文档属性
| 名称 | 人教版数学八年级下册 16.3.1 二次根式的加减2 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 608.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
(a≥0,b≥0)
(a≥0,b>0)
最简二次根式。
复习回顾
下列根式中,哪些是最简二次根式?
复习回顾
√
×
×
×
×
√
√
×
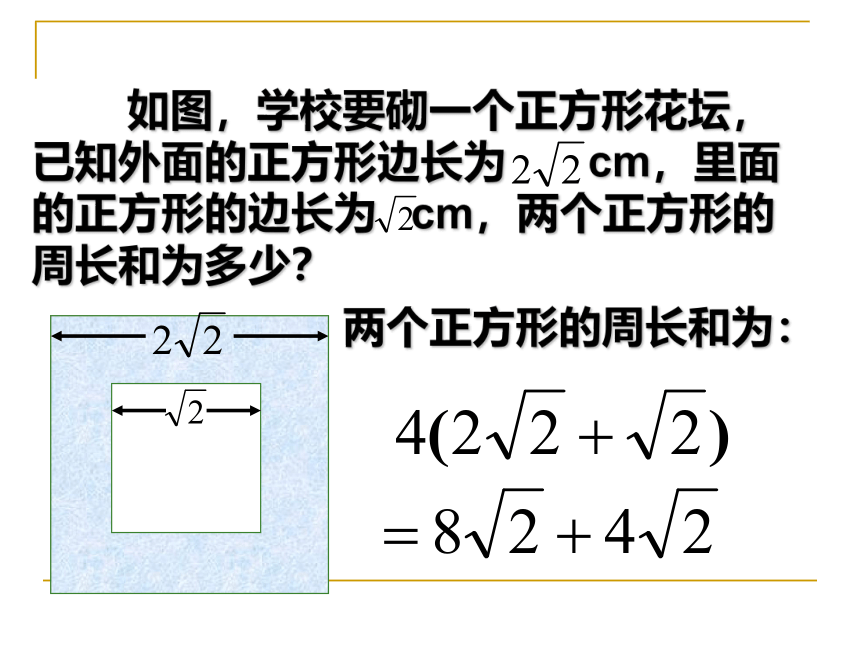
如图,学校要砌一个正方形花坛,已知外面的正方形边长为 cm,里面的正方形的边长为 cm,两个正方形的周长和为多少?
两个正方形的周长和为:
若两个正方形的面积分别为27cm2、12cm2,则两正方形的周长和为多少?
两个正方形的周长和为:
观察
以下是什么运算?如何计算?
二次根式的加法.
如何计算 呢?
分析: 类似8a+4a=12a,我们可以根据乘法分配律的逆用来进行运算。
探究
解:
如何计算 呢?
分析:题中二次根式不是最简二次根式,所以先要对其进行化简。再计算。
解:
讨论
仿照前两题,你能算出这个题吗?
有什么发现?
观察
计算:
有什么发现?
梳理
二次根式加减时,先将二次根式化为最简二次根式,再把被开方数相同的二次根式进行合并。
注意:对被开方数相同的二次根式进行合并,实质是对被开方数相同的二次根式的系数进行合并。
观察
化简:
每组二次根式在化简后有什么特点?
几个二次根式化为最简二次根式后,若被开方数相同,则这几个二次根式就叫做同类二次根式。
梳理
下列各组二次根式是否为同类二次根式?
探究
√
×
√
×
√
如何判断?
判断几个二次根式是否为同类二次根式的方法:
1、先化简:把各个二次根式都化为最简二次根式。
2、再观察:化简后的二次根式的被开方数是否相同。
梳理
例题讲解
1、计算:
解:
2、计算:
加减混合运算,应从左向右依次计算。
探究
解:原式=
别漏了“1”.
化简
解:原式=
下列解答是否正确?为什么?
错在没有按照二次根式加减混算从左向右依次进行的运算顺序计算。
运算不完全,能合并的没有合并。
P16练习1题
P17习题1题
归纳
二次根式的加减与整式的加减根据都是分配律,它们的运算实质也基本相同。
二次根式的加减即为对同类二次根式的合并。
先化为最简二次根式
把同类二次根式合并(合并系数)。
巩固练习
计算:
(3)合并同类二次根式。
一化
二找
三合并
二次根式加减法的步骤:
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
交流 归纳
(a≥0,b≥0)
(a≥0,b>0)
最简二次根式。
复习回顾
下列根式中,哪些是最简二次根式?
复习回顾
√
×
×
×
×
√
√
×
如图,学校要砌一个正方形花坛,已知外面的正方形边长为 cm,里面的正方形的边长为 cm,两个正方形的周长和为多少?
两个正方形的周长和为:
若两个正方形的面积分别为27cm2、12cm2,则两正方形的周长和为多少?
两个正方形的周长和为:
观察
以下是什么运算?如何计算?
二次根式的加法.
如何计算 呢?
分析: 类似8a+4a=12a,我们可以根据乘法分配律的逆用来进行运算。
探究
解:
如何计算 呢?
分析:题中二次根式不是最简二次根式,所以先要对其进行化简。再计算。
解:
讨论
仿照前两题,你能算出这个题吗?
有什么发现?
观察
计算:
有什么发现?
梳理
二次根式加减时,先将二次根式化为最简二次根式,再把被开方数相同的二次根式进行合并。
注意:对被开方数相同的二次根式进行合并,实质是对被开方数相同的二次根式的系数进行合并。
观察
化简:
每组二次根式在化简后有什么特点?
几个二次根式化为最简二次根式后,若被开方数相同,则这几个二次根式就叫做同类二次根式。
梳理
下列各组二次根式是否为同类二次根式?
探究
√
×
√
×
√
如何判断?
判断几个二次根式是否为同类二次根式的方法:
1、先化简:把各个二次根式都化为最简二次根式。
2、再观察:化简后的二次根式的被开方数是否相同。
梳理
例题讲解
1、计算:
解:
2、计算:
加减混合运算,应从左向右依次计算。
探究
解:原式=
别漏了“1”.
化简
解:原式=
下列解答是否正确?为什么?
错在没有按照二次根式加减混算从左向右依次进行的运算顺序计算。
运算不完全,能合并的没有合并。
P16练习1题
P17习题1题
归纳
二次根式的加减与整式的加减根据都是分配律,它们的运算实质也基本相同。
二次根式的加减即为对同类二次根式的合并。
先化为最简二次根式
把同类二次根式合并(合并系数)。
巩固练习
计算:
(3)合并同类二次根式。
一化
二找
三合并
二次根式加减法的步骤:
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
交流 归纳
