人教版数学八年级下册 19.2 一次函数复习课 PPT 课件(共38张PPT)
文档属性
| 名称 | 人教版数学八年级下册 19.2 一次函数复习课 PPT 课件(共38张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 08:12:33 | ||
图片预览










文档简介
(共38张PPT)
生活中充满着许许多多变化着的量与不变的量,它们之间还常常存在着一定的关系.函数是刻 画变量之间的关系的一个数学模型.
思一思
在一个过程中,可以取不同数值的量称为
变 量
在一个过程中,固定不变的量称为
常 量
小王家距离学校800米,小王每分钟步行100米,X分钟后小明距离学校Y米
这里的常量是______________________________________
这里的变量是____________________________
小王家离学校800米;小王步行速度100米/分钟
时间(X)和小王离学校的距离(Y)
1、一次函数y=_______(k、b为常数,k______)
当b_____时,函数y=kx叫做正比例函数。正比例函数是一次函数的特殊情况。
kx +b
=0
≠0
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
3、一次函数的性质
名 称 函数表达式
与图象 系数 符号 图象 性质
一次函数
正比例函数
一次函数
Y=kx(k≠0)图象是经过
(0,0),(1,k)两点的一条直线.
K>0
K<0
K>0
K<0
Y=kx+b(k≠0)图象是经过(0,b),
(-b/k,0)两点的一条直线.
b>0
b<0
b<0
b>0
Y随x增大而增大
Y随x增大而减少
Y随x增大而增大
Y随x增大而减少
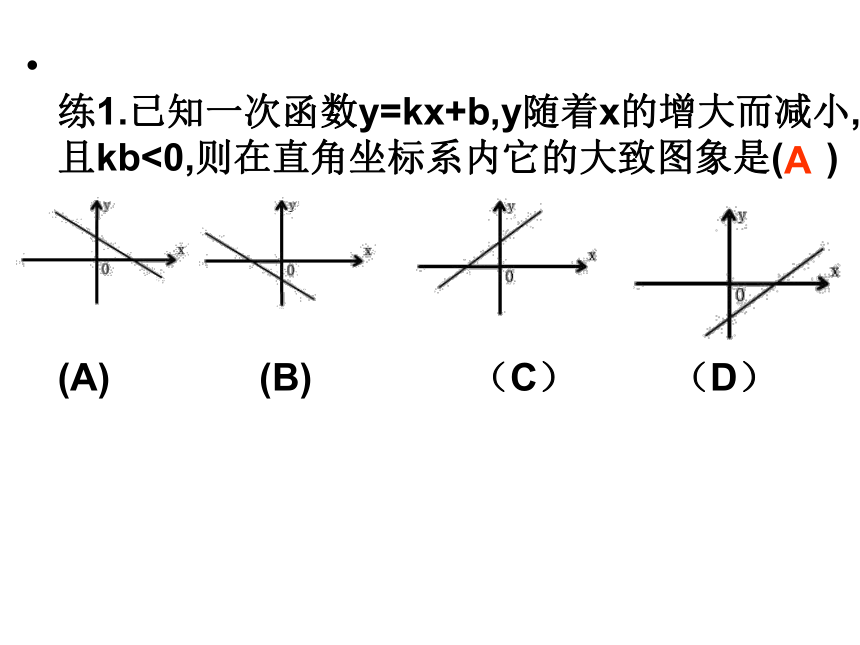
练1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)
A
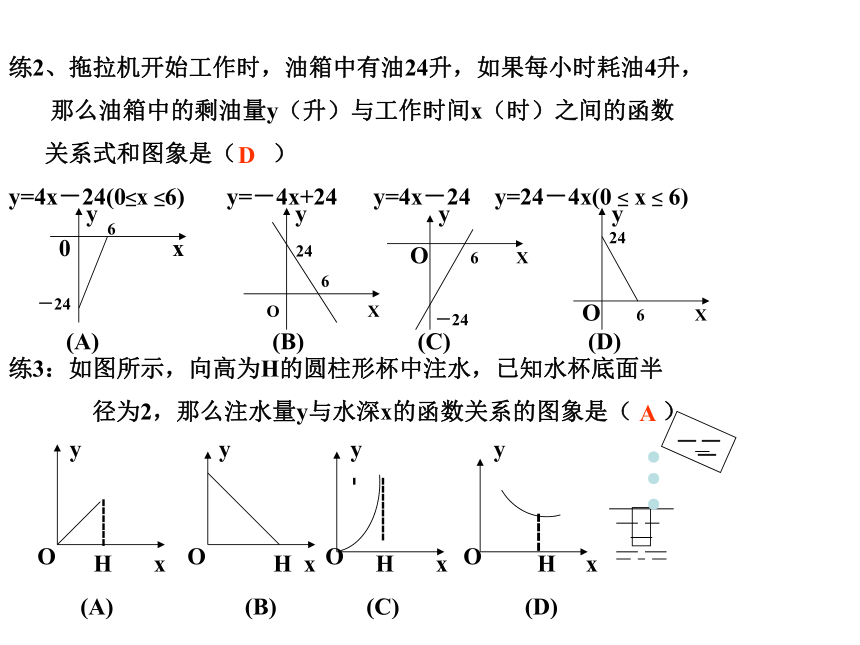
练2、拖拉机开始工作时,油箱中有油24升,如果每小时耗油4升,
那么油箱中的剩油量y(升)与工作时间x(时)之间的函数
关系式和图象是( )
y=4x-24(0≤x ≤6) y=-4x+24 y=4x-24 y=24-4x(0 ≤ x ≤ 6)
练3:如图所示,向高为H的圆柱形杯中注水,已知水杯底面半
径为2,那么注水量y与水深x的函数关系的图象是( )
y y y y
6
-24
0 x
24
6
O X
O 6 X
-24
24
O 6 X
D
(A) (B) (C) (D)
------
---------
----
y y y y
--
-
●
●
●
O O O O
H x H x H x H x
(A) (B) (C) (D)
A
例1已知一次函数
(1) k为何值时,它的图象经过原点
(2)k 为何值时,它的图象经过点(0, -2)
(3)k 为何值时,它的图象平行直线 y= - x
(4) k为何值时,它的图象向下平移后,
变成直线y=2x+8
(5)k 为何值时, y随x的增大而减 小
4、填空题:
(1) 有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。
②
①、②、③
④
③
(2)、已知y-1与x成正比例,且x=-2时,y=4,那么y与
x之间的函数关系式为_________________。
5、在下列函数中, x是自变量, y是x的函数, 那些是一次函数?那些是正比例函数?
y=2x y=-3x+1 y=x2
6、某函数具有下列两条性质
(1)它的图像是经过原点(0,0)的一条直线;
(2)y的值随x值的增大而增大。
请你举出一个满足上述条件的函数(用关系式表示)
7、函数 的图像与x轴交点坐标为________,
与y轴的交点坐标为____________。
8. 设点P(3,m),Q(n,2)都在函数y=x+b的图象上,
求m+n的值为————。
例2.求下列函数自变量的取值范围 (使函数式有意义):
练6 等腰三角形ABC周长为12cm,底边BC长为ycm,腰AB长为xcm.
(1)写出y关于x的函数关系式;
(2)求出x的取值范围;
(3)求出y的取值范围.
直线
与x轴交点
与y轴交点
y=2x+6
y=-x+6
y=-x
y=5x
(0,6)
(0,6)
( 6,0)
(-3,0)
在同一直角坐标系中作出下列函数的图象:
y= 2x+6
y= -x+6
y= -x,
y=5x
O
2
1
-1
-1
2
1
y=2x+6
-2
3
6
5
4
3
5
4
-3
-2
6
x
y
●
●
●
一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。
(0,b)
x
y
o
y=2x+1
x
y
o
y=2x
x
y
o
y=2x
y=2x-1
直线y=2x-1是由直线y=2x向下平移 个单位得到。
1
直线y=2x-3是由直线y=2x+1向 平移 个单位得到。
下
4
② 因为函数图象过点(3,5)和(- 4,-9),则
5=3k+b
-9=-4k+b
k=2
b=-1
例3:已知函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式。
所以函数的解析式为:y=2x-1.
解: ①设这个函数的解析式为
(1)先设出函数解析式
用待定系数法求函数解析式步骤:
(2)根据条件建立含k,b的两个方程
(3)解方程组求出待定字母
9、 对于函数 , y的值随x值的____而增大。
10、直线y=kx+b过点(1,3)和点(-1,1),则
=__________。
11、已知一次函数 y=(6+3m)x+n-4,n为何值时,函数图象与y轴交点在x轴的下方?
数形结合训练:
1、已知一次函数y=kx+b(k≠0)平行于
直线y=3x,且过点(1,4),求函数解析式。
2、已知一次函数y=kx+b(k≠0)在y轴上
的截距是-2,且过点(1,3),求函数解析式。
函数解析式为:y=3x+1
函数解析式为:y=5x-2
3、在直角坐标系中,一次函数y=kx+b的图像经过三
点A(2,0)、B(0,2)、C(m,3),求这个函数
的关系式,并求m的值。
4、已知一次函数的图像经过点A(2,-1)和点B,
其中点B是另一条直线 与y轴的交点,求这
个一次函数的表达式。
解:由一次函数当x=1时,y=5;且它的图象与x轴交点
是(6,0),得
解得
∴一次函数的解析式为 y= - x+6。
点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。
5、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。
例4、已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=-3时y的值和y =-3时x的值。
解:由 y与x-1成正比例可设y=k(x-1)
∵ 当x=8时,y=6 ∴7k=6 ∴
∴ y与x之间函数关系式是:y= (x-1)
当x=4时,y= ×(4-1)=
当y =-3时,-3= (X-1) X=
有两条直线l1:y=ax+b 和l2:y=cx-5,学生甲解出它们的交点为(3,-2);乙学生因看错c而解出它们 的交点为(3/4,1/4),试写出这两条直线的表达式与x轴所围成的三角形面积.
例5、 柴油机在工作时油箱中的余油量Q(千克)
与工作时间t(小时)成一次函数关系,当工作开始时
油箱中有油40千克,工作3.5小时后,油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式;(2)画出
这个函数的图象。
解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5,分别代入上式,得
解得
解析式为:Q=-5t+40 (0≤t≤8)
(2)、取t=0,得Q=40;取t=8,得Q=0。描出点
A(0,40),B(8,0)。然后连成线段AB即是所
求的图形。
注意:
(1)求出函数关系式时,必须找出自变量的取值范围。
(2)画函数图象时,应根据函数自变量的取值范围来确定图象的范围。
20
40
8
0
t
Q
图象是包括
两端点的线段
.
.
A
B
练1.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的
距离为 千米.
2、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。
(2)服药5时,血液中含药量为每毫升____毫克。
(3)当x≤2时y与x之间的函数关系式是_____。
(4)当x≥2时y与x之间的函数关系式是____。
(5)如果每毫升血液中含药量3毫克或3毫克以上
时,治疗疾病最有效,那么这个有效时间范围是___时。.
x/时
y/毫克
6
3
2
5
O
生活中有许许多多的问题是可以用一次函数去解决的,但此时又往往会出现两个函数关系,让你择优的选取一个,你会怎样选取呢?
为了适应新课程教学,我校需配置一批电脑。现在有甲、乙两家公司与 我校联系,已知甲公司的报价为每台5800元,优惠条件是购买10台以上则从第11台开始可以按报价的70%计算;乙公司的报价也是5800元,但优惠条件是每台均按报价的85%计算。在电脑品牌、质量等完全相同的前提下,如果让你去购买,你该如何选择?
(1)购买不多于10台电脑时,应该选甲还是乙?
讨论:
如何选择?
甲报价为5800元,购买10台以上则从第11台开始按报价的70%计算;乙报价也是5800元,但每台均按报价的85%计算。若购买的台数没有限制,如何选择?请说明理由。
甲公司
乙公司
Y甲=5800×10+ 5800(x-10)·70%
Y乙=5800x · 85%
若Y甲 = Y乙
∴x=20
∴x>20
选甲公司或乙公司
选乙公司
∴10若Y甲 < Y乙
选甲公司
若学校购买的电脑台数少于20台,则选乙公司合算
若学校购买的电脑台数等于20台,则选甲或乙公司都一样;
若学校购买的电脑台数多于20台,则选甲公司合算;
若Y甲 >Y乙
X取整数
(1)某地市话费收费标准为:通话时间在三分钟以内(包括三分钟),话费为每分钟0.6元;通话时间超过了三分钟,超过部分按每分钟0.2元。则总话费(元)与通话时间x(取整数)之间的关系式为 :
(2)某风景区集体门票的收费标准为:20人以内(含20人),每人25元;超过20人,超过部分每人10元,则应收门票y元与游览人数x人之间的关系式为:______________;
840
某班54名学生去该风景区游览,购买门票共花去______元。
某家电信公司提供了两种方案的移动通讯服务的收费标准,如下表:
A方案 B方案
每月基本服务费 30元 50元
每月免费通话时间 120分 200分
超出后每分收费 0.4元 0.4元
1、在服务质量相同的情况下,人们通常根据什么来选取择方案?
2、每种方案每月付金费额与什么相关?
3、怎样表示每月话费与通话时间的关系?
请从以下几方面考虑:
250
(元)
X(分)
y
150
100
50
100
50
200
170
150
300
0
A方案
B方案
在同一直角坐标系中画出图象,如图:
观察图象得到:
为了缓解用电紧张的矛盾,电力公司制定了新的用电收费标准,每月用电量x(千瓦时)与应付电费y(元)的关系如图所示:
25
50
75
100
25
50
75
100
70
X(千瓦时)
Y(元)
0
(1)根据图象求出y与x的函数关系式;
(2)请回答电力公司的收费标准是什么?
这节课你有何收获,
能与大家分享、交流你的感受吗?
布置作业:
见数学一课一练中的单元评估题
生活中充满着许许多多变化着的量与不变的量,它们之间还常常存在着一定的关系.函数是刻 画变量之间的关系的一个数学模型.
思一思
在一个过程中,可以取不同数值的量称为
变 量
在一个过程中,固定不变的量称为
常 量
小王家距离学校800米,小王每分钟步行100米,X分钟后小明距离学校Y米
这里的常量是______________________________________
这里的变量是____________________________
小王家离学校800米;小王步行速度100米/分钟
时间(X)和小王离学校的距离(Y)
1、一次函数y=_______(k、b为常数,k______)
当b_____时,函数y=kx叫做正比例函数。正比例函数是一次函数的特殊情况。
kx +b
=0
≠0
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
3、一次函数的性质
名 称 函数表达式
与图象 系数 符号 图象 性质
一次函数
正比例函数
一次函数
Y=kx(k≠0)图象是经过
(0,0),(1,k)两点的一条直线.
K>0
K<0
K>0
K<0
Y=kx+b(k≠0)图象是经过(0,b),
(-b/k,0)两点的一条直线.
b>0
b<0
b<0
b>0
Y随x增大而增大
Y随x增大而减少
Y随x增大而增大
Y随x增大而减少
练1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)
A
练2、拖拉机开始工作时,油箱中有油24升,如果每小时耗油4升,
那么油箱中的剩油量y(升)与工作时间x(时)之间的函数
关系式和图象是( )
y=4x-24(0≤x ≤6) y=-4x+24 y=4x-24 y=24-4x(0 ≤ x ≤ 6)
练3:如图所示,向高为H的圆柱形杯中注水,已知水杯底面半
径为2,那么注水量y与水深x的函数关系的图象是( )
y y y y
6
-24
0 x
24
6
O X
O 6 X
-24
24
O 6 X
D
(A) (B) (C) (D)
------
---------
----
y y y y
--
-
●
●
●
O O O O
H x H x H x H x
(A) (B) (C) (D)
A
例1已知一次函数
(1) k为何值时,它的图象经过原点
(2)k 为何值时,它的图象经过点(0, -2)
(3)k 为何值时,它的图象平行直线 y= - x
(4) k为何值时,它的图象向下平移后,
变成直线y=2x+8
(5)k 为何值时, y随x的增大而减 小
4、填空题:
(1) 有下列函数:① , ② ,
③ , ④ 。其中过原点的直
线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____。
②
①、②、③
④
③
(2)、已知y-1与x成正比例,且x=-2时,y=4,那么y与
x之间的函数关系式为_________________。
5、在下列函数中, x是自变量, y是x的函数, 那些是一次函数?那些是正比例函数?
y=2x y=-3x+1 y=x2
6、某函数具有下列两条性质
(1)它的图像是经过原点(0,0)的一条直线;
(2)y的值随x值的增大而增大。
请你举出一个满足上述条件的函数(用关系式表示)
7、函数 的图像与x轴交点坐标为________,
与y轴的交点坐标为____________。
8. 设点P(3,m),Q(n,2)都在函数y=x+b的图象上,
求m+n的值为————。
例2.求下列函数自变量的取值范围 (使函数式有意义):
练6 等腰三角形ABC周长为12cm,底边BC长为ycm,腰AB长为xcm.
(1)写出y关于x的函数关系式;
(2)求出x的取值范围;
(3)求出y的取值范围.
直线
与x轴交点
与y轴交点
y=2x+6
y=-x+6
y=-x
y=5x
(0,6)
(0,6)
( 6,0)
(-3,0)
在同一直角坐标系中作出下列函数的图象:
y= 2x+6
y= -x+6
y= -x,
y=5x
O
2
1
-1
-1
2
1
y=2x+6
-2
3
6
5
4
3
5
4
-3
-2
6
x
y
●
●
●
一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。
(0,b)
x
y
o
y=2x+1
x
y
o
y=2x
x
y
o
y=2x
y=2x-1
直线y=2x-1是由直线y=2x向下平移 个单位得到。
1
直线y=2x-3是由直线y=2x+1向 平移 个单位得到。
下
4
② 因为函数图象过点(3,5)和(- 4,-9),则
5=3k+b
-9=-4k+b
k=2
b=-1
例3:已知函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式。
所以函数的解析式为:y=2x-1.
解: ①设这个函数的解析式为
(1)先设出函数解析式
用待定系数法求函数解析式步骤:
(2)根据条件建立含k,b的两个方程
(3)解方程组求出待定字母
9、 对于函数 , y的值随x值的____而增大。
10、直线y=kx+b过点(1,3)和点(-1,1),则
=__________。
11、已知一次函数 y=(6+3m)x+n-4,n为何值时,函数图象与y轴交点在x轴的下方?
数形结合训练:
1、已知一次函数y=kx+b(k≠0)平行于
直线y=3x,且过点(1,4),求函数解析式。
2、已知一次函数y=kx+b(k≠0)在y轴上
的截距是-2,且过点(1,3),求函数解析式。
函数解析式为:y=3x+1
函数解析式为:y=5x-2
3、在直角坐标系中,一次函数y=kx+b的图像经过三
点A(2,0)、B(0,2)、C(m,3),求这个函数
的关系式,并求m的值。
4、已知一次函数的图像经过点A(2,-1)和点B,
其中点B是另一条直线 与y轴的交点,求这
个一次函数的表达式。
解:由一次函数当x=1时,y=5;且它的图象与x轴交点
是(6,0),得
解得
∴一次函数的解析式为 y= - x+6。
点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。
5、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。
例4、已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=-3时y的值和y =-3时x的值。
解:由 y与x-1成正比例可设y=k(x-1)
∵ 当x=8时,y=6 ∴7k=6 ∴
∴ y与x之间函数关系式是:y= (x-1)
当x=4时,y= ×(4-1)=
当y =-3时,-3= (X-1) X=
有两条直线l1:y=ax+b 和l2:y=cx-5,学生甲解出它们的交点为(3,-2);乙学生因看错c而解出它们 的交点为(3/4,1/4),试写出这两条直线的表达式与x轴所围成的三角形面积.
例5、 柴油机在工作时油箱中的余油量Q(千克)
与工作时间t(小时)成一次函数关系,当工作开始时
油箱中有油40千克,工作3.5小时后,油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式;(2)画出
这个函数的图象。
解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5,分别代入上式,得
解得
解析式为:Q=-5t+40 (0≤t≤8)
(2)、取t=0,得Q=40;取t=8,得Q=0。描出点
A(0,40),B(8,0)。然后连成线段AB即是所
求的图形。
注意:
(1)求出函数关系式时,必须找出自变量的取值范围。
(2)画函数图象时,应根据函数自变量的取值范围来确定图象的范围。
20
40
8
0
t
Q
图象是包括
两端点的线段
.
.
A
B
练1.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的
距离为 千米.
2、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。
(2)服药5时,血液中含药量为每毫升____毫克。
(3)当x≤2时y与x之间的函数关系式是_____。
(4)当x≥2时y与x之间的函数关系式是____。
(5)如果每毫升血液中含药量3毫克或3毫克以上
时,治疗疾病最有效,那么这个有效时间范围是___时。.
x/时
y/毫克
6
3
2
5
O
生活中有许许多多的问题是可以用一次函数去解决的,但此时又往往会出现两个函数关系,让你择优的选取一个,你会怎样选取呢?
为了适应新课程教学,我校需配置一批电脑。现在有甲、乙两家公司与 我校联系,已知甲公司的报价为每台5800元,优惠条件是购买10台以上则从第11台开始可以按报价的70%计算;乙公司的报价也是5800元,但优惠条件是每台均按报价的85%计算。在电脑品牌、质量等完全相同的前提下,如果让你去购买,你该如何选择?
(1)购买不多于10台电脑时,应该选甲还是乙?
讨论:
如何选择?
甲报价为5800元,购买10台以上则从第11台开始按报价的70%计算;乙报价也是5800元,但每台均按报价的85%计算。若购买的台数没有限制,如何选择?请说明理由。
甲公司
乙公司
Y甲=5800×10+ 5800(x-10)·70%
Y乙=5800x · 85%
若Y甲 = Y乙
∴x=20
∴x>20
选甲公司或乙公司
选乙公司
∴10
选甲公司
若学校购买的电脑台数少于20台,则选乙公司合算
若学校购买的电脑台数等于20台,则选甲或乙公司都一样;
若学校购买的电脑台数多于20台,则选甲公司合算;
若Y甲 >Y乙
X取整数
(1)某地市话费收费标准为:通话时间在三分钟以内(包括三分钟),话费为每分钟0.6元;通话时间超过了三分钟,超过部分按每分钟0.2元。则总话费(元)与通话时间x(取整数)之间的关系式为 :
(2)某风景区集体门票的收费标准为:20人以内(含20人),每人25元;超过20人,超过部分每人10元,则应收门票y元与游览人数x人之间的关系式为:______________;
840
某班54名学生去该风景区游览,购买门票共花去______元。
某家电信公司提供了两种方案的移动通讯服务的收费标准,如下表:
A方案 B方案
每月基本服务费 30元 50元
每月免费通话时间 120分 200分
超出后每分收费 0.4元 0.4元
1、在服务质量相同的情况下,人们通常根据什么来选取择方案?
2、每种方案每月付金费额与什么相关?
3、怎样表示每月话费与通话时间的关系?
请从以下几方面考虑:
250
(元)
X(分)
y
150
100
50
100
50
200
170
150
300
0
A方案
B方案
在同一直角坐标系中画出图象,如图:
观察图象得到:
为了缓解用电紧张的矛盾,电力公司制定了新的用电收费标准,每月用电量x(千瓦时)与应付电费y(元)的关系如图所示:
25
50
75
100
25
50
75
100
70
X(千瓦时)
Y(元)
0
(1)根据图象求出y与x的函数关系式;
(2)请回答电力公司的收费标准是什么?
这节课你有何收获,
能与大家分享、交流你的感受吗?
布置作业:
见数学一课一练中的单元评估题
