人教版数学八年级下册 17.2 勾股定理的逆定理3 教案
文档属性
| 名称 | 人教版数学八年级下册 17.2 勾股定理的逆定理3 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 311.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 08:35:25 | ||
图片预览

文档简介
17.2勾股定理的逆定理
一、教学目标
知识目标:
1、体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2、探究勾股定理的逆定理的证明方法。
3、理解原命题、逆命题、逆定理的概念及关系。
能力目标:(1)通过对勾股定理的逆定理的探索,经历知识的发生、发展和形成的过程;
(2)通过用三角形的三边的数量关系来判断三角形的形状,体验数形结合方法的应用。
情感目标:(1)通过用三角形的三边的数量关系来判断三角形的形状,体验数与形的内在联系,感受定理与逆定理之间的和谐及辩证统一的关系;
(2)通过对勾股定理的逆定理的探索,培养了学生的交流、合作的意识和严谨的学习态度。同时感悟勾股定理和逆定理的应用价值。
二、教学重点难点
重点:证明勾股定理的逆定理;用勾股定理的逆定理解决具体的问题。
难点:理解勾股定理的逆定理的推导。
三、教学准备
圆规、三角板、一根打了13个等距离结的细绳子、钉子、小黑板
四、教学过程
(1)复习旧课
1、什么是勾股定理?
2、勾股定理的变试。
(2)情境导入
1、在古代,没有直尺、圆规等作图工具,人们是怎样画直角三角形的呢?
【实验观察】
用一根打了13个等距离结的细绳子,在小黑板上,用钉子钉在第一个结上,再钉在第4个结上,再钉在第8个结上,最后将第十三个结与第一个结钉在一起.然后用三角板量出最大角的度数.可以发现这个三角形是直角三角形。(这是古埃及人画直角的方法)
2、 用圆规、刻度尺作△ABC,使AB=5㎝,AC=4㎝,BC=3㎝,量一量∠C。
再画一个三角形,使它的三边长分别是5㎝、12㎝、13㎝,这个三角形有什么特征?
3、为什么用上面的三条线段围成的三角形,就一定是直角三角形呢?它们的三边有怎样的关系?(学生分组讨论,教师适当指导)
学生猜想:如果一个三角形的三边长满足下面的关系,那么这个三角形是直角三角形。
4、指出这个命题的题设和结论,对比勾股定理,理解互逆命题。
(3)探究新知
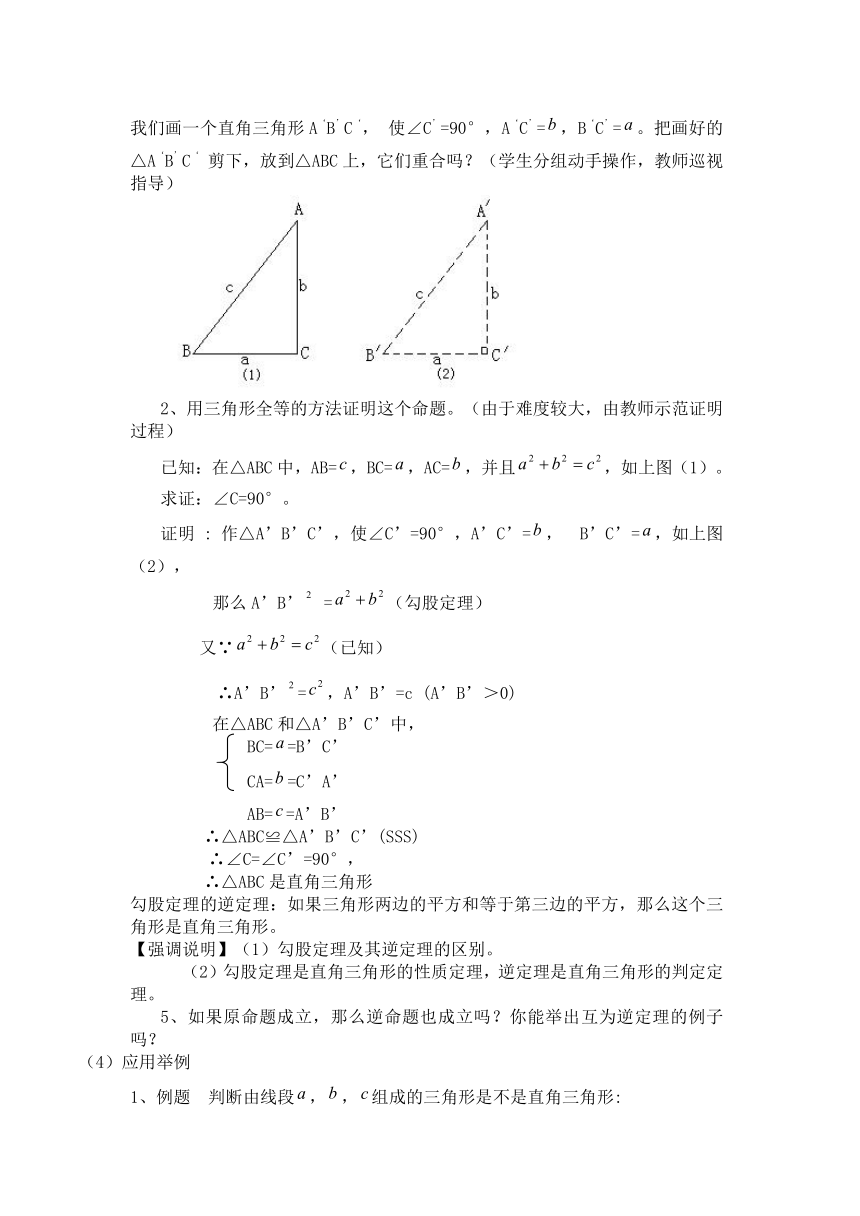
1、探究:在下图中,△ABC的三边长,,满足。如果△ABC是直角三角形,它应该与直角边是,的直角三角形全等。实际情况是这样吗?我们画一个直角三角形A‘B’C‘, 使∠C’=90°,A‘C’=,B‘C’=。把画好的△A‘B’C‘ 剪下,放到△ABC上,它们重合吗?(学生分组动手操作,教师巡视指导)
2、用三角形全等的方法证明这个命题。(由于难度较大,由教师示范证明过程)
已知:在△ABC中,AB=,BC=,AC=,并且,如上图(1)。
求证:∠C=90°。
证明 : 作△A’B’C’,使∠C’=90°,A’C’=, B’C’=,如上图(2),
那么A’B’ =(勾股定理)
又∵(已知)
∴A’B’=,A’B’=c (A’B’>0)
在△ABC和△A’B’C’中,
BC==B’C’
CA==C’A’
AB==A’B’
∴△ABC≌△A’B’C’(SSS)
∴∠C=∠C’=90°,
∴△ABC是直角三角形
勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
【强调说明】(1)勾股定理及其逆定理的区别。
(2)勾股定理是直角三角形的性质定理,逆定理是直角三角形的判定定理。
5、如果原命题成立,那么逆命题也成立吗?你能举出互为逆定理的例子吗?
(4)应用举例
1、例题 判断由线段,,组成的三角形是不是直角三角形:
(1),,;
(2),,。
2、像15、8、17这样,能够成为直角三角形三条边长度的三个正整数,称为勾股数。你还能举出其它一组勾股数吗?
(5)练习巩固
1. 判断由线段,,组成的三角形是不是直角三角形:
(1),,;
(2),,;
(3),,;
(4),,。
2.如果三条线段长,,满足,这三条线段组成的三角形是不是直角三角形 为什么
3.说出下列命题的逆命题。这些命题的逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)角的内部到角的两边的距离相等的点在角的平分线上。
(6)、课堂总结
通过这节课的学习,你有什么收获?还有什么困惑?
这节课我们学习了:
1、勾股定理的逆定理。
2、如何证明勾股定理的逆定理。
3、互逆命题和互逆定理。
4、利用勾股定理的逆定理判定一个三角形是否为直角三角形。
(7)作业布置
P76习题18.2第2、4题。
板书设计
17.2勾股定理的逆定理
古埃及人画直角的方法二、猜想:如果一个三角形的三边长满足下面的关系,那么这个三角形是直角三角形。 三、探究勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。四、应用举例五、练习巩固 六、课堂总结七、作业布置
PAGE
一、教学目标
知识目标:
1、体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2、探究勾股定理的逆定理的证明方法。
3、理解原命题、逆命题、逆定理的概念及关系。
能力目标:(1)通过对勾股定理的逆定理的探索,经历知识的发生、发展和形成的过程;
(2)通过用三角形的三边的数量关系来判断三角形的形状,体验数形结合方法的应用。
情感目标:(1)通过用三角形的三边的数量关系来判断三角形的形状,体验数与形的内在联系,感受定理与逆定理之间的和谐及辩证统一的关系;
(2)通过对勾股定理的逆定理的探索,培养了学生的交流、合作的意识和严谨的学习态度。同时感悟勾股定理和逆定理的应用价值。
二、教学重点难点
重点:证明勾股定理的逆定理;用勾股定理的逆定理解决具体的问题。
难点:理解勾股定理的逆定理的推导。
三、教学准备
圆规、三角板、一根打了13个等距离结的细绳子、钉子、小黑板
四、教学过程
(1)复习旧课
1、什么是勾股定理?
2、勾股定理的变试。
(2)情境导入
1、在古代,没有直尺、圆规等作图工具,人们是怎样画直角三角形的呢?
【实验观察】
用一根打了13个等距离结的细绳子,在小黑板上,用钉子钉在第一个结上,再钉在第4个结上,再钉在第8个结上,最后将第十三个结与第一个结钉在一起.然后用三角板量出最大角的度数.可以发现这个三角形是直角三角形。(这是古埃及人画直角的方法)
2、 用圆规、刻度尺作△ABC,使AB=5㎝,AC=4㎝,BC=3㎝,量一量∠C。
再画一个三角形,使它的三边长分别是5㎝、12㎝、13㎝,这个三角形有什么特征?
3、为什么用上面的三条线段围成的三角形,就一定是直角三角形呢?它们的三边有怎样的关系?(学生分组讨论,教师适当指导)
学生猜想:如果一个三角形的三边长满足下面的关系,那么这个三角形是直角三角形。
4、指出这个命题的题设和结论,对比勾股定理,理解互逆命题。
(3)探究新知
1、探究:在下图中,△ABC的三边长,,满足。如果△ABC是直角三角形,它应该与直角边是,的直角三角形全等。实际情况是这样吗?我们画一个直角三角形A‘B’C‘, 使∠C’=90°,A‘C’=,B‘C’=。把画好的△A‘B’C‘ 剪下,放到△ABC上,它们重合吗?(学生分组动手操作,教师巡视指导)
2、用三角形全等的方法证明这个命题。(由于难度较大,由教师示范证明过程)
已知:在△ABC中,AB=,BC=,AC=,并且,如上图(1)。
求证:∠C=90°。
证明 : 作△A’B’C’,使∠C’=90°,A’C’=, B’C’=,如上图(2),
那么A’B’ =(勾股定理)
又∵(已知)
∴A’B’=,A’B’=c (A’B’>0)
在△ABC和△A’B’C’中,
BC==B’C’
CA==C’A’
AB==A’B’
∴△ABC≌△A’B’C’(SSS)
∴∠C=∠C’=90°,
∴△ABC是直角三角形
勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
【强调说明】(1)勾股定理及其逆定理的区别。
(2)勾股定理是直角三角形的性质定理,逆定理是直角三角形的判定定理。
5、如果原命题成立,那么逆命题也成立吗?你能举出互为逆定理的例子吗?
(4)应用举例
1、例题 判断由线段,,组成的三角形是不是直角三角形:
(1),,;
(2),,。
2、像15、8、17这样,能够成为直角三角形三条边长度的三个正整数,称为勾股数。你还能举出其它一组勾股数吗?
(5)练习巩固
1. 判断由线段,,组成的三角形是不是直角三角形:
(1),,;
(2),,;
(3),,;
(4),,。
2.如果三条线段长,,满足,这三条线段组成的三角形是不是直角三角形 为什么
3.说出下列命题的逆命题。这些命题的逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)角的内部到角的两边的距离相等的点在角的平分线上。
(6)、课堂总结
通过这节课的学习,你有什么收获?还有什么困惑?
这节课我们学习了:
1、勾股定理的逆定理。
2、如何证明勾股定理的逆定理。
3、互逆命题和互逆定理。
4、利用勾股定理的逆定理判定一个三角形是否为直角三角形。
(7)作业布置
P76习题18.2第2、4题。
板书设计
17.2勾股定理的逆定理
古埃及人画直角的方法二、猜想:如果一个三角形的三边长满足下面的关系,那么这个三角形是直角三角形。 三、探究勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。四、应用举例五、练习巩固 六、课堂总结七、作业布置
PAGE
