2021-2022学年 人教版 七年级数学上册 4.3.2角的比较与运算 课件(26张PPT)
文档属性
| 名称 | 2021-2022学年 人教版 七年级数学上册 4.3.2角的比较与运算 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 456.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
角的比较与运算(第一课时)
人教版 七年级数学上册
主讲人:
1. 理解角的大小、和差、角平分线的几何意义及数量关系,并能解答相关问题。
2. 经过类比线段的长短、和差、中点学习角的大小、和差、角平分线,体会类比的思想。
学习目标
有一天学生张亮和王帅各带了一把折扇(如图所示),
下面是他们的一段对话:
张:我的折扇张开大一些,所以我的折扇的角也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
同学们,你们有办法帮他们进行判断吗
情境导入
线段长短的比较
温故知新
AB>CD
ABAB=CD
A
B
C
D
A
B
A
B
C
D
C
D
类比线段大小的比较,你认为该如何比较两个角的大小?试着画图来解决.
1. 度量法
一、角的比较与运算
类比探究
步骤:
1. 将两个角的顶点及一边重合,
2. 两个角的另一边落在重合一边的同侧,
3.由两个角的另一边的位置确定两个角的大小.
类比探究
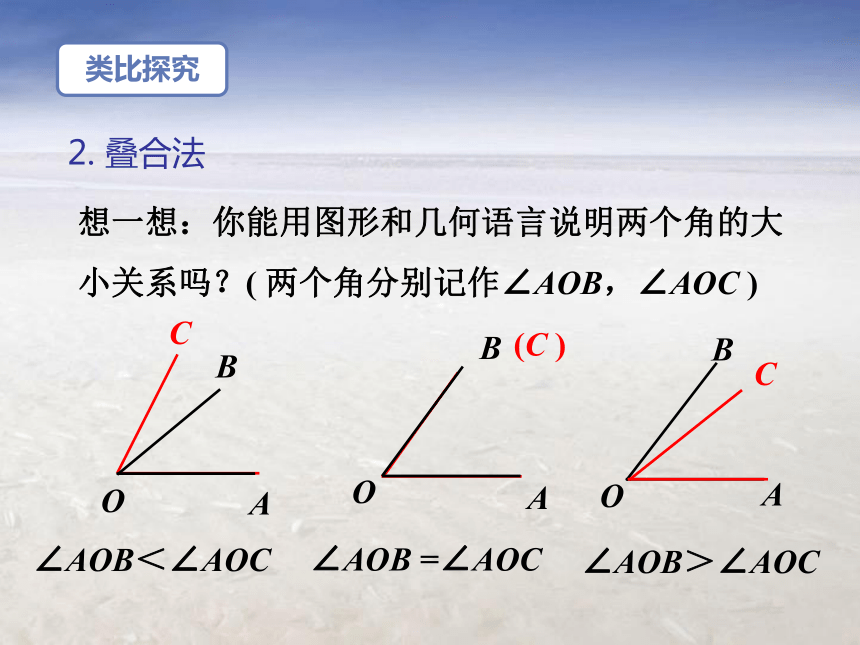
2. 叠合法
∠AOB<∠AOC
∠AOB =∠AOC
∠AOB>∠AOC
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠AOC )
类比探究
2. 叠合法
A
B
O
C
(C )
C
O
A
B
A
B
O
如图,把∠A的两边延长,∠A的大小改变了吗?角的大小与什么有关?
A
解:∠A大小没变。角的大小与角的两边画出的长短没有关系。角的大小与两条边开口大小有关,开口越大,角越大 。
思考
AB = BC+AC
BC = AB-AC
AC = AB-BC
线段的和、差
温故知新
问题1:图中共有几个角?它们之间有什么数量关系?
答:有三个角,关系是:
∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC;
∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC;
∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.
A
B
O
C
类比探究
二、角的和差
A
B
O
C
问题2: 当射线OB 在 ∠AOC 内部和外部时他们之间的数量关系有变化吗
类比探究
A
B
O
C
A
B
O
C
这三个角的关系又是什么?
这三个角的关系是什么?
∠AOC=∠AOB+∠BOC,
∠AOB=∠AOC-∠BOC,
∠BOC=∠AOC-∠AOB.
∠AOC=∠BOC-∠BOA,
∠AOB=∠BOC-∠AOC,
∠BOC=∠COA+∠AOB.
问题2: 当射线OB 在 ∠AOC 内部和外部时他们之间的数量关系有变化吗
类比探究
线段中点
若点C位于线段AB的中点,则
AC = BC
AC = BC = AB
AB = 2 AC = 2 BC
温故知新
我们把射线OB叫做∠AOC的角平分线.
射线OB在∠AOC的内部有没有一种特殊的位置?
我们来看图猜测此时三个角之间有怎样的关系?
A
B
O
C
∠AOB_____∠BOC;
=
∠AOC=_____∠AOB=_____∠BOC
2
2
类比探究
三、角的平分线
类比线段中点的定义,你能给角平分线下定义吗?
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
∵ OB是∠AOC 的角平分线,
∴ ∠AOB=∠BOC = ∠AOC,
∠AOC=2∠AOB=2∠BOC.
A
B
O
C
类比探究
类似地,还有角的三等分线、四等分线。
α
α
α
α
α
α
α
类比探究
利用一副三角板,你能画出哪些度数的角?试一试。
合作探究
75°
15 °
120 °
15 ° , 30° , 45 ° , 60° , 75 °, 90°,
105 °,120 °,135 °,150 °,165°,180 °
动手做一做:在纸上画∠AOB,然后将其剪下来,如何通过折纸把角平分?
将其沿经过顶点的线对折,使边OA与OB重合。
将角展开,折痕上任取一点记作点C,射线OC是角平分线。
合作探究
例1. 如图,填空:
(1)∠DAB = ∠DAC+ .
(2)∠ACB = ∠DCB – .
∠CAB
∠DCA
A
B
D
C
典例分析
例2:如图,OB 是∠AOC 的平分线.
(1) 如果∠AOC=80°,那么∠AOB 是多少度?
O
A
B
C
D
解:因为 :OB 平分∠AOC,
∠AOC=80°,
所以:
∠AOB= ∠AOC= ×80°=40°
(2) 如果∠AOD=100°,∠COD=20°,那么∠BOD是多少度?
O
A
B
C
D
所以∠BOD= ∠BOC+∠COD= 40°+ 20°= 60°
解:因为 ∠COD = 20°,
所以 ∠AOC= ∠AOD-∠COD
= 100°-20°= 80°
又因为 OB 平分∠AOC,
所以∠AOB= ∠AOC = ×80°= 40°
1.如图,AM为∠BAC的平分线,下列等式错误的是( )
A.∠BAM = ∠BAC
B.∠BAM = ∠CAM
C.∠BAM = 2∠CAM
D.2∠CAM = ∠BAC
C
2、若∠AOB=60°, ∠BOC=40°, 求∠AOC.
A
C
B
O
A
C
B
O
当堂巩固
课堂小结
线
段
的
运
算
与
比
较
线段的比较
线段的运算
角 的 比 较
角的运算
度 量 法
叠 合 法
线段和差
线段的计算
线段中点
角的
运
算
与
比
较
角的和差
角平分线
角的计算
课堂小结
D
C
A
B
2.如图∠AOE=120°,OC是∠AOE内部任意一条射线,OB,OE分别为∠AOC,∠COE的角平分线,求∠BOD
A
B
C
D
E
拓展延伸
1.如图,线段AE=10,C为线段AE上任意一点,D,B分别为AC,CE中点,求BD的长
O
A
B
C
D
E
谢谢!
角的比较与运算(第一课时)
人教版 七年级数学上册
主讲人:
1. 理解角的大小、和差、角平分线的几何意义及数量关系,并能解答相关问题。
2. 经过类比线段的长短、和差、中点学习角的大小、和差、角平分线,体会类比的思想。
学习目标
有一天学生张亮和王帅各带了一把折扇(如图所示),
下面是他们的一段对话:
张:我的折扇张开大一些,所以我的折扇的角也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
同学们,你们有办法帮他们进行判断吗
情境导入
线段长短的比较
温故知新
AB>CD
AB
A
B
C
D
A
B
A
B
C
D
C
D
类比线段大小的比较,你认为该如何比较两个角的大小?试着画图来解决.
1. 度量法
一、角的比较与运算
类比探究
步骤:
1. 将两个角的顶点及一边重合,
2. 两个角的另一边落在重合一边的同侧,
3.由两个角的另一边的位置确定两个角的大小.
类比探究
2. 叠合法
∠AOB<∠AOC
∠AOB =∠AOC
∠AOB>∠AOC
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠AOC )
类比探究
2. 叠合法
A
B
O
C
(C )
C
O
A
B
A
B
O
如图,把∠A的两边延长,∠A的大小改变了吗?角的大小与什么有关?
A
解:∠A大小没变。角的大小与角的两边画出的长短没有关系。角的大小与两条边开口大小有关,开口越大,角越大 。
思考
AB = BC+AC
BC = AB-AC
AC = AB-BC
线段的和、差
温故知新
问题1:图中共有几个角?它们之间有什么数量关系?
答:有三个角,关系是:
∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC;
∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC;
∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.
A
B
O
C
类比探究
二、角的和差
A
B
O
C
问题2: 当射线OB 在 ∠AOC 内部和外部时他们之间的数量关系有变化吗
类比探究
A
B
O
C
A
B
O
C
这三个角的关系又是什么?
这三个角的关系是什么?
∠AOC=∠AOB+∠BOC,
∠AOB=∠AOC-∠BOC,
∠BOC=∠AOC-∠AOB.
∠AOC=∠BOC-∠BOA,
∠AOB=∠BOC-∠AOC,
∠BOC=∠COA+∠AOB.
问题2: 当射线OB 在 ∠AOC 内部和外部时他们之间的数量关系有变化吗
类比探究
线段中点
若点C位于线段AB的中点,则
AC = BC
AC = BC = AB
AB = 2 AC = 2 BC
温故知新
我们把射线OB叫做∠AOC的角平分线.
射线OB在∠AOC的内部有没有一种特殊的位置?
我们来看图猜测此时三个角之间有怎样的关系?
A
B
O
C
∠AOB_____∠BOC;
=
∠AOC=_____∠AOB=_____∠BOC
2
2
类比探究
三、角的平分线
类比线段中点的定义,你能给角平分线下定义吗?
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
∵ OB是∠AOC 的角平分线,
∴ ∠AOB=∠BOC = ∠AOC,
∠AOC=2∠AOB=2∠BOC.
A
B
O
C
类比探究
类似地,还有角的三等分线、四等分线。
α
α
α
α
α
α
α
类比探究
利用一副三角板,你能画出哪些度数的角?试一试。
合作探究
75°
15 °
120 °
15 ° , 30° , 45 ° , 60° , 75 °, 90°,
105 °,120 °,135 °,150 °,165°,180 °
动手做一做:在纸上画∠AOB,然后将其剪下来,如何通过折纸把角平分?
将其沿经过顶点的线对折,使边OA与OB重合。
将角展开,折痕上任取一点记作点C,射线OC是角平分线。
合作探究
例1. 如图,填空:
(1)∠DAB = ∠DAC+ .
(2)∠ACB = ∠DCB – .
∠CAB
∠DCA
A
B
D
C
典例分析
例2:如图,OB 是∠AOC 的平分线.
(1) 如果∠AOC=80°,那么∠AOB 是多少度?
O
A
B
C
D
解:因为 :OB 平分∠AOC,
∠AOC=80°,
所以:
∠AOB= ∠AOC= ×80°=40°
(2) 如果∠AOD=100°,∠COD=20°,那么∠BOD是多少度?
O
A
B
C
D
所以∠BOD= ∠BOC+∠COD= 40°+ 20°= 60°
解:因为 ∠COD = 20°,
所以 ∠AOC= ∠AOD-∠COD
= 100°-20°= 80°
又因为 OB 平分∠AOC,
所以∠AOB= ∠AOC = ×80°= 40°
1.如图,AM为∠BAC的平分线,下列等式错误的是( )
A.∠BAM = ∠BAC
B.∠BAM = ∠CAM
C.∠BAM = 2∠CAM
D.2∠CAM = ∠BAC
C
2、若∠AOB=60°, ∠BOC=40°, 求∠AOC.
A
C
B
O
A
C
B
O
当堂巩固
课堂小结
线
段
的
运
算
与
比
较
线段的比较
线段的运算
角 的 比 较
角的运算
度 量 法
叠 合 法
线段和差
线段的计算
线段中点
角的
运
算
与
比
较
角的和差
角平分线
角的计算
课堂小结
D
C
A
B
2.如图∠AOE=120°,OC是∠AOE内部任意一条射线,OB,OE分别为∠AOC,∠COE的角平分线,求∠BOD
A
B
C
D
E
拓展延伸
1.如图,线段AE=10,C为线段AE上任意一点,D,B分别为AC,CE中点,求BD的长
O
A
B
C
D
E
谢谢!
