青岛版七下数学13.2.2多边形的内角和与外角和 课件(共17张ppt)
文档属性
| 名称 | 青岛版七下数学13.2.2多边形的内角和与外角和 课件(共17张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 752.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
13.2.2 多边形的内角和
1.探索并证明多边形内角和公式,体 会化归思想和从具体到抽象的研究问题的方法;
学习目标
2.掌握多边形内角和公式,并会运用
公式解决简单问题.
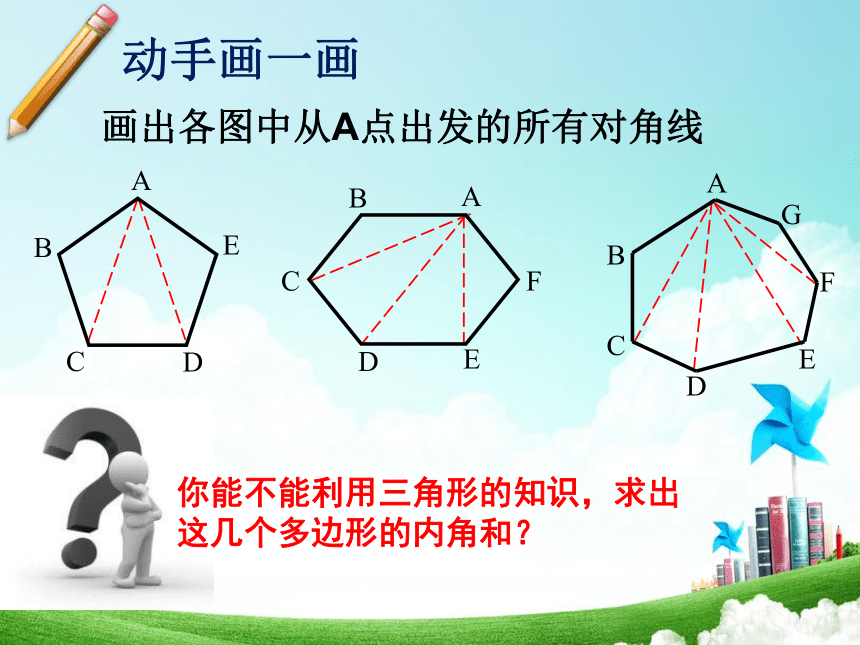
动手画一画
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
E
F
G
画出各图中从A点出发的所有对角线
你能不能利用三角形的知识,求出
这几个多边形的内角和?
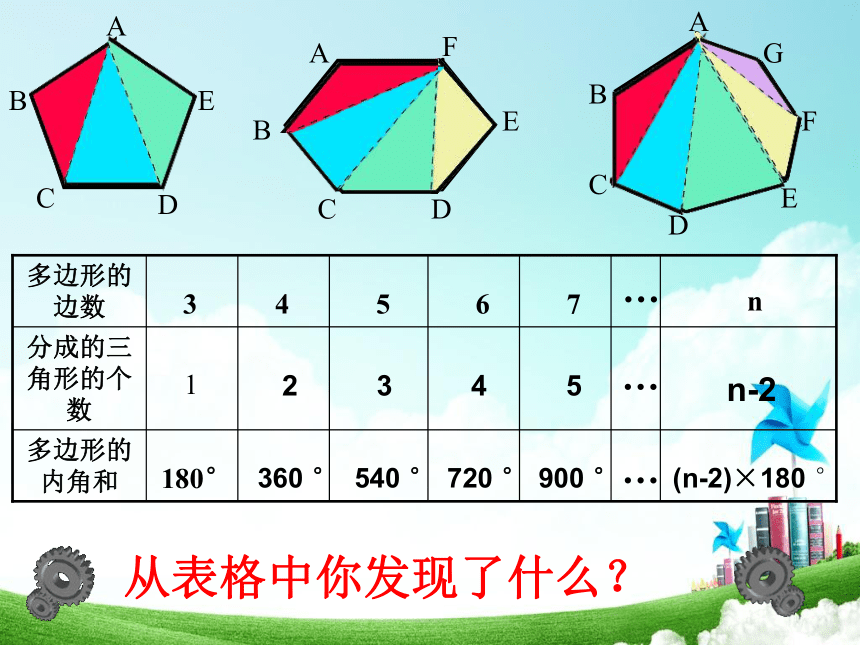
多边形的内角和
分成的三角形的个数
多边形的边数
3
4
5
6
7
…
n
A
B
C
D
E
A
B
C
D
E
F
G
A
B
C
D
E
F
1
…
2
3
4
5
n-2
180°
…
(n-2)×180 °
900 °
720 °
540 °
360 °
从表格中你发现了什么?
A
B
C
D
A
B
C
D
A
B
C
D
F
E
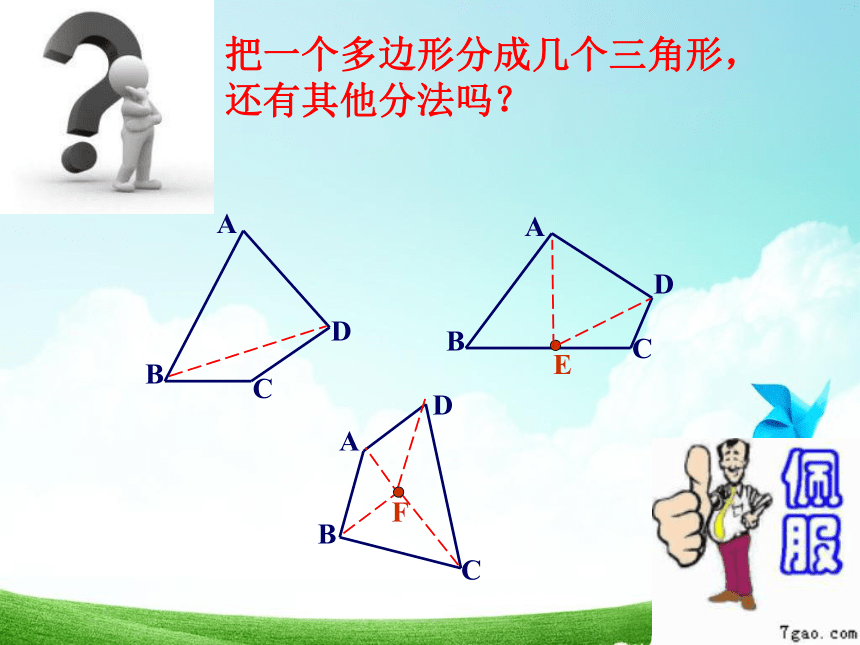
把一个多边形分成几个三角形,
还有其他分法吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
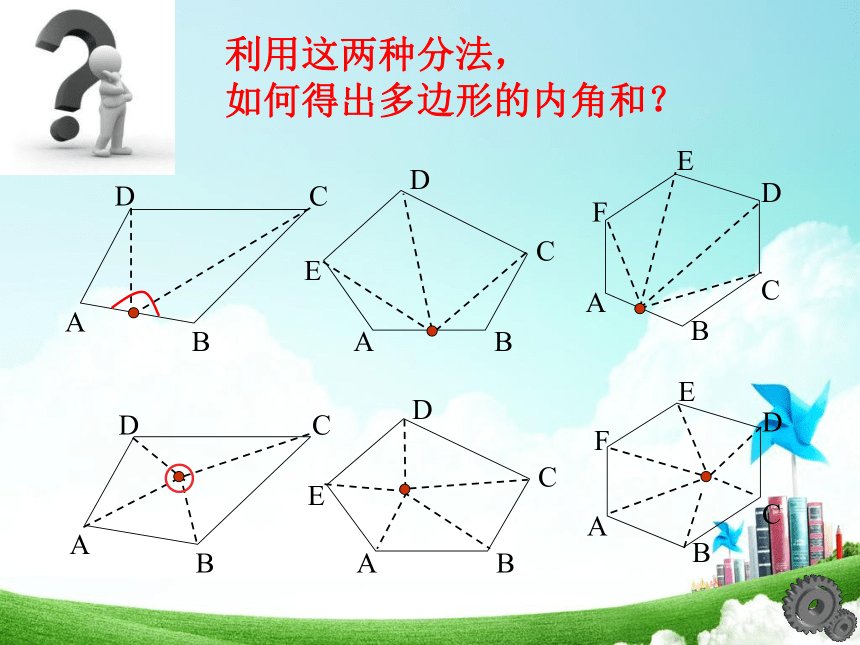
利用这两种分法,
如何得出多边形的内角和?
n边形的内角和等于
(n-2)·180°
多边形的内角和公式:
这里的字母n是指大于或等于3的正整数
我学习!我快乐!
(1)八边形的内角和是 ____。
(2)十边形的内角和是____。
(3)一个多边形的内角和是1800°,
它是 ________边形。
(8-2)×180o=1080o
(10-2)×180o=1440o
(n-2)×180o=1800o
n=12
我学习!我快乐!
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
C
B
D
解:如图,在四边形ABCD中,
∵ ∠A+∠B+∠C+∠D=360°
∠A+∠C=180 °
∴ ∠ B+∠D =360°-(∠A+∠C)
=360°-180°
=180°
如果四边形一组对角互补,
那么另一组对角也互补。
例题讲解
变式:如图,OB⊥AB,垂足为B,OC⊥AC,垂足为C,试判断∠A与∠1有什么关系?
C
A
B
O
1
例题变式
相等
D
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
F
E
C
B
A
6
1
2
3
4
5
分析:考虑一下问题:
(1)任何一个外角同与它相邻的内角有什么关系
(2)六边形的6个外角加上与它们相邻的内角,所得总和是多少?
(3)上述总和与六边形的内角和,外角和有什么关系?
练习这些问题,考虑外角和的求法.
解:六边形的任何一个外角加上它相邻的内角都等于180°。因此六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°
这个总和就是六边形的外角和加上内角和,所以外角和等于总和减去内角和,
即六边形的外角和等于
6×180°-(6-2)×180°=2×180°=360°
如果将例2中六边形换为n边形
(n是不小于3的任意整数),
可以得到同样结果吗?
多边形的外角和等于360°
一个正多边形的每一个内角都等于135°,则这个多边形是几边形?
解:设这个多边形是n边形,由题意得
(n-2)×180o=n × 135o
解得:n=8
∴这个多边形是八边形。
巩固提高
1、若一个多边形的内角和等于1080°,则这个多边形的边数是_______。
2、七边形的内角和等于_______。
3、正五边形的每个内角是________。
4、下列角度中,不能成为多边形的内角和的是( )
(A)540° (B)580° (C)1800° (D)900°
5、从n边形的一个顶点出发画对角线,最多可以画_____条,这些对角线把n边形分成_____个三角形。
当堂检测
8
900°
108°
B
n-3
n-2
①多边形的内角和公式:(n-2)·180°;
②多边形的外角和等于360°;
③用转化以及方程思想解决问题;
④由特殊到一般研究问题的方法.
回味无穷
如图,求∠A+∠B+∠C+∠D+∠E+∠F的值。
F
A
B
C
D
E
N
M
K
T
H
思考:
13.2.2 多边形的内角和
1.探索并证明多边形内角和公式,体 会化归思想和从具体到抽象的研究问题的方法;
学习目标
2.掌握多边形内角和公式,并会运用
公式解决简单问题.
动手画一画
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
E
F
G
画出各图中从A点出发的所有对角线
你能不能利用三角形的知识,求出
这几个多边形的内角和?
多边形的内角和
分成的三角形的个数
多边形的边数
3
4
5
6
7
…
n
A
B
C
D
E
A
B
C
D
E
F
G
A
B
C
D
E
F
1
…
2
3
4
5
n-2
180°
…
(n-2)×180 °
900 °
720 °
540 °
360 °
从表格中你发现了什么?
A
B
C
D
A
B
C
D
A
B
C
D
F
E
把一个多边形分成几个三角形,
还有其他分法吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
利用这两种分法,
如何得出多边形的内角和?
n边形的内角和等于
(n-2)·180°
多边形的内角和公式:
这里的字母n是指大于或等于3的正整数
我学习!我快乐!
(1)八边形的内角和是 ____。
(2)十边形的内角和是____。
(3)一个多边形的内角和是1800°,
它是 ________边形。
(8-2)×180o=1080o
(10-2)×180o=1440o
(n-2)×180o=1800o
n=12
我学习!我快乐!
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
A
C
B
D
解:如图,在四边形ABCD中,
∵ ∠A+∠B+∠C+∠D=360°
∠A+∠C=180 °
∴ ∠ B+∠D =360°-(∠A+∠C)
=360°-180°
=180°
如果四边形一组对角互补,
那么另一组对角也互补。
例题讲解
变式:如图,OB⊥AB,垂足为B,OC⊥AC,垂足为C,试判断∠A与∠1有什么关系?
C
A
B
O
1
例题变式
相等
D
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
F
E
C
B
A
6
1
2
3
4
5
分析:考虑一下问题:
(1)任何一个外角同与它相邻的内角有什么关系
(2)六边形的6个外角加上与它们相邻的内角,所得总和是多少?
(3)上述总和与六边形的内角和,外角和有什么关系?
练习这些问题,考虑外角和的求法.
解:六边形的任何一个外角加上它相邻的内角都等于180°。因此六边形的6个外角加上与它们相邻的内角,所得总和等于6×180°
这个总和就是六边形的外角和加上内角和,所以外角和等于总和减去内角和,
即六边形的外角和等于
6×180°-(6-2)×180°=2×180°=360°
如果将例2中六边形换为n边形
(n是不小于3的任意整数),
可以得到同样结果吗?
多边形的外角和等于360°
一个正多边形的每一个内角都等于135°,则这个多边形是几边形?
解:设这个多边形是n边形,由题意得
(n-2)×180o=n × 135o
解得:n=8
∴这个多边形是八边形。
巩固提高
1、若一个多边形的内角和等于1080°,则这个多边形的边数是_______。
2、七边形的内角和等于_______。
3、正五边形的每个内角是________。
4、下列角度中,不能成为多边形的内角和的是( )
(A)540° (B)580° (C)1800° (D)900°
5、从n边形的一个顶点出发画对角线,最多可以画_____条,这些对角线把n边形分成_____个三角形。
当堂检测
8
900°
108°
B
n-3
n-2
①多边形的内角和公式:(n-2)·180°;
②多边形的外角和等于360°;
③用转化以及方程思想解决问题;
④由特殊到一般研究问题的方法.
回味无穷
如图,求∠A+∠B+∠C+∠D+∠E+∠F的值。
F
A
B
C
D
E
N
M
K
T
H
思考:
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
