双曲线
图片预览



文档简介
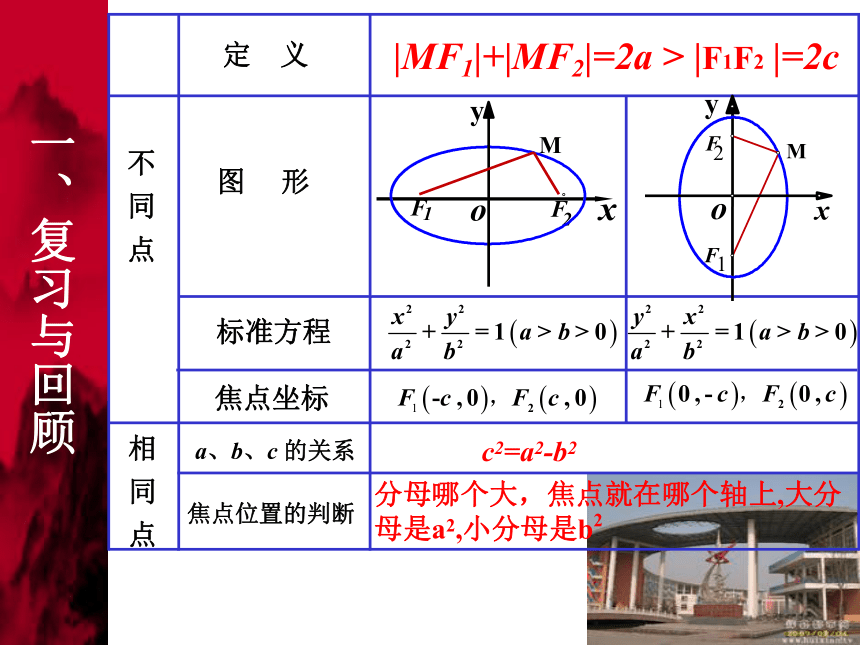
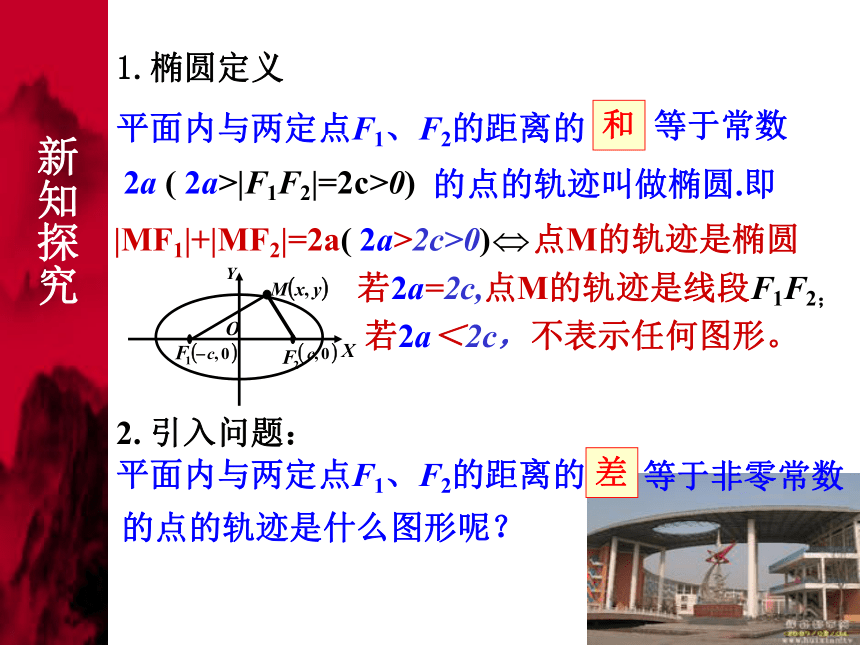
课件18张PPT。双曲线及其标准方程分母哪个大,焦点就在哪个轴上,大分母是a2,小分母是b2c2=a2-b2|MF1|+|MF2|=2a > |F1F2 |=2c 一、复习与回顾1.椭圆定义2. 引入问题:
|MF1|+|MF2|=2a( 2a>2c>0) 点M的轨迹是椭圆
若2a=2c,点M的轨迹是线段F1F2;
若2a<2c,不表示任何图形。
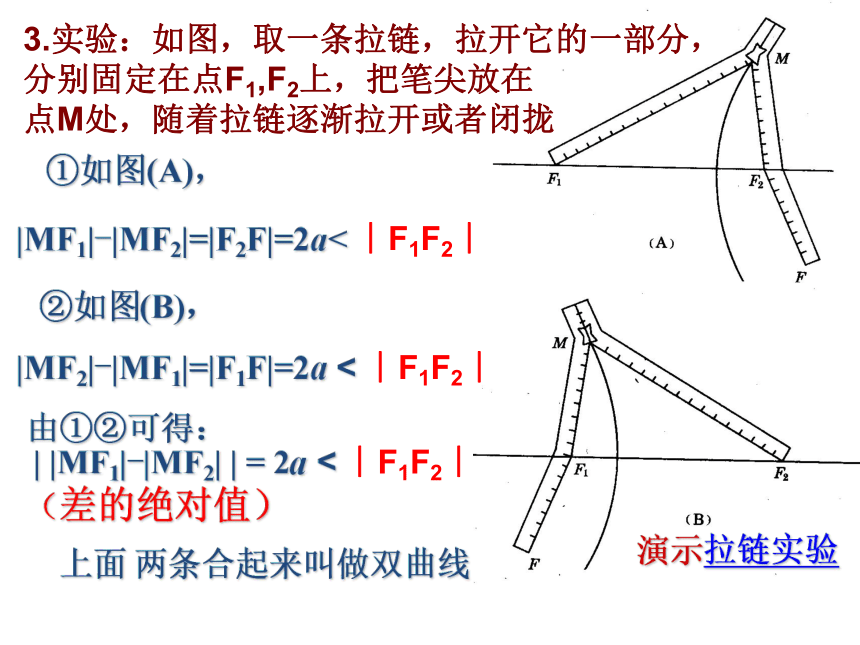
新知探究 |MF1|-|MF2|=|F2F|=2a< ︱F1F2︱②如图(B),上面 两条合起来叫做双曲线由①②可得: | |MF1|-|MF2| | = 2a < ︱F1F2︱
(差的绝对值) |MF2|-|MF1|=|F1F|=2a < ︱F1F2︱①如图(A),
3.实验:如图,取一条拉链,拉开它的一部分,
分别固定在点F1,F2上,把笔尖放在
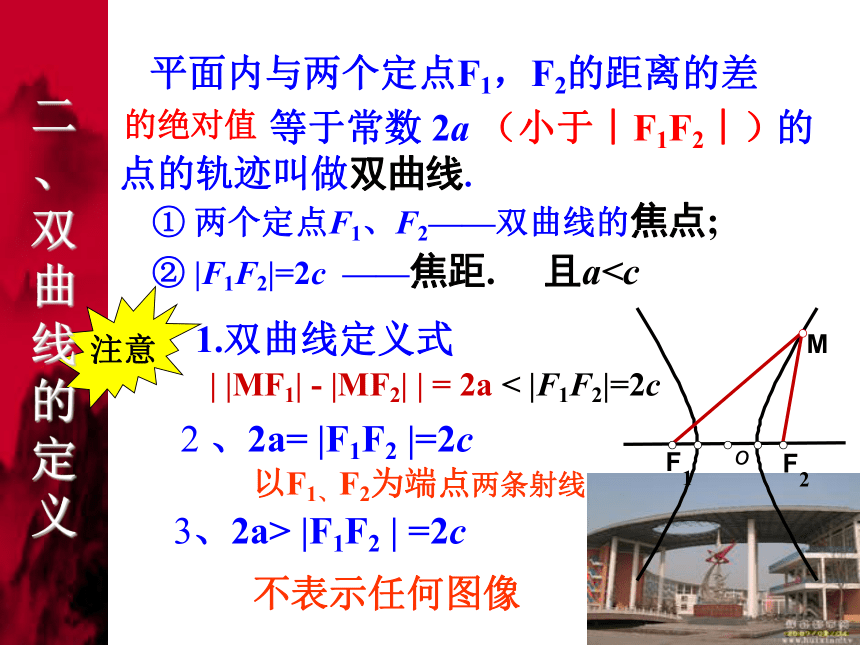
点M处,随着拉链逐渐拉开或者闭拢 演示拉链实验 ① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距. 且a 点的轨迹叫做双曲线.的绝对值2a (小于︱F1F2︱)注意1.双曲线定义式
2 、2a= |F1F2 |=2c以F1、F2为端点两条射线3、2a> |F1F2 | =2c 不表示任何图像二 、双曲线的定义| |MF1| - |MF2| | = 2a < |F1F2|=2cxo 设P(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数=2aF1F2P 以F1,F2所在的直线为X轴,线段F1F2的中点为原点建立直角
坐标系1. 建系.2.设点.3.列式.4.化简.三 、双曲线标准方程的推导 | |PF1|-|PF2| | = 2a<︱F1F2︱ 移项两边平方后整理得: 两边再平方后整理得: 由双曲线定义知: 设 代入上式整理得: 即:这就是焦点在x轴上的双曲线的标准
方程.若建系时,焦点在y轴上呢?| |MF1|-|MF2| | =2a<|F1F2|=2cF ( ±c, 0) F(0, ± c)四 、双曲线标准方程(1)F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,c2=a2-b2||MF1|-|MF2||=2a<2c |MF1|+|MF2|=2a>2cF(0,±c)F(0,±c)四 、椭圆与双曲线(2)例、请求出下列双曲线的 a、b、c和它们的焦点坐标。五 、例题解析分析:方程 表示双曲线时,则
m的取值范围是_________________.变式二:变式一:如果方程 表示双曲线,求 的取值范围.反思: 是否表示双曲线? 表示焦点在 轴上的双曲线;表示焦点在 轴上的双曲线。 例1、已知双曲线的焦点为F1(-5,0), F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于8,求双曲线的标准方程. ∵ 2a = 8, c=5∴ a = 4, c = 5∴ b2 = 52-42 =9所以所求双曲线的标准方程为:六 、典型例题1、已知 , 是椭圆 的两个焦点,平面内一个动点 满足
则动点 的轨迹是( )双曲线 B.双曲线的一个分支
C.两条射线 D. 一条射线D2、过双曲线 左焦点 的直线交双曲线的左支于 、 两点, 为其右焦点,则8 使A、B两点在x轴上,并且点O与线段AB的中点重合解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上. 例2.已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.如图所示,建立直角坐标系xOy,设爆炸点P的坐标为(x,y),则即 2a=680,a=340,因此炮弹爆炸点的轨迹方程为1.△ABC一边的两个端点是B(0,6)
和C(0,-6),另两边所在直线的斜率
之积是 ,求顶点A的轨迹.练习2:已知动圆 过定点 与圆
内切,求动圆圆心 的轨迹方程.1.若双曲线 上的点 到点 的距离是15,则点 到点 的距离是( )
A.7 B. 23 C. 5或25 D. 7或23七 、走向高考D2.若椭圆 和双曲线
有相同的焦点 、 ,点 为椭圆与双曲线
的公共点,则 等于( )
A. B. C. D.
A3.设 、 是双曲线 的两个焦点,点 在双曲线上,且 ,求 的面积______谢谢光临指导
|MF1|+|MF2|=2a( 2a>2c>0) 点M的轨迹是椭圆
若2a=2c,点M的轨迹是线段F1F2;
若2a<2c,不表示任何图形。
新知探究 |MF1|-|MF2|=|F2F|=2a< ︱F1F2︱②如图(B),上面 两条合起来叫做双曲线由①②可得: | |MF1|-|MF2| | = 2a < ︱F1F2︱
(差的绝对值) |MF2|-|MF1|=|F1F|=2a < ︱F1F2︱①如图(A),
3.实验:如图,取一条拉链,拉开它的一部分,
分别固定在点F1,F2上,把笔尖放在
点M处,随着拉链逐渐拉开或者闭拢 演示拉链实验 ① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距. 且a
2 、2a= |F1F2 |=2c以F1、F2为端点两条射线3、2a> |F1F2 | =2c 不表示任何图像二 、双曲线的定义| |MF1| - |MF2| | = 2a < |F1F2|=2cxo 设P(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)
常数=2aF1F2P 以F1,F2所在的直线为X轴,线段F1F2的中点为原点建立直角
坐标系1. 建系.2.设点.3.列式.4.化简.三 、双曲线标准方程的推导 | |PF1|-|PF2| | = 2a<︱F1F2︱ 移项两边平方后整理得: 两边再平方后整理得: 由双曲线定义知: 设 代入上式整理得: 即:这就是焦点在x轴上的双曲线的标准
方程.若建系时,焦点在y轴上呢?| |MF1|-|MF2| | =2a<|F1F2|=2cF ( ±c, 0) F(0, ± c)四 、双曲线标准方程(1)F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,c2=a2-b2||MF1|-|MF2||=2a<2c |MF1|+|MF2|=2a>2cF(0,±c)F(0,±c)四 、椭圆与双曲线(2)例、请求出下列双曲线的 a、b、c和它们的焦点坐标。五 、例题解析分析:方程 表示双曲线时,则
m的取值范围是_________________.变式二:变式一:如果方程 表示双曲线,求 的取值范围.反思: 是否表示双曲线? 表示焦点在 轴上的双曲线;表示焦点在 轴上的双曲线。 例1、已知双曲线的焦点为F1(-5,0), F2(5,0),双曲线上一点P到F1、F2的距离的差的绝对值等于8,求双曲线的标准方程. ∵ 2a = 8, c=5∴ a = 4, c = 5∴ b2 = 52-42 =9所以所求双曲线的标准方程为:六 、典型例题1、已知 , 是椭圆 的两个焦点,平面内一个动点 满足
则动点 的轨迹是( )双曲线 B.双曲线的一个分支
C.两条射线 D. 一条射线D2、过双曲线 左焦点 的直线交双曲线的左支于 、 两点, 为其右焦点,则8 使A、B两点在x轴上,并且点O与线段AB的中点重合解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上. 例2.已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.如图所示,建立直角坐标系xOy,设爆炸点P的坐标为(x,y),则即 2a=680,a=340,因此炮弹爆炸点的轨迹方程为1.△ABC一边的两个端点是B(0,6)
和C(0,-6),另两边所在直线的斜率
之积是 ,求顶点A的轨迹.练习2:已知动圆 过定点 与圆
内切,求动圆圆心 的轨迹方程.1.若双曲线 上的点 到点 的距离是15,则点 到点 的距离是( )
A.7 B. 23 C. 5或25 D. 7或23七 、走向高考D2.若椭圆 和双曲线
有相同的焦点 、 ,点 为椭圆与双曲线
的公共点,则 等于( )
A. B. C. D.
A3.设 、 是双曲线 的两个焦点,点 在双曲线上,且 ,求 的面积______谢谢光临指导
