安徽省桐城市第二中学2021-2022学年九年级上学期期中考试数学试题(Word版含图片答案)
文档属性
| 名称 | 安徽省桐城市第二中学2021-2022学年九年级上学期期中考试数学试题(Word版含图片答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 12:58:26 | ||
图片预览

文档简介
桐城二中2021-2022学年度第一学期期中学情调研考试
九年级数学
一、选择题(4分×10=40分)
1.抛物线的图像上两点A(m,3)、(n,3)、(m≠n),当x=m+n时,对应的函数值为( )
A.-1 B.3 C.0 D.无法确定
2.已知二次函数y=-4x+a,下列说法错误的是 ( )
A.当x<1时,y随x的增大而减小;
B.若图象与x轴有交点,则a≦4;
C.当a=3时,观察图象知不等式-4x+3>0的解集为1D.若将图象向上平移1个单位,再向左平移3个单位后过(1,-2),则a=-3
3.二次函数y=a+bx+c的图象如图所示,则一次函数y=bx+-4ac与反比例函数y=在同一坐标系内的图像大致为 ( )
A B C D
4.二次函数y=+mx的图象如图,关于x的一元二次方程+mx-t=0(t为实数)在1A.t>-5 B.-5C.35.下列各组中的四条线段成比例的是( )
A.a=,b=3,c=2,d=
B.a=4,b=6,c=5,d=10
C.a=2,b=3,c=4,d=1
D.a=2,b=,c=,d=
6.已知线段a,b,如果a:b=5:2,那么下列各式一定正确的是( )
A.. B. C. D.
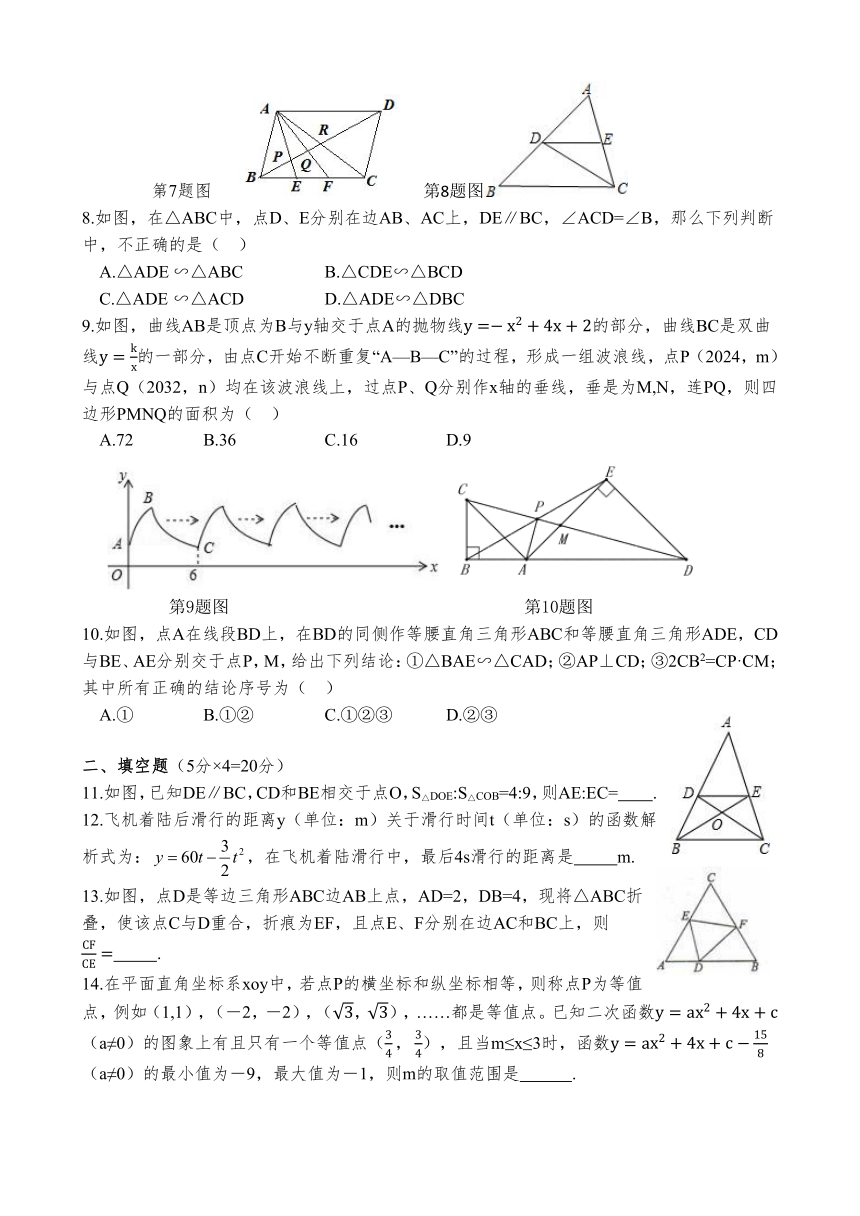
7.如图,在ABCD中,E、F分别是边BC上两个三等分点,B、D分别交AE、AF、AC于P、Q、R,则BP:PQ:QR=( )
A.3:2:1 B.5:3:2 C.6:5:4 D.5:4:3
第7题图 第8题图
8.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,∠ACD=∠B,那么下列判断中,不正确的是( )
A.△ADE ∽△ABC B.△CDE∽△BCD
C.△ADE ∽△ACD D.△ADE∽△DBC
9.如图,曲线AB是顶点为B与y轴交于点A的抛物线的部分,曲线BC是双曲线的一部分,由点C开始不断重复“A—B—C”的过程,形成一组波浪线,点P(2024,m)与点Q(2032,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂是为M,N,连PQ,则四边形PMNQ的面积为( )
A.72 B.36 C.16 D.9
第9题图 第10题图
10.如图,点A在线段BD上,在BD的同侧作等腰直角三角形ABC和等腰直角三角形ADE,CD与BE、AE分别交于点P,M,给出下列结论:①△BAE∽△CAD;②AP⊥CD;③2CB2=CP·CM;其中所有正确的结论序号为( )
A.① B.①② C.①②③ D.②③
二、填空题(5分×4=20分)
11.如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=4:9,则AE:EC= .
12.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式为:,在飞机着陆滑行中,最后4s滑行的距离是 m.
13.如图,点D是等边三角形ABC边AB上点,AD=2,DB=4,现将△ABC折叠,使该点C与D重合,折痕为EF,且点E、F分别在边AC和BC上,则 .
14.在平面直角坐标系xoy中,若点P的横坐标和纵坐标相等,则称点P为等值点,例如(1,1),(-2,-2),(,),……都是等值点。已知二次函数(a≠0)的图象上有且只有一个等值点(),且当m≤x≤3时,函数(a≠0)的最小值为-9,最大值为-1,则m的取值范围是 .
三、(每小题8分)
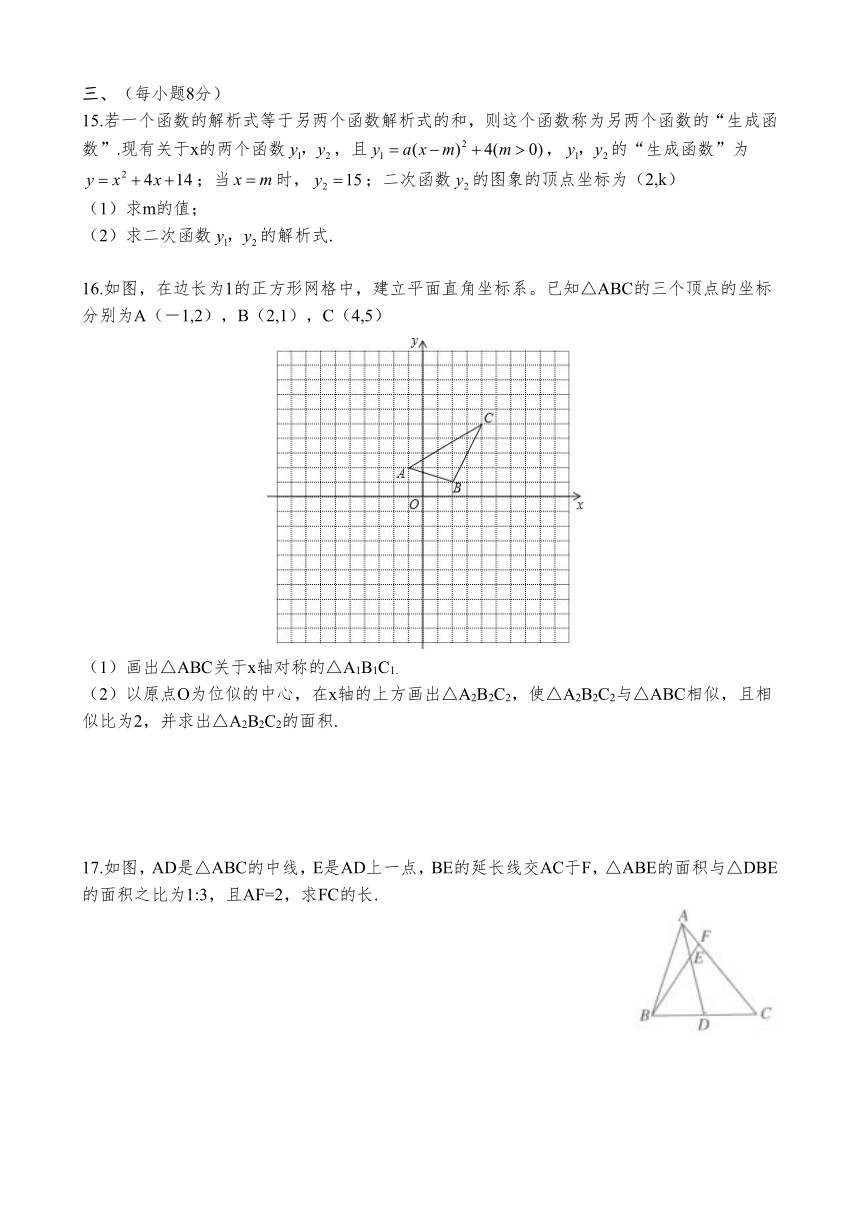
15.若一个函数的解析式等于另两个函数解析式的和,则这个函数称为另两个函数的“生成函数”.现有关于x的两个函数,且,的“生成函数”为;当时,;二次函数的图象的顶点坐标为(2,k)
(1)求m的值;
(2)求二次函数的解析式.
16.如图,在边长为1的正方形网格中,建立平面直角坐标系。已知△ABC的三个顶点的坐标分别为A(-1,2),B(2,1),C(4,5)
(1)画出△ABC关于x轴对称的△A1B1C1.
(2)以原点O为位似的中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC相似,且相似比为2,并求出△A2B2C2的面积.
17.如图,AD是△ABC的中线,E是AD上一点,BE的延长线交AC于F,△ABE的面积与△DBE的面积之比为1:3,且AF=2,求FC的长.
18.如图,直线与反比例函数交于A(1,4),B两点,延长AO交反比例函数图象于点C,连OB.
(1)求k、b;
(2)写出一次函数值小于反比例函数值的x的取值范围;
(3)在y轴上是否存在一点P,使?若存在,求出点P坐标,若不存在,请说明理由.
19.如图,①已知D、E分别为△ABC边AB、AC上一点,DE∥BC,连CD、BE、CD、BE相交于点F,连AF并延长分别交DE、BC于点H,G.
(1)求证:G为BC中点;
(2)如图②,只用一把无刻度的直尺画出矩形ABCD的一条对称轴.
20.如图,在△ABC中,点D的边BC上,连接AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且AD2=DE·DF.
(1)求证:△BFD∽△CAD;
(2)求证:BF·DE=AB·AD.
21.如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开了桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即ED的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上数据求出DE的长度.(结果保留根号)
22.某口罩生产商自二月份以来,一直积极恢复产能,每日口罩生产量y(百万个)与天数x(1≤x≤29,且x为整数)的函数图象如图所示,该生产商对口供应市场对口罩的需求量Z(百万个)与天数x呈抛物线型,第一天市场口罩缺口(需求量与供应量差)就达到7.5(百万个),之后若干天,市场口罩需求量不断上升,在第10天需求量达到最高峰60(百万个).
(1)求出y与x的函数关系式;
(2)当市场供应量不小于需求量时,市民买口罩才无须提前预约,在整个2月份,市民无须预约即可购买口罩共有多少天?
23.如图,已知在△ABC中,AB=AC=a,BC=10,动点P沿CA方向从点C向终点A运动,同时,动点Q沿CB方向从点C向终点B运动,速度都为每秒1个单位,P,Q中任一点到达终点时,另一点也随之停止运动,过点P作PD∥BC,交AB边于点D,连接DQ,设P、Q的运动时间为t秒.
(1)直接写出BD的长.(用含t的代数式表示)
(2)若a=15,则当t为何值时,△ADP与△BDQ相似?
(3)是否存在某个a的值,使点P,Q在运动过程中,存在S△BDQ :S△ADP:S梯形CPDQ=1:4:4?若存在,请求出a的值;若不存在,请说明理由.
九年级数学
一、选择题(4分×10=40分)
1.抛物线的图像上两点A(m,3)、(n,3)、(m≠n),当x=m+n时,对应的函数值为( )
A.-1 B.3 C.0 D.无法确定
2.已知二次函数y=-4x+a,下列说法错误的是 ( )
A.当x<1时,y随x的增大而减小;
B.若图象与x轴有交点,则a≦4;
C.当a=3时,观察图象知不等式-4x+3>0的解集为1
3.二次函数y=a+bx+c的图象如图所示,则一次函数y=bx+-4ac与反比例函数y=在同一坐标系内的图像大致为 ( )
A B C D
4.二次函数y=+mx的图象如图,关于x的一元二次方程+mx-t=0(t为实数)在1
A.a=,b=3,c=2,d=
B.a=4,b=6,c=5,d=10
C.a=2,b=3,c=4,d=1
D.a=2,b=,c=,d=
6.已知线段a,b,如果a:b=5:2,那么下列各式一定正确的是( )
A.. B. C. D.
7.如图,在ABCD中,E、F分别是边BC上两个三等分点,B、D分别交AE、AF、AC于P、Q、R,则BP:PQ:QR=( )
A.3:2:1 B.5:3:2 C.6:5:4 D.5:4:3
第7题图 第8题图
8.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,∠ACD=∠B,那么下列判断中,不正确的是( )
A.△ADE ∽△ABC B.△CDE∽△BCD
C.△ADE ∽△ACD D.△ADE∽△DBC
9.如图,曲线AB是顶点为B与y轴交于点A的抛物线的部分,曲线BC是双曲线的一部分,由点C开始不断重复“A—B—C”的过程,形成一组波浪线,点P(2024,m)与点Q(2032,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂是为M,N,连PQ,则四边形PMNQ的面积为( )
A.72 B.36 C.16 D.9
第9题图 第10题图
10.如图,点A在线段BD上,在BD的同侧作等腰直角三角形ABC和等腰直角三角形ADE,CD与BE、AE分别交于点P,M,给出下列结论:①△BAE∽△CAD;②AP⊥CD;③2CB2=CP·CM;其中所有正确的结论序号为( )
A.① B.①② C.①②③ D.②③
二、填空题(5分×4=20分)
11.如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=4:9,则AE:EC= .
12.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式为:,在飞机着陆滑行中,最后4s滑行的距离是 m.
13.如图,点D是等边三角形ABC边AB上点,AD=2,DB=4,现将△ABC折叠,使该点C与D重合,折痕为EF,且点E、F分别在边AC和BC上,则 .
14.在平面直角坐标系xoy中,若点P的横坐标和纵坐标相等,则称点P为等值点,例如(1,1),(-2,-2),(,),……都是等值点。已知二次函数(a≠0)的图象上有且只有一个等值点(),且当m≤x≤3时,函数(a≠0)的最小值为-9,最大值为-1,则m的取值范围是 .
三、(每小题8分)
15.若一个函数的解析式等于另两个函数解析式的和,则这个函数称为另两个函数的“生成函数”.现有关于x的两个函数,且,的“生成函数”为;当时,;二次函数的图象的顶点坐标为(2,k)
(1)求m的值;
(2)求二次函数的解析式.
16.如图,在边长为1的正方形网格中,建立平面直角坐标系。已知△ABC的三个顶点的坐标分别为A(-1,2),B(2,1),C(4,5)
(1)画出△ABC关于x轴对称的△A1B1C1.
(2)以原点O为位似的中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC相似,且相似比为2,并求出△A2B2C2的面积.
17.如图,AD是△ABC的中线,E是AD上一点,BE的延长线交AC于F,△ABE的面积与△DBE的面积之比为1:3,且AF=2,求FC的长.
18.如图,直线与反比例函数交于A(1,4),B两点,延长AO交反比例函数图象于点C,连OB.
(1)求k、b;
(2)写出一次函数值小于反比例函数值的x的取值范围;
(3)在y轴上是否存在一点P,使?若存在,求出点P坐标,若不存在,请说明理由.
19.如图,①已知D、E分别为△ABC边AB、AC上一点,DE∥BC,连CD、BE、CD、BE相交于点F,连AF并延长分别交DE、BC于点H,G.
(1)求证:G为BC中点;
(2)如图②,只用一把无刻度的直尺画出矩形ABCD的一条对称轴.
20.如图,在△ABC中,点D的边BC上,连接AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且AD2=DE·DF.
(1)求证:△BFD∽△CAD;
(2)求证:BF·DE=AB·AD.
21.如图,小华和同伴在春游期间,发现在某地小山坡的点E处有一棵盛开了桃花的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即ED的长度,小华站在点B的位置,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小华的身高为1.8米,请你利用以上数据求出DE的长度.(结果保留根号)
22.某口罩生产商自二月份以来,一直积极恢复产能,每日口罩生产量y(百万个)与天数x(1≤x≤29,且x为整数)的函数图象如图所示,该生产商对口供应市场对口罩的需求量Z(百万个)与天数x呈抛物线型,第一天市场口罩缺口(需求量与供应量差)就达到7.5(百万个),之后若干天,市场口罩需求量不断上升,在第10天需求量达到最高峰60(百万个).
(1)求出y与x的函数关系式;
(2)当市场供应量不小于需求量时,市民买口罩才无须提前预约,在整个2月份,市民无须预约即可购买口罩共有多少天?
23.如图,已知在△ABC中,AB=AC=a,BC=10,动点P沿CA方向从点C向终点A运动,同时,动点Q沿CB方向从点C向终点B运动,速度都为每秒1个单位,P,Q中任一点到达终点时,另一点也随之停止运动,过点P作PD∥BC,交AB边于点D,连接DQ,设P、Q的运动时间为t秒.
(1)直接写出BD的长.(用含t的代数式表示)
(2)若a=15,则当t为何值时,△ADP与△BDQ相似?
(3)是否存在某个a的值,使点P,Q在运动过程中,存在S△BDQ :S△ADP:S梯形CPDQ=1:4:4?若存在,请求出a的值;若不存在,请说明理由.
同课章节目录
