必修5第一章解三角形1.1 正弦定理和余弦定理1.2 应用举例(word版含答案)
文档属性
| 名称 | 必修5第一章解三角形1.1 正弦定理和余弦定理1.2 应用举例(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 185.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-16 00:00:00 | ||
图片预览


文档简介
1.2 应用举例
一、选择题(共10小题;共50分)
1. 如图,在河岸 测量河宽 时,测量下列四组数据较适宜的是
A. 和 B. 和 C. 和 D. 和
2. 海上两个小岛 、 到海洋观察站 的距离都是 ,小岛 在观察站 北偏东 ,小岛 在观察站 南偏东 ,则 与 的距离是
A. B. C. D.
3. 美国为了加强对伊拉克的控制,进行了战略部署,在位于科威特和沙特的两个距离 的军事基地 和 ,测得伊拉克两支精锐部队分别在 处和 处,且 ,,,,如图所示,则伊军这两支精锐部队间的距离是
A. B. C. D.
4. 如图,从地面上 , 两点望山顶 ,测得它们的仰角分别为 和 ,已知 米,点 位于 上,则山高 等于
A. 米 B. 米 C. 米 D. 米
5. 某人驾驶一艘小游艇位于湖面 处,测得岸边一座电视塔的塔底在北偏东 方向,且塔顶的仰角为 ,此人驾驶游艇向正东方向行驶 米后到达 处,此时测得塔底位于北偏西 方向,则该塔的高度约为
A. 米 B. 米 C. 米 D. 米
6. 在 米高的楼顶测得对面一塔吊顶部的仰角为 ,塔基的俯角为 ,那么这座塔吊的高度是
A. B. C. D.
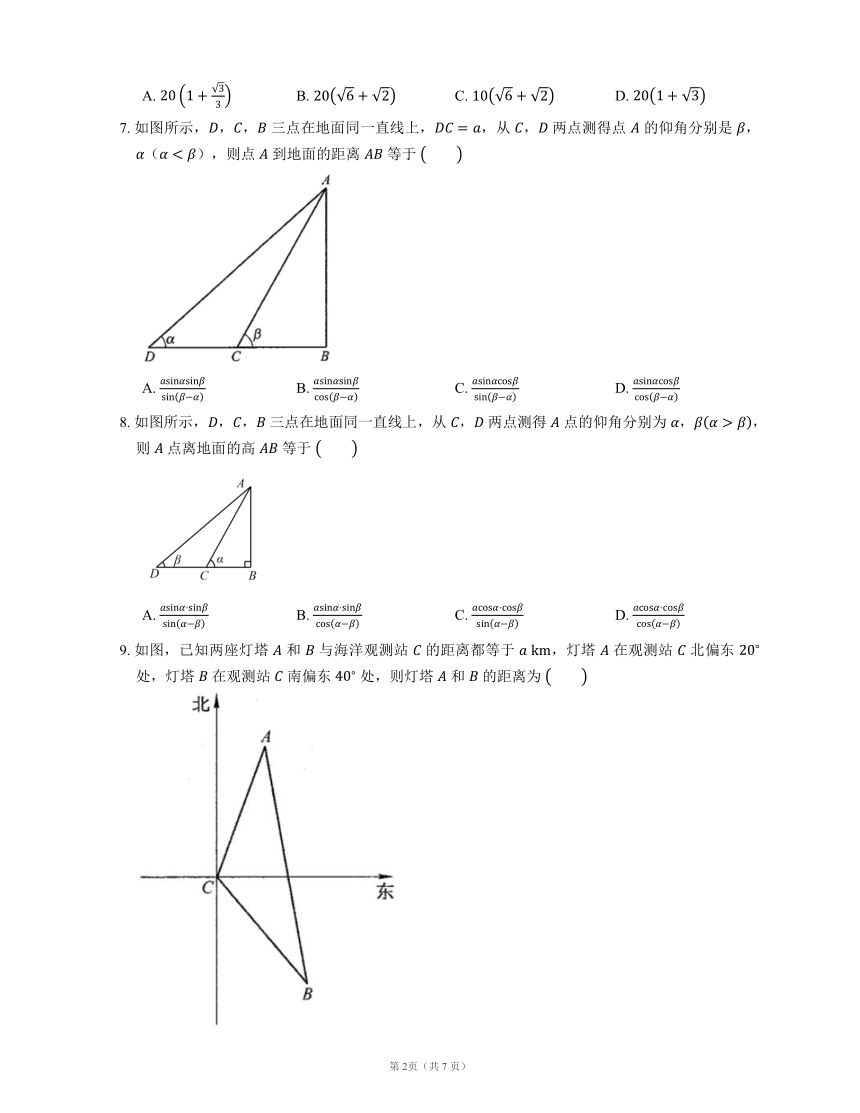
7. 如图所示,,, 三点在地面同一直线上,,从 , 两点测得点 的仰角分别是 ,(),则点 到地面的距离 等于
A. B. C. D.
8. 如图所示,,, 三点在地面同一直线上,从 , 两点测得 点的仰角分别为 ,,则 点离地面的高 等于
A. B. C. D.
9. 如图,已知两座灯塔 和 与海洋观测站 的距离都等于 ,灯塔 在观测站 北偏东 处,灯塔 在观测站 南偏东 处,则灯塔 和 的距离为
A. B. C. D.
10. 某船从 处向北偏东 方向航行 千米后到达 处,然后朝南偏西 的方向航行 千米到达 处,则 处与 处之间的距离为
A. 千米 B. 千米 C. 千米 D. 千米
二、填空题(共5小题;共25分)
11. 已知 、 两地的距离为 , 、 两地的距离为 ,现测得 ,则 、 两地的距离为 .
12. 在半径为 的圆形广场中央上空,置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为 ,若光源恰好照亮整个广场,则其高度应为 . (精确到 )
13. 如图所示,某住宅小区的平面图呈圆心角为 的扇形 , 是该小区的一个出入口,且小区里有一条平行于 的小路 .已知某人从 沿 走到 用了 分钟,从 沿着 走到 用了 分钟.若此人步行的速度为每分钟 米,则该扇形的半径为 米.
14. 如图所示,为测量山高 ,选择 和另一座山的山顶 为测量观测点,从 点测得 点的仰角 , 点的仰角 以及 ,从 点测得 ,已知山高 ,则山高 .
15. 河水的流速为 ,一艘小船想以垂直于河岸方向 的速度驶向对岸,则小船的静水速度为 .
三、解答题(共3小题;共39分)
16. 某地某时台风中心在甲地的东偏南 方向 千米处,经过 小时后,测得台风中心在甲地东偏南 方向 千米处.求台风移动的平均速度(结果保留两位小数).
17. 图如所示,游客从某旅游景区的景点 处下山至 处有两种路径.一种是从 沿直线步行到 ,另一种是先从 沿索道乘缆车到 ,然后从 沿直线步行到 .现有甲、乙两位游客从 处下山,甲沿 匀速步行,速度为 ,在甲出发 后,乙从 乘缆车到 ,在 处停留 后,再从匀速步行到 .假设缆车匀速直线运动的速度为 ,山路 长为 ,经测量 ,.
(1)求索道 的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短
(3)为使两位游客在 处互相等待的时间不超过 分钟,乙步行的速度应该控制在什么范围内
18. 如题所示:扇形 是一块半径为 千米,圆心角为 的风景区, 点在弧 上,现欲在风景区中规划三条三条商业街道 ,,,要求街道 与 垂直,街道 与 垂直,直线 表示第三条街道.
(1)如果 位于弧 的中点,求三条街道的总长度;
(2)由于环境的原因,三条街道 ,, 每年能产生的经济效益分别为每千米 万元、 万元及 万元,问:这三条街道每年能产生的经济总效益最高为多少 (精确到 万元)
答案
第一部分
1. D
2. B
3. A 【解析】因为 ,所以 是等边三角形.所以 .
在 中,由正弦定理,得 ,所以 .
所以在 中,由余弦定理,得 ,所以 .
4. D 【解析】设 ,则由题意,,,
在 中,,
在 中,,
所以 ,即 ,解得 .
所以山 的高度为 米.
5. C
6. D 【解析】由题意, 米,,,可知 是正方形,由此易得 米.再由 ,在直角三角形 中可求得 ,所以塔高为 .
7. A
8. A
9. B
10. B
第二部分
11.
12.
13.
【解析】由条件可知 米, 米.且 ,在 中,,所以 (米).
14.
【解析】在 中,,
在 中,,解得 ,
在 中,,
故 ,即山高 为 .
15.
【解析】为了使航向垂直河岸,船头必须斜向上游方向,
即:静水速度 斜向上游方向,河水速度 平行于河岸;
静水速度与河水速度的合速度 指向对岸.
所以静水速度 .
第三部分
16. 设台风经过的距离为 ,
则有 ,
.
平均速度 (千米/时).
17. (1) 因为 ,,
所以 ,
所以 ,,
所以 ,
由 ,得 .
(2) 设乙出发 分钟后,甲与乙的距离为 ,
则 ,
所以 ,
因为 ,
即 ,
所以 时,即乙出发 分钟后,乙在缆车上与甲的距离最短.
(3) 由正弦定理 ,
得 ,
乙从 出发时,甲已经走了 ,还需走 ,才能到达 ,
设乙的步行速度为 ,则 ,
所以 ,
解得 ,
所以为使两位游客在 处互相等待的时间不超过 分钟,乙步行的速度应控制在 范围内.
18. (1) .
(2) 万元.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 如图,在河岸 测量河宽 时,测量下列四组数据较适宜的是
A. 和 B. 和 C. 和 D. 和
2. 海上两个小岛 、 到海洋观察站 的距离都是 ,小岛 在观察站 北偏东 ,小岛 在观察站 南偏东 ,则 与 的距离是
A. B. C. D.
3. 美国为了加强对伊拉克的控制,进行了战略部署,在位于科威特和沙特的两个距离 的军事基地 和 ,测得伊拉克两支精锐部队分别在 处和 处,且 ,,,,如图所示,则伊军这两支精锐部队间的距离是
A. B. C. D.
4. 如图,从地面上 , 两点望山顶 ,测得它们的仰角分别为 和 ,已知 米,点 位于 上,则山高 等于
A. 米 B. 米 C. 米 D. 米
5. 某人驾驶一艘小游艇位于湖面 处,测得岸边一座电视塔的塔底在北偏东 方向,且塔顶的仰角为 ,此人驾驶游艇向正东方向行驶 米后到达 处,此时测得塔底位于北偏西 方向,则该塔的高度约为
A. 米 B. 米 C. 米 D. 米
6. 在 米高的楼顶测得对面一塔吊顶部的仰角为 ,塔基的俯角为 ,那么这座塔吊的高度是
A. B. C. D.
7. 如图所示,,, 三点在地面同一直线上,,从 , 两点测得点 的仰角分别是 ,(),则点 到地面的距离 等于
A. B. C. D.
8. 如图所示,,, 三点在地面同一直线上,从 , 两点测得 点的仰角分别为 ,,则 点离地面的高 等于
A. B. C. D.
9. 如图,已知两座灯塔 和 与海洋观测站 的距离都等于 ,灯塔 在观测站 北偏东 处,灯塔 在观测站 南偏东 处,则灯塔 和 的距离为
A. B. C. D.
10. 某船从 处向北偏东 方向航行 千米后到达 处,然后朝南偏西 的方向航行 千米到达 处,则 处与 处之间的距离为
A. 千米 B. 千米 C. 千米 D. 千米
二、填空题(共5小题;共25分)
11. 已知 、 两地的距离为 , 、 两地的距离为 ,现测得 ,则 、 两地的距离为 .
12. 在半径为 的圆形广场中央上空,置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为 ,若光源恰好照亮整个广场,则其高度应为 . (精确到 )
13. 如图所示,某住宅小区的平面图呈圆心角为 的扇形 , 是该小区的一个出入口,且小区里有一条平行于 的小路 .已知某人从 沿 走到 用了 分钟,从 沿着 走到 用了 分钟.若此人步行的速度为每分钟 米,则该扇形的半径为 米.
14. 如图所示,为测量山高 ,选择 和另一座山的山顶 为测量观测点,从 点测得 点的仰角 , 点的仰角 以及 ,从 点测得 ,已知山高 ,则山高 .
15. 河水的流速为 ,一艘小船想以垂直于河岸方向 的速度驶向对岸,则小船的静水速度为 .
三、解答题(共3小题;共39分)
16. 某地某时台风中心在甲地的东偏南 方向 千米处,经过 小时后,测得台风中心在甲地东偏南 方向 千米处.求台风移动的平均速度(结果保留两位小数).
17. 图如所示,游客从某旅游景区的景点 处下山至 处有两种路径.一种是从 沿直线步行到 ,另一种是先从 沿索道乘缆车到 ,然后从 沿直线步行到 .现有甲、乙两位游客从 处下山,甲沿 匀速步行,速度为 ,在甲出发 后,乙从 乘缆车到 ,在 处停留 后,再从匀速步行到 .假设缆车匀速直线运动的速度为 ,山路 长为 ,经测量 ,.
(1)求索道 的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短
(3)为使两位游客在 处互相等待的时间不超过 分钟,乙步行的速度应该控制在什么范围内
18. 如题所示:扇形 是一块半径为 千米,圆心角为 的风景区, 点在弧 上,现欲在风景区中规划三条三条商业街道 ,,,要求街道 与 垂直,街道 与 垂直,直线 表示第三条街道.
(1)如果 位于弧 的中点,求三条街道的总长度;
(2)由于环境的原因,三条街道 ,, 每年能产生的经济效益分别为每千米 万元、 万元及 万元,问:这三条街道每年能产生的经济总效益最高为多少 (精确到 万元)
答案
第一部分
1. D
2. B
3. A 【解析】因为 ,所以 是等边三角形.所以 .
在 中,由正弦定理,得 ,所以 .
所以在 中,由余弦定理,得 ,所以 .
4. D 【解析】设 ,则由题意,,,
在 中,,
在 中,,
所以 ,即 ,解得 .
所以山 的高度为 米.
5. C
6. D 【解析】由题意, 米,,,可知 是正方形,由此易得 米.再由 ,在直角三角形 中可求得 ,所以塔高为 .
7. A
8. A
9. B
10. B
第二部分
11.
12.
13.
【解析】由条件可知 米, 米.且 ,在 中,,所以 (米).
14.
【解析】在 中,,
在 中,,解得 ,
在 中,,
故 ,即山高 为 .
15.
【解析】为了使航向垂直河岸,船头必须斜向上游方向,
即:静水速度 斜向上游方向,河水速度 平行于河岸;
静水速度与河水速度的合速度 指向对岸.
所以静水速度 .
第三部分
16. 设台风经过的距离为 ,
则有 ,
.
平均速度 (千米/时).
17. (1) 因为 ,,
所以 ,
所以 ,,
所以 ,
由 ,得 .
(2) 设乙出发 分钟后,甲与乙的距离为 ,
则 ,
所以 ,
因为 ,
即 ,
所以 时,即乙出发 分钟后,乙在缆车上与甲的距离最短.
(3) 由正弦定理 ,
得 ,
乙从 出发时,甲已经走了 ,还需走 ,才能到达 ,
设乙的步行速度为 ,则 ,
所以 ,
解得 ,
所以为使两位游客在 处互相等待的时间不超过 分钟,乙步行的速度应控制在 范围内.
18. (1) .
(2) 万元.
第1页(共1 页)
