8.2.1《代入法》课件(共31张PPT)
文档属性
| 名称 | 8.2.1《代入法》课件(共31张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 09:45:30 | ||
图片预览











文档简介
(共31张PPT)
代入法
人教版数学 七年级下册
学习目标
01
学习目标
会用代入消元法解简单的二元一次方程组。
理解解二元一次方程组的思路是“消元”, 经历从未知向已知转化的过程,体会化归思想。
新课教学
02
含有两个未知数,并且含有未知数的项的次数都是 1 的方程
什么叫做二元一次方程?
有两个未知数,含有每个未知数的项的次数都是 1,并且一共有两个方程的方程组
什么叫做二元一次方程组?
知识回顾
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
知识回顾
上节课我们学习了二元一次方程组和二元一次方程组的解,那给出一个一般的二元一次方程组,我们怎么得到它的解呢?本节课我们将学习解二元一次方程组的方法.
新课引入
知识点:用代入法解二元一次方程组
解:设胜 x 场,负 y 场.
则
篮球联赛中,每场都要分出胜负,每队胜 1 场得 2 分,负 1 场得 1 分. 某队 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
你能根据问题中的等量关系列出二元一次方程组吗?
新知讲解
解:设胜 x 场,则负 (10-x) 场.
则 2x+(10-x)=16.
这个实际问题能列一元一次方程求解吗?
篮球联赛中,每场都要分出胜负,每队胜 1 场得 2 分,负 1 场得 1 分. 某队 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
新知讲解
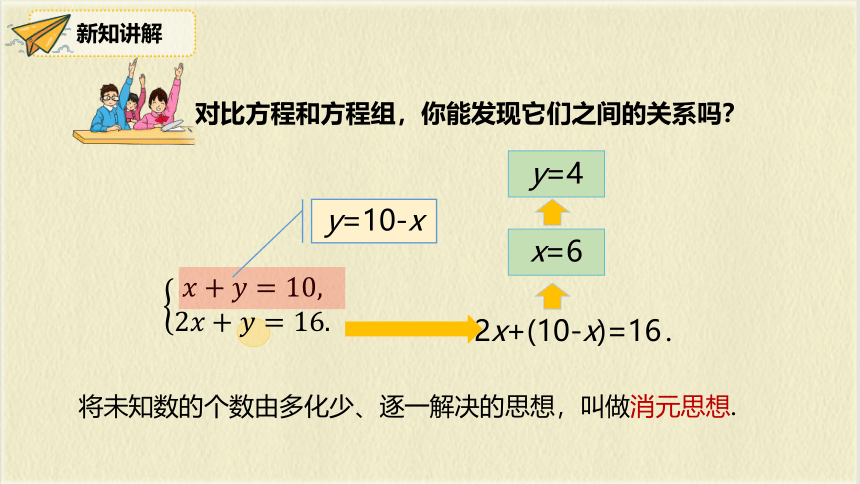
对比方程和方程组,你能发现它们之间的关系吗?
2x+(10-x)=16.
y=10-x
将未知数的个数由多化少、逐一解决的思想,叫做消元思想.
x=6
y=4
新知讲解
解二元一次方程组的基本思路:“消元”
二元一次方程组
一元一次方程
消元
转化
把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做代入消元法,简称代入法.
新知讲解
对于二元一次方程组
代入①或代入②可不可以?哪种运算更简便?
解:由①,得 y=10-x,③
把③代入②,得 2x+10-x=16,
解这个方程得 x=6.
①
②
把 x=6 代入③,得 y=4.
这个方程组的解是
答:这个队胜 6 场、负 4 场.
2.怎样求出 y ?
1.你能写出求 x 的过程吗?
新知讲解
用代入消元法解二元一次方程组的步骤:
1.变形
选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数.
把 y=ax+b (或 x=ay+b) 代入另一个没有变形的方程.
2.代入
3.求解
解消元后的一元一次方程.
4.回代
把求得的未知数的值代入步骤1中变形后的方程.
5.写解
把两个未知数的值用大括号联立起来.
新知讲解
三类代入消元法
(1)直接代入:方程组中含有用一个未知数表示另一个未知数的形式的方程;
(2)变形代入:方程组中含有未知数的系数为1或-1的方程;
(3)整体代入:方程组中某一未知数的系数成倍数关系.
新知讲解
例1 用代入法解方程组
变形
代入
求解
回代
写解
①
②
所以这个方程组的解是
把 y=-1代入③,得 x=2.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x=y+3 .③
解这个方程,得 y=-1.
新知讲解
例1 用代入法解方程组
变形
代入
求解
回代
写解
①
②
所以这个方程组的解是
把 y=-1代入③,得 x=2.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x=y+3 .③
解这个方程,得 y=-1.
新知讲解
例1 用代入法解方程组
变形
代入
求解
回代
写解
①
②
所以这个方程组的解是
把 y=-1代入③,得 x=2.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x=y+3 .③
解这个方程,得 y=-1.
新知讲解
二
元
一
次
方
程
组
x-y=3
3x-8y=14
y=-1
x = 2
解得 y
变形
解得 x
消去 x
一元一次方程
3(y+3)-8y=14
x =y+3
用y+3代替x,消未知数x.
用代入法解方程组:
代入
新知讲解
小试牛刀
03
1.用代入法解方程组 时,代入正确的是( )
A. x-2-x=4
B. x-2-2x=4
C. x-2+2x=4
D. x-2+x=4
x-2(1-x)=4
x-2+2x=4
C
小试牛刀
2.解方程组
①
②
所以这个方程组的解是
把 x=1 代入③,得 y=3-2=1.
把③代入②,得 9x+8(3x-2)=17.
解:由①,得 y=3x-2. ③
解这个方程,得 x=1.
小试牛刀
3.解方程组
①
②
所以这个方程组的解是
把 y=2 代入③,得 .
把③代入②,得 .
解:由①,得 .③
解这个方程,得 y=2.
小试牛刀
4.解方程组
解得 x=3.
把 y=2 代入③,得 2x=16-5×2=6.
把③代入②,得 4(16-5y)-7y=10.
解:由①,得 2x=16-5y. ③
解这个方程,得 y=2.
①
②
所以这个方程组的解是
小试牛刀
5.解方程组
把 x=2 代入①,得 y=1.
解:把①代入②,得 5x-3×3=1.
解这个方程,得 x=2.
①
②
所以这个方程组的解是
小试牛刀
延伸拓展
04
1.已知 |a+2b+3|+(3a-b-5)2=0,则(3a+2b)2020=___.
1
解析:∵|a+2b+3|≥0,(3a-b-5)2 ≥0, |a+2b+3|+(3a-b-5)2=0
∴
解这个方程组,得
∴(3a+2b)2020= (-1)2020 =1
根据“若几个非负数的和等于0,则这几个非负数都为0”得到关于a、b的方程组,然后解方程组即可.
延伸拓展
2.已知 x,y 满足方程组
求 x2+4y2的值.
把③代入④,得 ,
解:由①,得 3(x2+4y2)=47+2xy,即 .③
由②,得 2(x2+4y2)=36-xy.④
解得 xy=2,
把 xy=2 代入③,得 x2+4y2=17.
延伸拓展
课堂小结
05
用代入消元法解二元一次方程组的步骤:
1.变形
选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数.
把 y=ax+b (或 x=ay+b) 代入另一个没有变形的方程.
2.代入
3.求解
解消元后的一元一次方程.
4.回代
把求得的未知数的值代入步骤1中变形后的方程.
5.写解
把两个未知数的值用大括号联立起来.
课堂小结
课堂小结
三类代入消元法
(1)直接代入:方程组中含有用一个未知数表示另一个未知数的形式的方程;
(2)变形代入:方程组中含有未知数的系数为1或-1的方程;
(3)整体代入:方程组中某一未知数的系数成倍数关系.
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
代入法
人教版数学 七年级下册
学习目标
01
学习目标
会用代入消元法解简单的二元一次方程组。
理解解二元一次方程组的思路是“消元”, 经历从未知向已知转化的过程,体会化归思想。
新课教学
02
含有两个未知数,并且含有未知数的项的次数都是 1 的方程
什么叫做二元一次方程?
有两个未知数,含有每个未知数的项的次数都是 1,并且一共有两个方程的方程组
什么叫做二元一次方程组?
知识回顾
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
知识回顾
上节课我们学习了二元一次方程组和二元一次方程组的解,那给出一个一般的二元一次方程组,我们怎么得到它的解呢?本节课我们将学习解二元一次方程组的方法.
新课引入
知识点:用代入法解二元一次方程组
解:设胜 x 场,负 y 场.
则
篮球联赛中,每场都要分出胜负,每队胜 1 场得 2 分,负 1 场得 1 分. 某队 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
你能根据问题中的等量关系列出二元一次方程组吗?
新知讲解
解:设胜 x 场,则负 (10-x) 场.
则 2x+(10-x)=16.
这个实际问题能列一元一次方程求解吗?
篮球联赛中,每场都要分出胜负,每队胜 1 场得 2 分,负 1 场得 1 分. 某队 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
新知讲解
对比方程和方程组,你能发现它们之间的关系吗?
2x+(10-x)=16.
y=10-x
将未知数的个数由多化少、逐一解决的思想,叫做消元思想.
x=6
y=4
新知讲解
解二元一次方程组的基本思路:“消元”
二元一次方程组
一元一次方程
消元
转化
把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做代入消元法,简称代入法.
新知讲解
对于二元一次方程组
代入①或代入②可不可以?哪种运算更简便?
解:由①,得 y=10-x,③
把③代入②,得 2x+10-x=16,
解这个方程得 x=6.
①
②
把 x=6 代入③,得 y=4.
这个方程组的解是
答:这个队胜 6 场、负 4 场.
2.怎样求出 y ?
1.你能写出求 x 的过程吗?
新知讲解
用代入消元法解二元一次方程组的步骤:
1.变形
选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数.
把 y=ax+b (或 x=ay+b) 代入另一个没有变形的方程.
2.代入
3.求解
解消元后的一元一次方程.
4.回代
把求得的未知数的值代入步骤1中变形后的方程.
5.写解
把两个未知数的值用大括号联立起来.
新知讲解
三类代入消元法
(1)直接代入:方程组中含有用一个未知数表示另一个未知数的形式的方程;
(2)变形代入:方程组中含有未知数的系数为1或-1的方程;
(3)整体代入:方程组中某一未知数的系数成倍数关系.
新知讲解
例1 用代入法解方程组
变形
代入
求解
回代
写解
①
②
所以这个方程组的解是
把 y=-1代入③,得 x=2.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x=y+3 .③
解这个方程,得 y=-1.
新知讲解
例1 用代入法解方程组
变形
代入
求解
回代
写解
①
②
所以这个方程组的解是
把 y=-1代入③,得 x=2.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x=y+3 .③
解这个方程,得 y=-1.
新知讲解
例1 用代入法解方程组
变形
代入
求解
回代
写解
①
②
所以这个方程组的解是
把 y=-1代入③,得 x=2.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x=y+3 .③
解这个方程,得 y=-1.
新知讲解
二
元
一
次
方
程
组
x-y=3
3x-8y=14
y=-1
x = 2
解得 y
变形
解得 x
消去 x
一元一次方程
3(y+3)-8y=14
x =y+3
用y+3代替x,消未知数x.
用代入法解方程组:
代入
新知讲解
小试牛刀
03
1.用代入法解方程组 时,代入正确的是( )
A. x-2-x=4
B. x-2-2x=4
C. x-2+2x=4
D. x-2+x=4
x-2(1-x)=4
x-2+2x=4
C
小试牛刀
2.解方程组
①
②
所以这个方程组的解是
把 x=1 代入③,得 y=3-2=1.
把③代入②,得 9x+8(3x-2)=17.
解:由①,得 y=3x-2. ③
解这个方程,得 x=1.
小试牛刀
3.解方程组
①
②
所以这个方程组的解是
把 y=2 代入③,得 .
把③代入②,得 .
解:由①,得 .③
解这个方程,得 y=2.
小试牛刀
4.解方程组
解得 x=3.
把 y=2 代入③,得 2x=16-5×2=6.
把③代入②,得 4(16-5y)-7y=10.
解:由①,得 2x=16-5y. ③
解这个方程,得 y=2.
①
②
所以这个方程组的解是
小试牛刀
5.解方程组
把 x=2 代入①,得 y=1.
解:把①代入②,得 5x-3×3=1.
解这个方程,得 x=2.
①
②
所以这个方程组的解是
小试牛刀
延伸拓展
04
1.已知 |a+2b+3|+(3a-b-5)2=0,则(3a+2b)2020=___.
1
解析:∵|a+2b+3|≥0,(3a-b-5)2 ≥0, |a+2b+3|+(3a-b-5)2=0
∴
解这个方程组,得
∴(3a+2b)2020= (-1)2020 =1
根据“若几个非负数的和等于0,则这几个非负数都为0”得到关于a、b的方程组,然后解方程组即可.
延伸拓展
2.已知 x,y 满足方程组
求 x2+4y2的值.
把③代入④,得 ,
解:由①,得 3(x2+4y2)=47+2xy,即 .③
由②,得 2(x2+4y2)=36-xy.④
解得 xy=2,
把 xy=2 代入③,得 x2+4y2=17.
延伸拓展
课堂小结
05
用代入消元法解二元一次方程组的步骤:
1.变形
选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数.
把 y=ax+b (或 x=ay+b) 代入另一个没有变形的方程.
2.代入
3.求解
解消元后的一元一次方程.
4.回代
把求得的未知数的值代入步骤1中变形后的方程.
5.写解
把两个未知数的值用大括号联立起来.
课堂小结
课堂小结
三类代入消元法
(1)直接代入:方程组中含有用一个未知数表示另一个未知数的形式的方程;
(2)变形代入:方程组中含有未知数的系数为1或-1的方程;
(3)整体代入:方程组中某一未知数的系数成倍数关系.
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
