9.1.1《不等式及其解集》(1) 课件(共34张PPT)
文档属性
| 名称 | 9.1.1《不等式及其解集》(1) 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 09:45:30 | ||
图片预览











文档简介
(共34张PPT)
不等式及其解集
人教版数学 七年级下册
学习目标
01
学习目标
了解不等式及其解的概念。
学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想。
理解不等式的解集及解不等式的意义。
新课教学
02
如图所示,处于平衡状态的托盘天平的右盘放上一质量为 50 g 的砝码,左盘放上一个圆球后向左倾斜,问圆球的质量 x g 与质量为 50 g 的砝码之间具有怎样的关系?
x g
50 g
我们很容易知道圆球的质量大于砝码的质量,即 x > 50.
新课引入
知识点1:不等式的概念
某商场推出了购物领红包活动.顾客购物满 100 元即可获得 1 个现金红包,红包金额随机,高于 1 元,且低于 100 元.你能用关系式表示可获红包金额 x 的大小吗?
x>1 且 x<100
新课引入
一辆匀速行驶的汽车在 11 : 20 距离 A 地 50 千米,要在 12 : 00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从时间上看,汽车要在 12 : 00 之前驶过 A 地,
则以这个速度行驶 50 km 所用的时间不到 h,即. ①
新课引入
一辆匀速行驶的汽车在 11 :20 距离 A 地 50 千米,要在 12 :00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从路程上看,汽车要在 12 : 00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即. ②式子①和②从不同角度表示了车速应满足的条件.
新课引入
观察以上得到的关系式:
x>50 x>1 且 x<100
左右不相等.
它们有什么共同的特点?
一般地,用不等号表示大小关系的式子叫做不等式.
新知讲解
常见的不等号:
符号 名称 读法 实际意义 举例
< 小于号 小于 小于、不足 -2<3
> 大于号 大于 大于、超出 3>1
≤ 小于等于号 小于或等于 不大于、不超过、至多 x≤3
≥ 大于等于号 大于或等于 不小于、不低于、至少 x≥-6
≠ 不等号 不等于 不相等 3≠4
新知讲解
有些不等式中不含未知数,如 3<4;有些不等式中含有未知数,如 2x<1.对于含有未知数的不等式,当未知数取某些值时,不等式的左、右两边符合不等号所表示的大小关系,我们就说不等式成立;否则,不等式不成立.
不等号具有方向性,不等号两边的数不能随意交换.
新知讲解
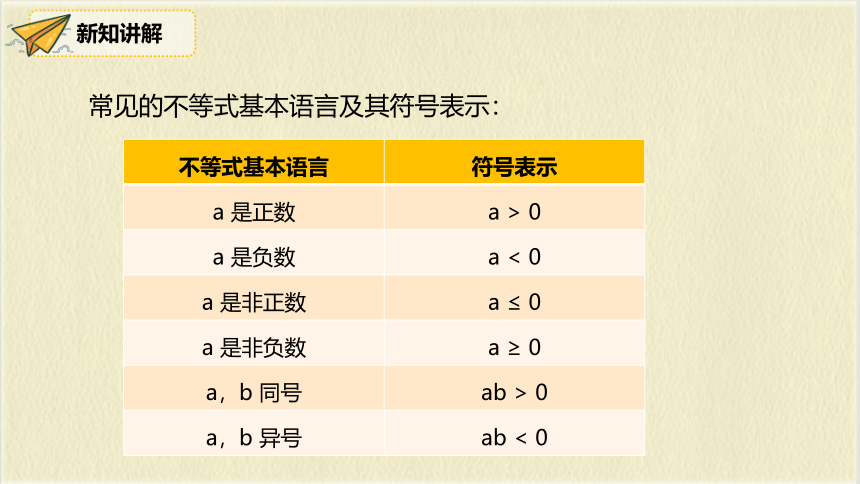
常见的不等式基本语言及其符号表示:
不等式基本语言 符号表示
a 是正数 a > 0
a 是负数 a < 0
a 是非正数 a ≤ 0
a 是非负数 a ≥ 0
a,b 同号 ab > 0
a,b 异号 ab < 0
新知讲解
下列式子中是不等式的有_________.(填序号)
① 3<2;
② 2x2-3>0;
③ 5y2-8;
④ 2x+3=7;
⑤ 3x+1≤7;
⑥ x≠5.
不含不等号
含等号
①②⑤⑥
新知讲解
知识点2:不等式的解与解集
下面给出的数,能使不等式 x>50 成立吗?
20, 50, 100.
当x=20时,20<50,不成立.
当x=50时,50=50,不成立.
当x=100时,100>50, 成立.
新知讲解
使不等式成立的未知数的值叫做不等式的解.
一般情况下,不等式的解有无数个,但不等式的特殊解可以是有限个.
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
新知讲解
判断下列数中哪些是不等式 的解:60,73,74.9,75.1,76,79,80,90.
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
新知讲解
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
你从表格中发现了什么规律?
比 75 小的数都不是不等式的解,比 75 大的数都是不等式的解.
新知讲解
小试牛刀
03
1.在 -2,-2.5,0,1 中,是不等式 2x>1 的解的是______.
2×(-2)=-4<1
2×0=0<1
2×(-2.5)=-5<1
1
小试牛刀
2.下列说法中,正确的是( )
A. -3 是不等式 x+4<1 的解
B. x>1 是不等式 x+1>0 的解集
C. 不等式 x≥-3 的负整数解有无数个
D. 不等式 x<5 的非正整数解有无数个
-3+4=1
0+1>0,但0<1
-3,-2,-1
D
小试牛刀
不含不等号
含等号
含等号
小试牛刀
C
3.有下列数学表达式:
① -0.0001<0 ② m-3n>1
③ 2x-3 =0 ④ y=x+2
⑤ d≠-1 ⑥ x-xy+(-y)
其中是不等式的有( )
A. 1个 B. 2个 C. 3个 D. 4个
4.在数 -4,-1,0,3,10 中,是不等式 x-2<3 的解的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
-4-2=-6<3
0-2=-2<3
10-2=8>3
-1-2=-3<3
3-2=1<3
C
小试牛刀
5.用不等式表示:
(1) x 的 2 倍与 5 的差不大于 1;
(2) x 的 与 x 的 的和是非负数;
(3) a 与 3 的和不小于 5;
(4) a 的 20% 与 a 的和大于 a 的 3 倍.
2x-5≤1
a+3≥5
20%a+a>3a
小试牛刀
延伸拓展
04
1.据某天气网站预测,某市最高气温是 6°C,最低气温是 -1 °C,则当天该市气温 t (单位:°C)的变化范围是( )
A. t > 6
B. t < l
C. -1 < t < 6
D. -1 ≤ t ≤ 6
t ≤ 6
t ≥ -1
D
延伸拓展
2.用不等式表示:
(1) a 的 与 1 的和小于-3;
(2) x 与 3 的差不大于 6;
(3) 8 与 x 的差的 是非负数.
x-3≤6
延伸拓展
2.一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
A. x > -1 B. x ≥ - 1
C. x < -1 D. x ≤ -1
向右 > 或 ≥
空心 >
A
延伸拓展
课堂小结
05
求不等式的解集的过程叫做解不等式.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
用不等号表示大小关系的式子
不等式
概念
使不等式成立的未知数的值
解
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集
解集
课堂小结
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别
联系
解集包含所有的解,所有的解组成解集
能使不等式成立的未知数的值
能使不等式成立的所有未知数的值
课堂小结
怎样表示不等式的解集呢?
用式子:
用最简形式的不等式(如 x>a 或 x用数轴:
一般标出数轴上某一区间,其中的点对应的数值都是不等式的解.
课堂小结
不等式的解集 x > a x < a x ≥ a x ≤ a
数轴表示
用数轴表示不等式的解集的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点).
2.定方向:大于向右,小于向左.
0
a
0
a
0
a
0
a
常见不等式的解集在数轴上的表示:
课堂小结
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
不等式及其解集
人教版数学 七年级下册
学习目标
01
学习目标
了解不等式及其解的概念。
学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想。
理解不等式的解集及解不等式的意义。
新课教学
02
如图所示,处于平衡状态的托盘天平的右盘放上一质量为 50 g 的砝码,左盘放上一个圆球后向左倾斜,问圆球的质量 x g 与质量为 50 g 的砝码之间具有怎样的关系?
x g
50 g
我们很容易知道圆球的质量大于砝码的质量,即 x > 50.
新课引入
知识点1:不等式的概念
某商场推出了购物领红包活动.顾客购物满 100 元即可获得 1 个现金红包,红包金额随机,高于 1 元,且低于 100 元.你能用关系式表示可获红包金额 x 的大小吗?
x>1 且 x<100
新课引入
一辆匀速行驶的汽车在 11 : 20 距离 A 地 50 千米,要在 12 : 00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从时间上看,汽车要在 12 : 00 之前驶过 A 地,
则以这个速度行驶 50 km 所用的时间不到 h,即. ①
新课引入
一辆匀速行驶的汽车在 11 :20 距离 A 地 50 千米,要在 12 :00 之前驶过 A 地,车速应满足什么条件?
分析:设车速是 x km/h.
从路程上看,汽车要在 12 : 00 之前驶过 A 地,则以这个速度行驶 h 的路程要超过 50 km,即. ②式子①和②从不同角度表示了车速应满足的条件.
新课引入
观察以上得到的关系式:
x>50 x>1 且 x<100
左右不相等.
它们有什么共同的特点?
一般地,用不等号表示大小关系的式子叫做不等式.
新知讲解
常见的不等号:
符号 名称 读法 实际意义 举例
< 小于号 小于 小于、不足 -2<3
> 大于号 大于 大于、超出 3>1
≤ 小于等于号 小于或等于 不大于、不超过、至多 x≤3
≥ 大于等于号 大于或等于 不小于、不低于、至少 x≥-6
≠ 不等号 不等于 不相等 3≠4
新知讲解
有些不等式中不含未知数,如 3<4;有些不等式中含有未知数,如 2x<1.对于含有未知数的不等式,当未知数取某些值时,不等式的左、右两边符合不等号所表示的大小关系,我们就说不等式成立;否则,不等式不成立.
不等号具有方向性,不等号两边的数不能随意交换.
新知讲解
常见的不等式基本语言及其符号表示:
不等式基本语言 符号表示
a 是正数 a > 0
a 是负数 a < 0
a 是非正数 a ≤ 0
a 是非负数 a ≥ 0
a,b 同号 ab > 0
a,b 异号 ab < 0
新知讲解
下列式子中是不等式的有_________.(填序号)
① 3<2;
② 2x2-3>0;
③ 5y2-8;
④ 2x+3=7;
⑤ 3x+1≤7;
⑥ x≠5.
不含不等号
含等号
①②⑤⑥
新知讲解
知识点2:不等式的解与解集
下面给出的数,能使不等式 x>50 成立吗?
20, 50, 100.
当x=20时,20<50,不成立.
当x=50时,50=50,不成立.
当x=100时,100>50, 成立.
新知讲解
使不等式成立的未知数的值叫做不等式的解.
一般情况下,不等式的解有无数个,但不等式的特殊解可以是有限个.
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
新知讲解
判断下列数中哪些是不等式 的解:60,73,74.9,75.1,76,79,80,90.
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
新知讲解
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
你从表格中发现了什么规律?
比 75 小的数都不是不等式的解,比 75 大的数都是不等式的解.
新知讲解
小试牛刀
03
1.在 -2,-2.5,0,1 中,是不等式 2x>1 的解的是______.
2×(-2)=-4<1
2×0=0<1
2×(-2.5)=-5<1
1
小试牛刀
2.下列说法中,正确的是( )
A. -3 是不等式 x+4<1 的解
B. x>1 是不等式 x+1>0 的解集
C. 不等式 x≥-3 的负整数解有无数个
D. 不等式 x<5 的非正整数解有无数个
-3+4=1
0+1>0,但0<1
-3,-2,-1
D
小试牛刀
不含不等号
含等号
含等号
小试牛刀
C
3.有下列数学表达式:
① -0.0001<0 ② m-3n>1
③ 2x-3 =0 ④ y=x+2
⑤ d≠-1 ⑥ x-xy+(-y)
其中是不等式的有( )
A. 1个 B. 2个 C. 3个 D. 4个
4.在数 -4,-1,0,3,10 中,是不等式 x-2<3 的解的个数为( )
A. 2个 B. 3个 C. 4个 D. 5个
-4-2=-6<3
0-2=-2<3
10-2=8>3
-1-2=-3<3
3-2=1<3
C
小试牛刀
5.用不等式表示:
(1) x 的 2 倍与 5 的差不大于 1;
(2) x 的 与 x 的 的和是非负数;
(3) a 与 3 的和不小于 5;
(4) a 的 20% 与 a 的和大于 a 的 3 倍.
2x-5≤1
a+3≥5
20%a+a>3a
小试牛刀
延伸拓展
04
1.据某天气网站预测,某市最高气温是 6°C,最低气温是 -1 °C,则当天该市气温 t (单位:°C)的变化范围是( )
A. t > 6
B. t < l
C. -1 < t < 6
D. -1 ≤ t ≤ 6
t ≤ 6
t ≥ -1
D
延伸拓展
2.用不等式表示:
(1) a 的 与 1 的和小于-3;
(2) x 与 3 的差不大于 6;
(3) 8 与 x 的差的 是非负数.
x-3≤6
延伸拓展
2.一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
A. x > -1 B. x ≥ - 1
C. x < -1 D. x ≤ -1
向右 > 或 ≥
空心 >
A
延伸拓展
课堂小结
05
求不等式的解集的过程叫做解不等式.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
用不等号表示大小关系的式子
不等式
概念
使不等式成立的未知数的值
解
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集
解集
课堂小结
不等式的解与不等式的解集的区别与联系
不等式的解 不等式的解集
区别
联系
解集包含所有的解,所有的解组成解集
能使不等式成立的未知数的值
能使不等式成立的所有未知数的值
课堂小结
怎样表示不等式的解集呢?
用式子:
用最简形式的不等式(如 x>a 或 x
一般标出数轴上某一区间,其中的点对应的数值都是不等式的解.
课堂小结
不等式的解集 x > a x < a x ≥ a x ≤ a
数轴表示
用数轴表示不等式的解集的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点).
2.定方向:大于向右,小于向左.
0
a
0
a
0
a
0
a
常见不等式的解集在数轴上的表示:
课堂小结
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
