6.1.2《用计算器求算术平方根及其大小比较》课件(共32张PPT)
文档属性
| 名称 | 6.1.2《用计算器求算术平方根及其大小比较》课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 11:58:37 | ||
图片预览










文档简介
(共32张PPT)
用计算器求算术平方根及其大小比较
人教版数学 七年级下册
学习目标
01
学习目标
会用计算器求算术平方根。
掌握算术平方根的估算及大小比较。
新课教学
02
填空:
(1) 一个数的算术平方根是3,则这个数是 ;
(2) 一个自然数的算术平方根为a,则这个自然数是___;和这个自然数相邻的下一个自然数是 ;
(3) 的算术平方根为 ;
(4) 2 的算术平方根为____.
3
9
a2
a2+1
知识回顾
通过上节课的学习我们知道 的算术平方根是 3 ,
2 的算术平方根是 ,那么 有多大呢?
新课引入
能否用两个面积为 1 dm2 的小正方形拼成一个面积为 2 dm2 的大正方形?
知识点1:算术平方根的估算及大小比较
新课讲解
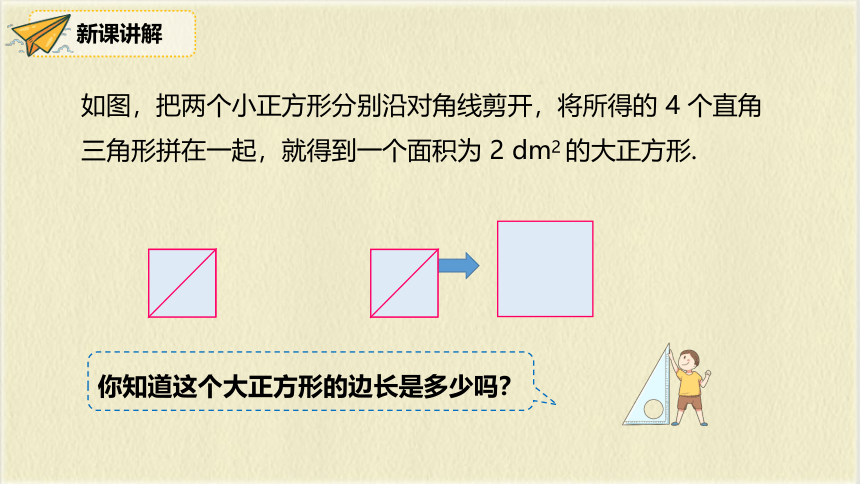
如图,把两个小正方形分别沿对角线剪开,将所得的 4 个直角三角形拼在一起,就得到一个面积为 2 dm2 的大正方形.
你知道这个大正方形的边长是多少吗?
新课讲解
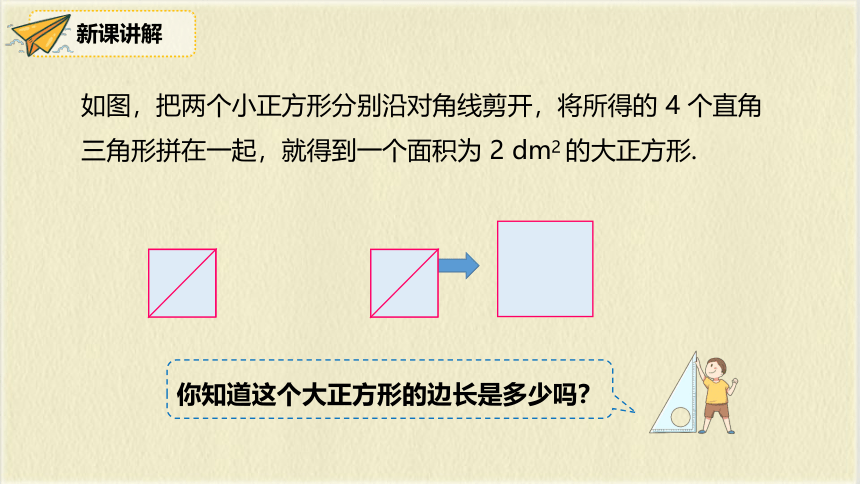
如图,把两个小正方形分别沿对角线剪开,将所得的 4 个直角三角形拼在一起,就得到一个面积为 2 dm2 的大正方形.
你知道这个大正方形的边长是多少吗?
新课讲解
设大正方形的边长为 x dm,则
x2 = 2
由算术平方根的意义可知
x =
所以大正方形的边长是 dm
小正方形的对角线的长是多少呢?
小正方形的对角线的长即为大正方形的边长
新课讲解
因为 12=1,22=4,
而 1 < 2 < 4 ,
所以 1 < < 2.
探究: 有多大呢?
对算术平方根进行估算时,通常利用与被开方数比较接近的两个完全平方数的算术平方根来估计这个被开方数的算术平方根的大小.
新课讲解
因为1.42 = 1.96,1.52 = 2.25,而 1.96 < 2 < 2.25,
所以 1.4 < < 1.5;
能不能得到更精确的范围?
因为1.412 = 1.9881,1.422 = 2.0164,而 1.9881 < 2 < 2.0164,
所以 1.41 < < 1.42;
因为1.4142 = 1.999396,1.4152 = 2.002225,
而 1.999396 < 2 < 2.002225,所以 1.414 < < 1.415;
小试牛刀
如此进行下去,可以得到 更精确的近似值. 事实上 =1.414213562373…,它是一个无限不循环小数.
小数位数无限,且小数部分不循环的小数称为无限不循环小数.
新课讲解
(1)确定 的整数部分:根据算术平方根的定义,若 夹在两个连续正整数 m,n (m(2)确定 的小数部分:从较小整数 m 开始,逐步加 0.1,并求其平方,采用与(1)类似的方法确定 的十分位上的数;再用同样的方法确定其他数位上的数,直到能按照精确度估计近似值为止(若要求精确到百分位,估算过程中需计算到千分位,再用四舍五入法确定百分位的值).
夹逼法按照精确度估计 的近似值
新课讲解
小试牛刀
03
1.小丽想用一块面积为 400 cm2 的正方形纸片,沿着边的方向裁出一块面积为 300 cm2 的长方形纸片,使它的长宽之比为 3 : 2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
小试牛刀
解:设长方形纸片的长为 3x cm ,宽为 2x cm,
根据边长与面积的关系得
3x 2x = 300 ,
6x2 = 300 ,
x2 = 50,
x = ,
因此长方形纸片的长为 3 cm .
小试牛刀
因为 50 > 49,所以 > 7.
由上可知 3 > 21,则长方形纸片的长应该大于 21 cm.
因为 = 20,所以正方形纸片的边长只有 20 cm.
这样,长方形纸片的长将大于正方形纸片的边长.
答:不能同意小明的说法. 小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
小试牛刀
2.估算 的近似值(精确到0.01).
解:∵ 22=4,32=9,∴ 2< <3.
∵ 2.22 =4.84,2.32 =5.29,∴ 2.2< <2.3,
∵ 2.232 =4. 9729,2.242 =5. 0176,∴ 2.23 < <2.24.
∵ 2.2362 =4.999696,2.2372 =5.004169,∴ 2.236< <2.237,
∴ ≈2.24.
确定整数部分为 2
确定十分位为 2
四舍五入确定百分位为 4
小试牛刀
知识点2:用计算器求正有理数的算术平方根
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数 a 的算术平方根(或其近似数).
a
=
按键顺序:
计算器的型号不同,按键顺序可能有所不同,要注意阅读使用说明书.
拓展探究
… …
… …
(1)利用计算器计算下表中的算术平方根,并将计算结果填在表中.
0.25
0.791
2.5
7.91
25
79.1
250
你发现了什么规律?
拓展探究
(2)用计算器计算 (精确到0.001),并利用你在(1)中发现的规律说出 , , 的近似值,你能根据 的值说出 是多少吗?
用计算器可得 ,根据(1)中发现的规律可知 , , ;
根据 的值不能说出 是多少.
拓展探究
被开方数的小数点向右每移动 位,它的算术平方根的小数点就向右移动 位;
被开方数的小数点向左每移动 位,它的算术平方根的小数点就向左移动 位.
2
1
2
1
… …
… …
0.25
0.791
2.5
7.91
25
79.1
250
3. 用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
解:(1)依次按键 ,
显示:56.
∴ .
(2)依次按键 ,
显示:1.414213562.
∴ .
=
3136
=
2
小试牛刀
4.用计算器求下列各式的值:
(1) ; (2) (精确到0.01).
解:(1)依次按键 ,
显示:85.
所以 = 85.
(2)依次按键 ,
显示:3.464101615.
所以 ≈3.46.
7
5
2
2
=
1
2
=
小试牛刀
7
5
2
2
=
1
2
=
5.估算 的值 ( )
A.在 1 和 2 之间 B.在 2 和 3 之间
C.在 3 和 4 之间 D.在 4 和 5 之间
解析:因为 42<19<52,
所以 4< <5,
所以 2< <3.
B
小试牛刀
6.比较下列各组数的大小:
(1) 与 5; (2) 与 .
解:(1)∵ 26>25,
∴ > ,
即 >5.
(2) ∵ 12<2<22,
∴ 1< <2,
∴ 0< -1<1,
∴ .
小试牛刀
7.通过估算比较下列各组数的大小:
(1) 与1.9; (2) 与1.5.
解:(1)因为 5>4,
所以 >2,
所以 >1.9.
(2)因为 6>4,
所以 > 2,
所以 >
所以 >1.5.
小试牛刀
解析: ∵ < <,
∴ 6< < 7,
∵ 6.52=42.25,
∴ 6< <6.5,
∴ ≈6.
8.估算: ≈ (结果精确到 1).
6
小试牛刀
课堂小结
04
比较大小
算术平方根的求值
估算
用计算器计算
课堂小结
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
用计算器求算术平方根及其大小比较
人教版数学 七年级下册
学习目标
01
学习目标
会用计算器求算术平方根。
掌握算术平方根的估算及大小比较。
新课教学
02
填空:
(1) 一个数的算术平方根是3,则这个数是 ;
(2) 一个自然数的算术平方根为a,则这个自然数是___;和这个自然数相邻的下一个自然数是 ;
(3) 的算术平方根为 ;
(4) 2 的算术平方根为____.
3
9
a2
a2+1
知识回顾
通过上节课的学习我们知道 的算术平方根是 3 ,
2 的算术平方根是 ,那么 有多大呢?
新课引入
能否用两个面积为 1 dm2 的小正方形拼成一个面积为 2 dm2 的大正方形?
知识点1:算术平方根的估算及大小比较
新课讲解
如图,把两个小正方形分别沿对角线剪开,将所得的 4 个直角三角形拼在一起,就得到一个面积为 2 dm2 的大正方形.
你知道这个大正方形的边长是多少吗?
新课讲解
如图,把两个小正方形分别沿对角线剪开,将所得的 4 个直角三角形拼在一起,就得到一个面积为 2 dm2 的大正方形.
你知道这个大正方形的边长是多少吗?
新课讲解
设大正方形的边长为 x dm,则
x2 = 2
由算术平方根的意义可知
x =
所以大正方形的边长是 dm
小正方形的对角线的长是多少呢?
小正方形的对角线的长即为大正方形的边长
新课讲解
因为 12=1,22=4,
而 1 < 2 < 4 ,
所以 1 < < 2.
探究: 有多大呢?
对算术平方根进行估算时,通常利用与被开方数比较接近的两个完全平方数的算术平方根来估计这个被开方数的算术平方根的大小.
新课讲解
因为1.42 = 1.96,1.52 = 2.25,而 1.96 < 2 < 2.25,
所以 1.4 < < 1.5;
能不能得到更精确的范围?
因为1.412 = 1.9881,1.422 = 2.0164,而 1.9881 < 2 < 2.0164,
所以 1.41 < < 1.42;
因为1.4142 = 1.999396,1.4152 = 2.002225,
而 1.999396 < 2 < 2.002225,所以 1.414 < < 1.415;
小试牛刀
如此进行下去,可以得到 更精确的近似值. 事实上 =1.414213562373…,它是一个无限不循环小数.
小数位数无限,且小数部分不循环的小数称为无限不循环小数.
新课讲解
(1)确定 的整数部分:根据算术平方根的定义,若 夹在两个连续正整数 m,n (m
夹逼法按照精确度估计 的近似值
新课讲解
小试牛刀
03
1.小丽想用一块面积为 400 cm2 的正方形纸片,沿着边的方向裁出一块面积为 300 cm2 的长方形纸片,使它的长宽之比为 3 : 2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
小试牛刀
解:设长方形纸片的长为 3x cm ,宽为 2x cm,
根据边长与面积的关系得
3x 2x = 300 ,
6x2 = 300 ,
x2 = 50,
x = ,
因此长方形纸片的长为 3 cm .
小试牛刀
因为 50 > 49,所以 > 7.
由上可知 3 > 21,则长方形纸片的长应该大于 21 cm.
因为 = 20,所以正方形纸片的边长只有 20 cm.
这样,长方形纸片的长将大于正方形纸片的边长.
答:不能同意小明的说法. 小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
小试牛刀
2.估算 的近似值(精确到0.01).
解:∵ 22=4,32=9,∴ 2< <3.
∵ 2.22 =4.84,2.32 =5.29,∴ 2.2< <2.3,
∵ 2.232 =4. 9729,2.242 =5. 0176,∴ 2.23 < <2.24.
∵ 2.2362 =4.999696,2.2372 =5.004169,∴ 2.236< <2.237,
∴ ≈2.24.
确定整数部分为 2
确定十分位为 2
四舍五入确定百分位为 4
小试牛刀
知识点2:用计算器求正有理数的算术平方根
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数 a 的算术平方根(或其近似数).
a
=
按键顺序:
计算器的型号不同,按键顺序可能有所不同,要注意阅读使用说明书.
拓展探究
… …
… …
(1)利用计算器计算下表中的算术平方根,并将计算结果填在表中.
0.25
0.791
2.5
7.91
25
79.1
250
你发现了什么规律?
拓展探究
(2)用计算器计算 (精确到0.001),并利用你在(1)中发现的规律说出 , , 的近似值,你能根据 的值说出 是多少吗?
用计算器可得 ,根据(1)中发现的规律可知 , , ;
根据 的值不能说出 是多少.
拓展探究
被开方数的小数点向右每移动 位,它的算术平方根的小数点就向右移动 位;
被开方数的小数点向左每移动 位,它的算术平方根的小数点就向左移动 位.
2
1
2
1
… …
… …
0.25
0.791
2.5
7.91
25
79.1
250
3. 用计算器求下列各式的值:
(1) ; (2) (精确到0.001).
解:(1)依次按键 ,
显示:56.
∴ .
(2)依次按键 ,
显示:1.414213562.
∴ .
=
3136
=
2
小试牛刀
4.用计算器求下列各式的值:
(1) ; (2) (精确到0.01).
解:(1)依次按键 ,
显示:85.
所以 = 85.
(2)依次按键 ,
显示:3.464101615.
所以 ≈3.46.
7
5
2
2
=
1
2
=
小试牛刀
7
5
2
2
=
1
2
=
5.估算 的值 ( )
A.在 1 和 2 之间 B.在 2 和 3 之间
C.在 3 和 4 之间 D.在 4 和 5 之间
解析:因为 42<19<52,
所以 4< <5,
所以 2< <3.
B
小试牛刀
6.比较下列各组数的大小:
(1) 与 5; (2) 与 .
解:(1)∵ 26>25,
∴ > ,
即 >5.
(2) ∵ 12<2<22,
∴ 1< <2,
∴ 0< -1<1,
∴ .
小试牛刀
7.通过估算比较下列各组数的大小:
(1) 与1.9; (2) 与1.5.
解:(1)因为 5>4,
所以 >2,
所以 >1.9.
(2)因为 6>4,
所以 > 2,
所以 >
所以 >1.5.
小试牛刀
解析: ∵ < <,
∴ 6< < 7,
∵ 6.52=42.25,
∴ 6< <6.5,
∴ ≈6.
8.估算: ≈ (结果精确到 1).
6
小试牛刀
课堂小结
04
比较大小
算术平方根的求值
估算
用计算器计算
课堂小结
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
