6.3.1《实数》课件(共28张PPT)
文档属性
| 名称 | 6.3.1《实数》课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 11:58:37 | ||
图片预览






文档简介
(共28张PPT)
实 数
人教版数学 七年级下册
学习目标
01
学习目标
理解无理数和实数的概念。
对实数进行分类,判断一个数是有理数还是无理数。
理解实数和数轴上的点一一对应。
新课教学
02
有理数知识点回顾
按整数和分数的关系分类:
按正数、负数、和零的关系分类:
知识回顾
上面的分数都可以写成有限小数或无限循环小数形式。
而任何一个有理数都可以写成有限小数或无限循环小数形式,
反之,有限小数和无限循环小数是有理数。
将下列分数写成小数的形式,你有什么发现?
,-
=0.75 ,-
=1.2
= 0.81818181… =0.81
新课引入
无理数
无限不循环的小数叫做无理数。
结合本章所学知识,举例:
无理数的分类:
结合无理数概念,举例:
.333133343…,3.3456789…,…
1.圆周率π及一些含π的数是无理数。
2.含根号的数不一定是无理数。(例: 等)
【注意】
新知讲解
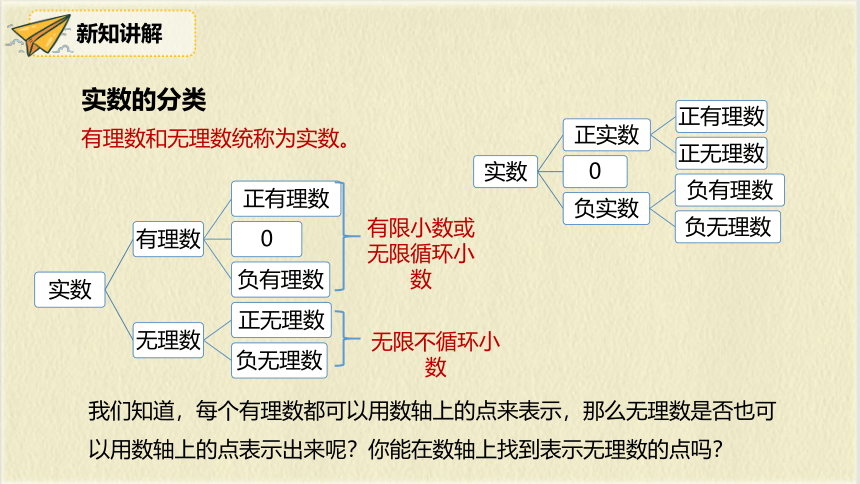
实数的分类
有理数和无理数统称为实数。
有限小数或无限循环小数
无限不循环小数
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示无理数的点吗?
新知讲解
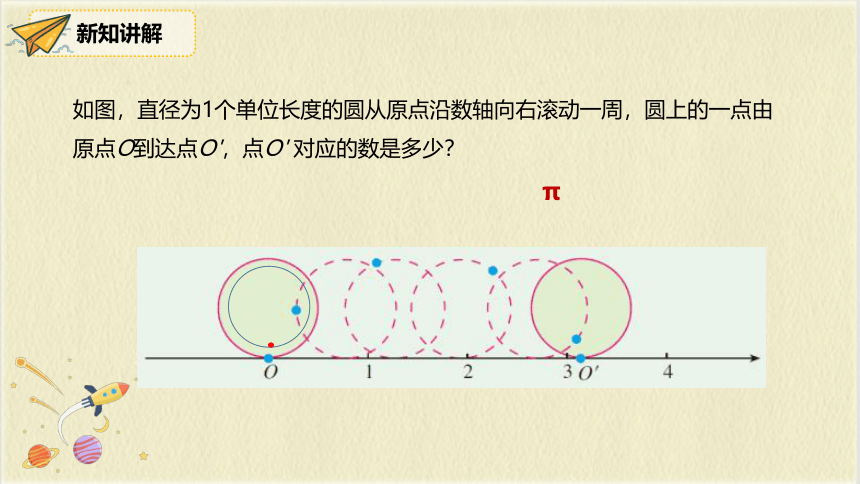
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点O到达点O',点O' 对应的数是多少?
π
新知讲解
数轴上的点可以表示有理数,那它可以表示无理数吗,你能在数轴上画出表示的点吗?
0
1
2
3
4
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数。
新知讲解
小试牛刀
03
1.在实数中,无理数的个数为( )。
A.1个 B.2个 C.3个 D.4个
小试牛刀
B
2.下列说法不正确的是( ).
A.如果数轴上的点表示的数不是有理数,那么就一定是无理数
B.大小介于两个有理数之间的无理数有无数个
C.-1的立方是-1,立方根也是-1
D.两个实数,较大者的平方也较大
D
小试牛刀
3.如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心、正方形对角线的长为半径画弧,交数轴于点A,则点A表示的数是( ).
A.- B.2- C.1- D.1+
小试牛刀
B
4.下列说法正确的有( )
①数轴上任意一点都表示一个有理数;
②任意一个无理数都可以用数轴上的一个点来表示;
③任意一个实数都可以用数轴上的一个点来表示;
④有理数与数轴上的点一 一对应.
实数
实数
B
A.1个 B.2个 C.3 D.4个
小试牛刀
5.如图,数轴上A,B,C,D四点中,与-对应的点距离最近的是( ).
A.点A B.点B C.点C D.点D
小试牛刀
B
6.比较 与 的大小.
解:
∵2<4,
∴,即<2,
∴<0,
∴<0,
< .
小试牛刀
延伸拓展
04
1.把下列各数填在相应的大括号内.
.
非负整数:{ …};
整数:{ …};
负分数:{ …};
延伸拓展
1.把下列各数填在相应的大括号内.
正实数:{ …};
有理数:{ …};
无理数:{ …}.
.
延伸拓展
2.比较3,,的大小( )
A. 3<< B. 3<<
C. <3< D. <<3
3=<
3=>
C
延伸拓展
课堂小结
05
无限不循环小数
实数
无理数
实数的分类
实数与数轴上点的关系
实数的大小比较
课堂小结
(1)对实数进行分类时,某些数应先进行计算或化简,然后根据最后结果进行分类,不能看到带根号的数,就认为是无理数,不能看到有分数线的数,就认为是有理数. (2)在实数范围内,一个数不是有理数,那么它一定是无理数,反之亦成立.
课堂小结
(1)按定义分:
你能给实数分类吗?
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
课堂小结
(2)按大小分:
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
实数的分类有不同的方法,但不论用哪一种分类方法,都要做到不重不漏.
课堂小结
无理数与有理数的区别
(1)任何有理数都能化成分数(整数可以看成分母是1的分数),无理数不能化成分数.
(2)任何一个有理数都可以化成有限小数(把整数看成小数点后是0的小数)或无限循环小数,无理数是无限不循环小数.
课堂小结
谢谢观看!
实 数
人教版数学 七年级下册
学习目标
01
学习目标
理解无理数和实数的概念。
对实数进行分类,判断一个数是有理数还是无理数。
理解实数和数轴上的点一一对应。
新课教学
02
有理数知识点回顾
按整数和分数的关系分类:
按正数、负数、和零的关系分类:
知识回顾
上面的分数都可以写成有限小数或无限循环小数形式。
而任何一个有理数都可以写成有限小数或无限循环小数形式,
反之,有限小数和无限循环小数是有理数。
将下列分数写成小数的形式,你有什么发现?
,-
=0.75 ,-
=1.2
= 0.81818181… =0.81
新课引入
无理数
无限不循环的小数叫做无理数。
结合本章所学知识,举例:
无理数的分类:
结合无理数概念,举例:
.333133343…,3.3456789…,…
1.圆周率π及一些含π的数是无理数。
2.含根号的数不一定是无理数。(例: 等)
【注意】
新知讲解
实数的分类
有理数和无理数统称为实数。
有限小数或无限循环小数
无限不循环小数
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示无理数的点吗?
新知讲解
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点O到达点O',点O' 对应的数是多少?
π
新知讲解
数轴上的点可以表示有理数,那它可以表示无理数吗,你能在数轴上画出表示的点吗?
0
1
2
3
4
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数。
新知讲解
小试牛刀
03
1.在实数中,无理数的个数为( )。
A.1个 B.2个 C.3个 D.4个
小试牛刀
B
2.下列说法不正确的是( ).
A.如果数轴上的点表示的数不是有理数,那么就一定是无理数
B.大小介于两个有理数之间的无理数有无数个
C.-1的立方是-1,立方根也是-1
D.两个实数,较大者的平方也较大
D
小试牛刀
3.如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心、正方形对角线的长为半径画弧,交数轴于点A,则点A表示的数是( ).
A.- B.2- C.1- D.1+
小试牛刀
B
4.下列说法正确的有( )
①数轴上任意一点都表示一个有理数;
②任意一个无理数都可以用数轴上的一个点来表示;
③任意一个实数都可以用数轴上的一个点来表示;
④有理数与数轴上的点一 一对应.
实数
实数
B
A.1个 B.2个 C.3 D.4个
小试牛刀
5.如图,数轴上A,B,C,D四点中,与-对应的点距离最近的是( ).
A.点A B.点B C.点C D.点D
小试牛刀
B
6.比较 与 的大小.
解:
∵2<4,
∴,即<2,
∴<0,
∴<0,
< .
小试牛刀
延伸拓展
04
1.把下列各数填在相应的大括号内.
.
非负整数:{ …};
整数:{ …};
负分数:{ …};
延伸拓展
1.把下列各数填在相应的大括号内.
正实数:{ …};
有理数:{ …};
无理数:{ …}.
.
延伸拓展
2.比较3,,的大小( )
A. 3<< B. 3<<
C. <3< D. <<3
3=<
3=>
C
延伸拓展
课堂小结
05
无限不循环小数
实数
无理数
实数的分类
实数与数轴上点的关系
实数的大小比较
课堂小结
(1)对实数进行分类时,某些数应先进行计算或化简,然后根据最后结果进行分类,不能看到带根号的数,就认为是无理数,不能看到有分数线的数,就认为是有理数. (2)在实数范围内,一个数不是有理数,那么它一定是无理数,反之亦成立.
课堂小结
(1)按定义分:
你能给实数分类吗?
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
课堂小结
(2)按大小分:
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
实数的分类有不同的方法,但不论用哪一种分类方法,都要做到不重不漏.
课堂小结
无理数与有理数的区别
(1)任何有理数都能化成分数(整数可以看成分母是1的分数),无理数不能化成分数.
(2)任何一个有理数都可以化成有限小数(把整数看成小数点后是0的小数)或无限循环小数,无理数是无限不循环小数.
课堂小结
谢谢观看!
