7.1.3《平面直角坐标系》 课件(共30张PPT)
文档属性
| 名称 | 7.1.3《平面直角坐标系》 课件(共30张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
平面直角坐标系
人教版数学 七年级下册
学习目标
01
学习目标
理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念,认识并能画出平面直角坐标系.。
会用坐标轴说明直角坐标系内点的位置。
新课教学
02
8 聪 到 饿 日 一 有 啊 !
7 的 我 是 发 搞 可 了 明
6 确 小 大 北 京 你 才 批
5 年 没 定 妈 , 爸 事 达
4 营 业 女 天 员 各 合 乎
3 由 于 嘿 毫 力 量 靠 孩
2 仍 真 击 歼 安 机 麻 生
1 然 往 亲 赌 东 门 密 棒
0 1 2 3 4 5 6 7 8
密码是:嘿,我真聪明!
文字密码游戏:如图,“往”字的位置记作(2,1),请你破解密码:(3,3),(5,5),(2,7),(2,2),(1,8),(8,7),(8,8).
知识回顾
实数和数轴上的点一 一对应:
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
-2
-1
0
1
2
实数与数轴上的点有怎样的关系?
新课引入
知识点:平面直角坐标系
0
1
2
3
4
-3
-2
-1
A
B
C
数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标.例如点 A 在数轴上的坐标为 -3,点 B 在数轴上的坐标为 2.
反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.例如,数轴上坐标为 4 的点是点 C.
新课引入
思考 类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?
新课引入
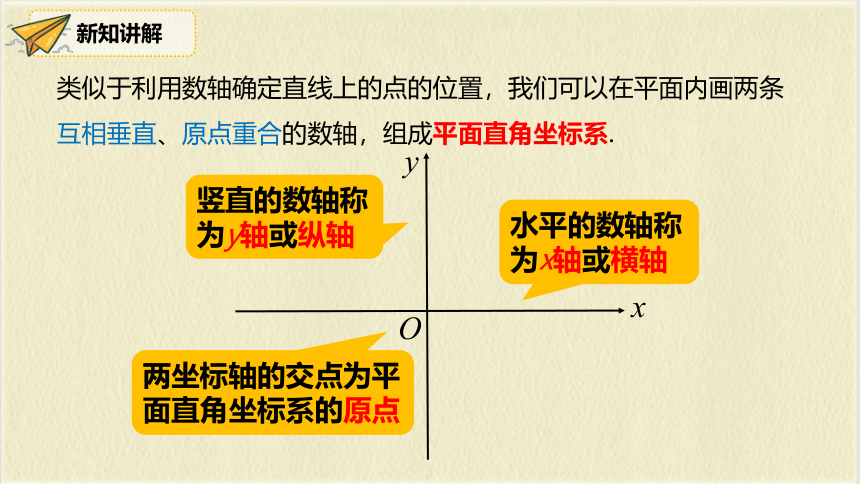
类似于利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
x
y
O
水平的数轴称为x轴或横轴
竖直的数轴称为y轴或纵轴
两坐标轴的交点为平面直角坐标系的原点
新知讲解
x
O
x轴
y轴
原点
y
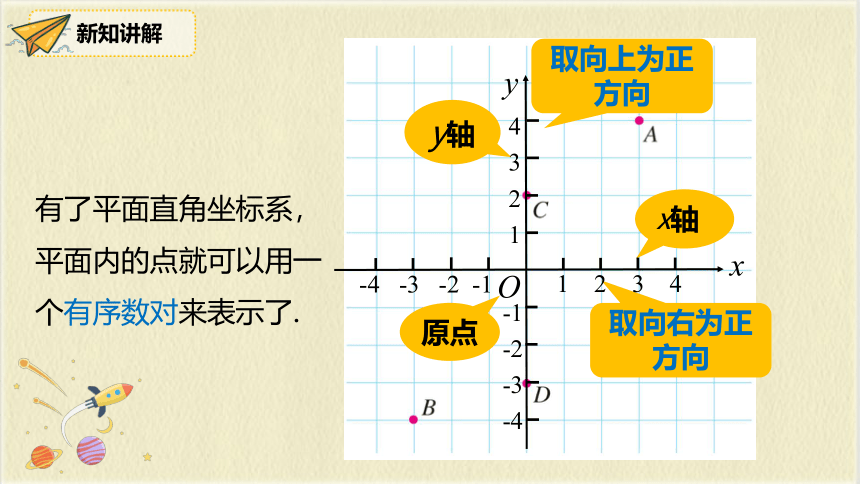
取向右为正方向
取向上为正方向
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了.
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
新知讲解
x
O
y
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
如图,由点 A 分别向 x 轴和y 轴作垂线,垂足 M 在 x 轴上的坐标是 3,垂足 N 在 y轴上的坐标是 4,我们说点 A 的横坐标是 3,纵坐标是 4,有序数对(3,4)就叫做点A 的坐标,记作 A(3,4).
M
N
新知讲解
x
O
y
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
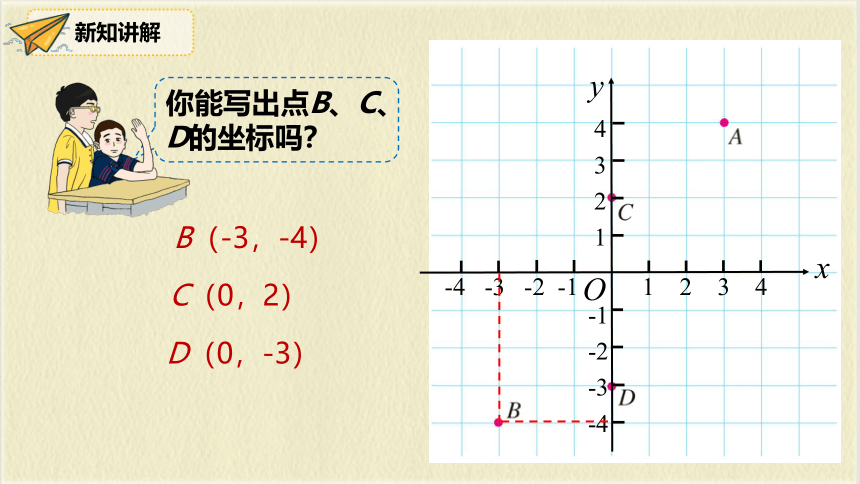
你能写出点B、C、D的坐标吗?
B(-3,-4)
C(0,2)
D(0,-3)
新知讲解
1.在写点的坐标时,横坐标在前,纵坐标在后,中间用逗号隔开,最后用小括号把它们括起来;
2.点的坐标是有序数对,(a,b)和(b,a)(a≠b)表示不同的点的坐标.
平面直角坐标系
新知讲解
小试牛刀
03
1.你能在图中找到坐标为(-3,2)的点吗?
x
O
y
-4
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
由坐标找点的方法
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
小试牛刀
2.下列四个选项中,关于平面直角坐标系的画法正确的是( )
两条数轴不垂直
x轴上数字错误
两条数轴没有正方向
D
小试牛刀
3.如图,平面直角坐标系中有 M、N、P、Q 四个点,其中与坐标(2,-3)对应的点是( )
A.M B.N C.P D.Q
x
O
y
-4
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
M
N
P
Q
C
小试牛刀
4.已知点 A(-1,-2)和点 B(3,m-1),如果直线 AB//x 轴,那么 m 的值为( )
A.1 B. -4 C. -1 D.3
点 A 和点 B 的纵坐标相等
-2 = m-1
m=-1
C
小试牛刀
5.如图,在平面直角坐标系中,
(1) 写出 A,B,C 三点的坐标;
(2) 描出点 D(2,-3),E(-2,4),F(0,-2).
x
O
y
-4
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
4
B
C
D
A
(4,3)
(-3,0)
(-4,-1)
E
F
小试牛刀
6.已知点 P 的坐标为(3a+6,2-a),且点 P 到两坐标轴的距离相等,则点 P 的坐标是_______________.
(3,3)或(-6,6)
|2-a|=|3a+6|
2-a=3a+6或2-a=-(3a+6)
a=-1或a=-4
(3,3)或(-6,6)
小试牛刀
延伸拓展
04
1.已知△ABC 的三个顶点的坐标分别是 A(0,1),B(2,0),C(2,3).
(1)在所给的平面直角坐标系中画出△ABC,△ABC 的面积为___;
x
1
2
3
8
-1
-2
-3
-5
4
5
6
7
y
O
-1
1
2
3
4
-4
9
-2
A
B
C
3
S△ABC=
延伸拓展
(2)点 P 在 x 轴上,且△ABP 的面积等于△ABC 的面积,求点 P 的坐标.
解:∵ △ABP 的面积等于△ABC 的面积,
∴ ,
解得 BP=6,
∴ 点 P 的坐标为(-4,0)或(8,0).
x
1
2
3
8
-1
-2
-3
-5
4
5
6
7
y
O
-1
1
2
3
4
-4
9
-2
A
B
C
延伸拓展
2.如图,四边形 ABCO 在平面直角坐标系中,A (1,2),B (5,4),C (6,0),O(0,0),求四边形 ABCO 的面积.
解:如图所示,过点 A 作 AD⊥x 轴于点 D,
过点 B 作 BE⊥x 轴于点 E,
则AD =2,OD =1,DE =4,CE =1,BE=4.
所以 S四边形ABCO=S三角形AOD+S梯形ABED+S三角形BEC
=×1×2+ ×(2+4)×4+ ×1×4
=1+12+2=15. 故四边形 ABCO 的面积为 15.
E
D
还有其他方法吗?
延伸拓展
解:如图,过点 B 作 BG⊥y 轴于点 G,连接 AG,
则 OG=4,BG=5,OC=6.
所以S四边形ABCO=S梯形BGOC-S三角形AOG-S三角形ABG
=×(5+6)×4- ×4×1- ×5×2
=22-2-5=15.
G
采用“补形法”
延伸拓展
课堂小结
05
水平的数轴称为 x 轴或横轴,
竖直的数轴称为 y 轴或纵轴
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系
两坐标轴的交点为平面直角坐标系的原点
平面直角坐标系
概念
原点
坐标轴
点的坐标
由点的坐标确定点的位置
由点的位置确定点的坐标
课堂小结
平面直角坐标系
1.坐标平面内的点和有序数对是一一对应的,即对于坐标平面内任意一点 M,都有唯一的一对有序实数(x,y)(即点 M 的坐标)和它对应;反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点 M (即坐标为(x,y)的点)和它对应.
2.点(x,y)到 x 轴的距离是 | y |,到 y 轴的距离是 | x |.
课堂小结
求平面直角坐标系中几何图形面积的方法
(1)当三角形有一条边平行于坐标轴或落在坐标轴上时,直接应用三角形的面积公式进行计算;
(2)当三角形没有一条边平行于坐标轴或落在坐标轴上时,要用“割补法”,将三角形的面积转化为其他图形面积的和或差;
(3)求不规则多边形的面积时,一般采用“割补法”,将不规则的多边形割补为规则图形,进而求出其面积.
课堂小结
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
平面直角坐标系
人教版数学 七年级下册
学习目标
01
学习目标
理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念,认识并能画出平面直角坐标系.。
会用坐标轴说明直角坐标系内点的位置。
新课教学
02
8 聪 到 饿 日 一 有 啊 !
7 的 我 是 发 搞 可 了 明
6 确 小 大 北 京 你 才 批
5 年 没 定 妈 , 爸 事 达
4 营 业 女 天 员 各 合 乎
3 由 于 嘿 毫 力 量 靠 孩
2 仍 真 击 歼 安 机 麻 生
1 然 往 亲 赌 东 门 密 棒
0 1 2 3 4 5 6 7 8
密码是:嘿,我真聪明!
文字密码游戏:如图,“往”字的位置记作(2,1),请你破解密码:(3,3),(5,5),(2,7),(2,2),(1,8),(8,7),(8,8).
知识回顾
实数和数轴上的点一 一对应:
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
-2
-1
0
1
2
实数与数轴上的点有怎样的关系?
新课引入
知识点:平面直角坐标系
0
1
2
3
4
-3
-2
-1
A
B
C
数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标.例如点 A 在数轴上的坐标为 -3,点 B 在数轴上的坐标为 2.
反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了.例如,数轴上坐标为 4 的点是点 C.
新课引入
思考 类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?
新课引入
类似于利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
x
y
O
水平的数轴称为x轴或横轴
竖直的数轴称为y轴或纵轴
两坐标轴的交点为平面直角坐标系的原点
新知讲解
x
O
x轴
y轴
原点
y
取向右为正方向
取向上为正方向
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了.
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
新知讲解
x
O
y
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
如图,由点 A 分别向 x 轴和y 轴作垂线,垂足 M 在 x 轴上的坐标是 3,垂足 N 在 y轴上的坐标是 4,我们说点 A 的横坐标是 3,纵坐标是 4,有序数对(3,4)就叫做点A 的坐标,记作 A(3,4).
M
N
新知讲解
x
O
y
1 2 3 4
-4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
你能写出点B、C、D的坐标吗?
B(-3,-4)
C(0,2)
D(0,-3)
新知讲解
1.在写点的坐标时,横坐标在前,纵坐标在后,中间用逗号隔开,最后用小括号把它们括起来;
2.点的坐标是有序数对,(a,b)和(b,a)(a≠b)表示不同的点的坐标.
平面直角坐标系
新知讲解
小试牛刀
03
1.你能在图中找到坐标为(-3,2)的点吗?
x
O
y
-4
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
由坐标找点的方法
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
小试牛刀
2.下列四个选项中,关于平面直角坐标系的画法正确的是( )
两条数轴不垂直
x轴上数字错误
两条数轴没有正方向
D
小试牛刀
3.如图,平面直角坐标系中有 M、N、P、Q 四个点,其中与坐标(2,-3)对应的点是( )
A.M B.N C.P D.Q
x
O
y
-4
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
M
N
P
Q
C
小试牛刀
4.已知点 A(-1,-2)和点 B(3,m-1),如果直线 AB//x 轴,那么 m 的值为( )
A.1 B. -4 C. -1 D.3
点 A 和点 B 的纵坐标相等
-2 = m-1
m=-1
C
小试牛刀
5.如图,在平面直角坐标系中,
(1) 写出 A,B,C 三点的坐标;
(2) 描出点 D(2,-3),E(-2,4),F(0,-2).
x
O
y
-4
-3
-2
-1
1
2
3
1
2
3
4
-1
-2
-3
4
B
C
D
A
(4,3)
(-3,0)
(-4,-1)
E
F
小试牛刀
6.已知点 P 的坐标为(3a+6,2-a),且点 P 到两坐标轴的距离相等,则点 P 的坐标是_______________.
(3,3)或(-6,6)
|2-a|=|3a+6|
2-a=3a+6或2-a=-(3a+6)
a=-1或a=-4
(3,3)或(-6,6)
小试牛刀
延伸拓展
04
1.已知△ABC 的三个顶点的坐标分别是 A(0,1),B(2,0),C(2,3).
(1)在所给的平面直角坐标系中画出△ABC,△ABC 的面积为___;
x
1
2
3
8
-1
-2
-3
-5
4
5
6
7
y
O
-1
1
2
3
4
-4
9
-2
A
B
C
3
S△ABC=
延伸拓展
(2)点 P 在 x 轴上,且△ABP 的面积等于△ABC 的面积,求点 P 的坐标.
解:∵ △ABP 的面积等于△ABC 的面积,
∴ ,
解得 BP=6,
∴ 点 P 的坐标为(-4,0)或(8,0).
x
1
2
3
8
-1
-2
-3
-5
4
5
6
7
y
O
-1
1
2
3
4
-4
9
-2
A
B
C
延伸拓展
2.如图,四边形 ABCO 在平面直角坐标系中,A (1,2),B (5,4),C (6,0),O(0,0),求四边形 ABCO 的面积.
解:如图所示,过点 A 作 AD⊥x 轴于点 D,
过点 B 作 BE⊥x 轴于点 E,
则AD =2,OD =1,DE =4,CE =1,BE=4.
所以 S四边形ABCO=S三角形AOD+S梯形ABED+S三角形BEC
=×1×2+ ×(2+4)×4+ ×1×4
=1+12+2=15. 故四边形 ABCO 的面积为 15.
E
D
还有其他方法吗?
延伸拓展
解:如图,过点 B 作 BG⊥y 轴于点 G,连接 AG,
则 OG=4,BG=5,OC=6.
所以S四边形ABCO=S梯形BGOC-S三角形AOG-S三角形ABG
=×(5+6)×4- ×4×1- ×5×2
=22-2-5=15.
G
采用“补形法”
延伸拓展
课堂小结
05
水平的数轴称为 x 轴或横轴,
竖直的数轴称为 y 轴或纵轴
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系
两坐标轴的交点为平面直角坐标系的原点
平面直角坐标系
概念
原点
坐标轴
点的坐标
由点的坐标确定点的位置
由点的位置确定点的坐标
课堂小结
平面直角坐标系
1.坐标平面内的点和有序数对是一一对应的,即对于坐标平面内任意一点 M,都有唯一的一对有序实数(x,y)(即点 M 的坐标)和它对应;反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点 M (即坐标为(x,y)的点)和它对应.
2.点(x,y)到 x 轴的距离是 | y |,到 y 轴的距离是 | x |.
课堂小结
求平面直角坐标系中几何图形面积的方法
(1)当三角形有一条边平行于坐标轴或落在坐标轴上时,直接应用三角形的面积公式进行计算;
(2)当三角形没有一条边平行于坐标轴或落在坐标轴上时,要用“割补法”,将三角形的面积转化为其他图形面积的和或差;
(3)求不规则多边形的面积时,一般采用“割补法”,将不规则的多边形割补为规则图形,进而求出其面积.
课堂小结
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
