宁夏青铜峡市高中2021-2022学年高二上学期期末考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 宁夏青铜峡市高中2021-2022学年高二上学期期末考试数学(理)试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 732.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-13 00:00:00 | ||
图片预览

文档简介
青铜峡市高中2021-2022学年高二上学期期末考试
数学理试题
一:选择题:共12小题.(每小题5分,共计60分,在每个小题给出的四个选项中,只有一项是符合题目要求的).
1.椭圆=1的焦点坐标为( )
A.(0,﹣4),(0,4) B.(0,),(0,﹣)
C.(4,0),(﹣4,0) D.(,0),(﹣,0)
2.在样本的频率分布直方图中,某个小长方形的面积是其他小长方形面积之和的,已知样本容量是80,则该组的频数为( )
A.20 B.16 C.30 D.35
3.抛物线的准线方程是,则( )
A. B. C.8 D.– 8
4.如图,在平行六面体中,M为与的交点,若.则下列向量中与相等的向量是( )
A. B. C. D.
5. 下列命题正确的是( )
A. “”是“”的充分不必要条件
B. 命题“”为假命题,则命题p与命题q都是假命题
C. “”是“”成立的必要不充分条件
D. 命题“存在,使得”的否定是:“对任意,均有
6.若以双曲线的左焦点为圆心,以左焦点到右顶点的距离为半径的圆的方程为,则该双曲线的方程为( )
A. B. C. D.
7.已知两圆:,:,动圆和圆内切,和圆外切,则动圆圆心的轨迹方程为( )
A. B. C. D.
8.半径为的半圆卷成一个圆锥,则它的体积为( )
A. B. C. D.
9.已知命题p:关于x的方程+ax+1=0没有实根;命题q: x>0, .若“┐p”和“p∧q”都是假命题,则实数a的取值范围是( )
A.(-∞,-2)∪(1,+∞) B.(-2,1] C.(1,2) D.(1,+∞)
10.阿基米德(公元前287年﹣公元前212年),古希腊伟大的哲学家、数学家、物理学家、力学家.他发展的“逼近法”为近代的“微积分”的创立奠定了基础.他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆C的焦点在x轴上,且椭圆C的离心率为,面积为,则椭圆C的方程为( )
A. B. C. D.
11. 已知倾斜角为直线经过抛物线的焦点,且与抛物线相交于两点弦的
长为 ( )
A. B. C. D.
12.已知为椭圆的一个焦点,是短轴的一个端点,线段的延长线交椭圆于点,
且,则椭圆的离心率为( )
B. C. D.
二、填空题(本题共4小题,每小题5分,共20分)
13.抛物线的焦点到双曲线的渐近线的距离是
14. 经过点且与双曲线有相同渐近线的双曲线方程是
15. 已知椭圆 ,过点P(1,1)的直线l与椭圆C交于A,B两点,若点P恰为弦AB中点,则直线l斜率是______________
16.已知是抛物线上一点,为其焦点,点,则的最小值是 .
三、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)3名男生,4名女生,按照不同的要求排队,求不同的排队方案的方法种数?
(1)选其中5人排成一排;
(2)全体站成一排,男、女各站在一起;
(3)全体站成一排,男生不能站在一起.
18.(12分)在圆上任取一点P,过P作x轴的垂线PD,D为垂足.当点P在圆上运动时,
(1)求线段PD的中点Q的轨迹方程.
(2)若直线与(1)中的Q的轨迹交于A,B两点,求
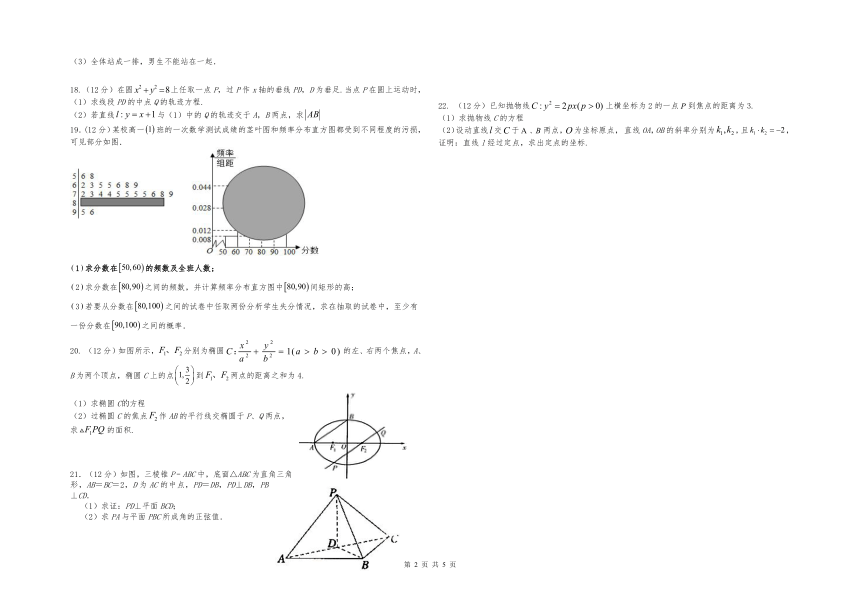
19.(12分)某校高一班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
1求分数在的频数及全班人数;
2求分数在之间的频数,并计算频率分布直方图中间矩形的高;
3若要从分数在之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在之间的概率.
20. (12分)如图所示,分别为椭圆的左、右两个焦点,A、B为两个顶点,椭圆C上的点到两点的距离之和为4.
(1)求椭圆C方程
(2)过椭圆C的焦点作AB的平行线交椭圆于P、Q两点,求的面积.
21.(12分)如图,三棱锥P﹣ABC中,底面△ABC为直角三角形,AB=BC=2,D为AC的中点,PD=DB,PD⊥DB,PB⊥CD.
(1)求证:PD⊥平面BCD;
(2)求PA与平面PBC所成角的正弦值.
22. (12分)已知抛物线上横坐标为2的一点到焦点的距离为3.
(1)求抛物线C的方程
(2)设动直线交于、两点,为坐标原点, 直线OA,OB的斜率分别为,且,证明:直线l经过定点,求出定点的坐标.
青铜峡市高中2021-2022学年高二上学期期末考试
数学理试题答案
一:选择题:共12小题.(每小题5分,共计60分,在每个小题给出的四个选项中,只有一项是符合题目要求的).
1 2 3 4 5 6 7 8 9 10 11 12
A B B A A C D A C A B B
二、填空题(本题共4小题,每小题5分,共20分)
13 14 15. 16. 6
三、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)3名男生,4名女生,按照不同的要求排队,求不同的排队方案的方法种数?
(1)选其中5人排成一排;
(2)全体站成一排,男、女各站在一起;
(3)全体站成一排,男生不能站在一起.
解:(1)从7个元素中选出5个全排列,有=2 520种排法.
(2)男生必须站在一起,是男生的全排列,有种排法;女生必须站在一起,是女生的全排列,有种排法;全体男生、女生各视为一个元素,有种排法,由分步乘法计数原理知,共有N==288(种).
(3):先安排女生共有种排法,男生在4个女生隔成的五个空中安排共有种排法,故N==1 440(种).
18.(12分)在圆上任取一点P,过P作x轴的垂线PD,D为垂足.当点P在圆上运动时,
(1)求线段PD的中点Q的轨迹方程.
(2)若直线与(1)中的Q的轨迹交于A,B两点,求
【解】(1)设,,,
是PD的中点, ,,
又P在圆上, ,
即, .
线段PD的中点的轨迹方程是.
(2)由(1)知动点轨迹方程为,
故,
得,
设,,
则,,
所以.
19.(12分)某校高一班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
1求分数在的频数及全班人数;
2求分数在之间的频数,并计算频率分布直方图中间矩形的高;
3若要从分数在之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在之间的概率.
【详解】
1分数在的频率为,由茎叶图知:分数在之间的频数为2,
全班人数为.
2分数在之间的频数为;
频率分布直方图中间的矩形的高为.
3将之间的3个分数编号为,,,之间的2个分数编号为,,
在之间的试卷中任取两份的基本事件为:
,,,,,,,,,共10个,
其中,至少有一个在之间的基本事件有7个,
故至少有一份分数在之间的概率是.
20. (12分)如图所示,分别为椭圆的左、右两个焦点,A、B为两个顶点,椭圆C上的点到两点的距离之和为4.
(1)求椭圆C方程
(2)过椭圆C的焦点作AB的平行线交椭圆于P、Q两点,求的面积.
【详解】解:(1)由题设知:2a = 4,即a = 2, 将点代入椭圆方程得 ,
解得b2 = 3,∴c2 = a2-b2 = 4-3 = 1,
故椭圆方程为;焦点F1、F2的坐标分别为(-1,0)和(1,0);
(2)由(1)知,,
∴PQ所在直线方程为,
由得 ,设P (x1,y1),Q (x2,y2),则,
21.(12分)如图,三棱锥P﹣ABC中,底面△ABC为直角三角形,AB=BC=2,D为AC的中点,PD=DB,PD⊥DB,PB⊥CD.
(1)求证:PD⊥平面BCD;
(2)求PA与平面PBC所成角的正弦值.
【解答】(1)证明:∵AB=BC,D为AC的中点,∴BD⊥CD,
∵PB⊥CD,BD∩PB=D,BD、PB 平面PBD,
∴CD⊥平面PBD,
∵PD 平面PBD,∴CD⊥PD,
又PD⊥DB,CD∩DB=D,CD、DB 平面BCD,
∴PD⊥平面BCD.
(2)解:由(1)知,PD⊥平面BCD,BD⊥AC,
故以D为原点,DA,DB,DP所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
则A(,0,0),B(0,,0),C(﹣,0,0),P(0,0,),
∴=(,0,﹣),=(0,,﹣),=(﹣,0,﹣),
设平面PBC的法向量为=(x,y,z),则,即,
令z=1,则x=﹣1,y=1,∴=(﹣1,1,1),
设PA与平面PBC所成角为θ,则sinθ=|cos<,>|=||=||=,
故PA与平面PBC所成角的正弦值为.
22. (12分)已知抛物线上横坐标为2的一点到焦点的距离为3.
(1)求抛物线C的方程
(2)设动直线交于、两点,为坐标原点, 直线OA,OB的斜率分别为,且,证明:直线l经过定点,求出定点的坐标.
【详解】(1)抛物线的准线方程为:,
由抛物线的定义可得:,解得:,
所以抛物线的标准方程为:
(2)证明:设直线的方程为,,
代入抛物线方程化简得,
∴. ,
∵,
解得: ∴直线经过定点,且定点为.
数学理试题
一:选择题:共12小题.(每小题5分,共计60分,在每个小题给出的四个选项中,只有一项是符合题目要求的).
1.椭圆=1的焦点坐标为( )
A.(0,﹣4),(0,4) B.(0,),(0,﹣)
C.(4,0),(﹣4,0) D.(,0),(﹣,0)
2.在样本的频率分布直方图中,某个小长方形的面积是其他小长方形面积之和的,已知样本容量是80,则该组的频数为( )
A.20 B.16 C.30 D.35
3.抛物线的准线方程是,则( )
A. B. C.8 D.– 8
4.如图,在平行六面体中,M为与的交点,若.则下列向量中与相等的向量是( )
A. B. C. D.
5. 下列命题正确的是( )
A. “”是“”的充分不必要条件
B. 命题“”为假命题,则命题p与命题q都是假命题
C. “”是“”成立的必要不充分条件
D. 命题“存在,使得”的否定是:“对任意,均有
6.若以双曲线的左焦点为圆心,以左焦点到右顶点的距离为半径的圆的方程为,则该双曲线的方程为( )
A. B. C. D.
7.已知两圆:,:,动圆和圆内切,和圆外切,则动圆圆心的轨迹方程为( )
A. B. C. D.
8.半径为的半圆卷成一个圆锥,则它的体积为( )
A. B. C. D.
9.已知命题p:关于x的方程+ax+1=0没有实根;命题q: x>0, .若“┐p”和“p∧q”都是假命题,则实数a的取值范围是( )
A.(-∞,-2)∪(1,+∞) B.(-2,1] C.(1,2) D.(1,+∞)
10.阿基米德(公元前287年﹣公元前212年),古希腊伟大的哲学家、数学家、物理学家、力学家.他发展的“逼近法”为近代的“微积分”的创立奠定了基础.他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆C的焦点在x轴上,且椭圆C的离心率为,面积为,则椭圆C的方程为( )
A. B. C. D.
11. 已知倾斜角为直线经过抛物线的焦点,且与抛物线相交于两点弦的
长为 ( )
A. B. C. D.
12.已知为椭圆的一个焦点,是短轴的一个端点,线段的延长线交椭圆于点,
且,则椭圆的离心率为( )
B. C. D.
二、填空题(本题共4小题,每小题5分,共20分)
13.抛物线的焦点到双曲线的渐近线的距离是
14. 经过点且与双曲线有相同渐近线的双曲线方程是
15. 已知椭圆 ,过点P(1,1)的直线l与椭圆C交于A,B两点,若点P恰为弦AB中点,则直线l斜率是______________
16.已知是抛物线上一点,为其焦点,点,则的最小值是 .
三、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)3名男生,4名女生,按照不同的要求排队,求不同的排队方案的方法种数?
(1)选其中5人排成一排;
(2)全体站成一排,男、女各站在一起;
(3)全体站成一排,男生不能站在一起.
18.(12分)在圆上任取一点P,过P作x轴的垂线PD,D为垂足.当点P在圆上运动时,
(1)求线段PD的中点Q的轨迹方程.
(2)若直线与(1)中的Q的轨迹交于A,B两点,求
19.(12分)某校高一班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
1求分数在的频数及全班人数;
2求分数在之间的频数,并计算频率分布直方图中间矩形的高;
3若要从分数在之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在之间的概率.
20. (12分)如图所示,分别为椭圆的左、右两个焦点,A、B为两个顶点,椭圆C上的点到两点的距离之和为4.
(1)求椭圆C方程
(2)过椭圆C的焦点作AB的平行线交椭圆于P、Q两点,求的面积.
21.(12分)如图,三棱锥P﹣ABC中,底面△ABC为直角三角形,AB=BC=2,D为AC的中点,PD=DB,PD⊥DB,PB⊥CD.
(1)求证:PD⊥平面BCD;
(2)求PA与平面PBC所成角的正弦值.
22. (12分)已知抛物线上横坐标为2的一点到焦点的距离为3.
(1)求抛物线C的方程
(2)设动直线交于、两点,为坐标原点, 直线OA,OB的斜率分别为,且,证明:直线l经过定点,求出定点的坐标.
青铜峡市高中2021-2022学年高二上学期期末考试
数学理试题答案
一:选择题:共12小题.(每小题5分,共计60分,在每个小题给出的四个选项中,只有一项是符合题目要求的).
1 2 3 4 5 6 7 8 9 10 11 12
A B B A A C D A C A B B
二、填空题(本题共4小题,每小题5分,共20分)
13 14 15. 16. 6
三、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)3名男生,4名女生,按照不同的要求排队,求不同的排队方案的方法种数?
(1)选其中5人排成一排;
(2)全体站成一排,男、女各站在一起;
(3)全体站成一排,男生不能站在一起.
解:(1)从7个元素中选出5个全排列,有=2 520种排法.
(2)男生必须站在一起,是男生的全排列,有种排法;女生必须站在一起,是女生的全排列,有种排法;全体男生、女生各视为一个元素,有种排法,由分步乘法计数原理知,共有N==288(种).
(3):先安排女生共有种排法,男生在4个女生隔成的五个空中安排共有种排法,故N==1 440(种).
18.(12分)在圆上任取一点P,过P作x轴的垂线PD,D为垂足.当点P在圆上运动时,
(1)求线段PD的中点Q的轨迹方程.
(2)若直线与(1)中的Q的轨迹交于A,B两点,求
【解】(1)设,,,
是PD的中点, ,,
又P在圆上, ,
即, .
线段PD的中点的轨迹方程是.
(2)由(1)知动点轨迹方程为,
故,
得,
设,,
则,,
所以.
19.(12分)某校高一班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
1求分数在的频数及全班人数;
2求分数在之间的频数,并计算频率分布直方图中间矩形的高;
3若要从分数在之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在之间的概率.
【详解】
1分数在的频率为,由茎叶图知:分数在之间的频数为2,
全班人数为.
2分数在之间的频数为;
频率分布直方图中间的矩形的高为.
3将之间的3个分数编号为,,,之间的2个分数编号为,,
在之间的试卷中任取两份的基本事件为:
,,,,,,,,,共10个,
其中,至少有一个在之间的基本事件有7个,
故至少有一份分数在之间的概率是.
20. (12分)如图所示,分别为椭圆的左、右两个焦点,A、B为两个顶点,椭圆C上的点到两点的距离之和为4.
(1)求椭圆C方程
(2)过椭圆C的焦点作AB的平行线交椭圆于P、Q两点,求的面积.
【详解】解:(1)由题设知:2a = 4,即a = 2, 将点代入椭圆方程得 ,
解得b2 = 3,∴c2 = a2-b2 = 4-3 = 1,
故椭圆方程为;焦点F1、F2的坐标分别为(-1,0)和(1,0);
(2)由(1)知,,
∴PQ所在直线方程为,
由得 ,设P (x1,y1),Q (x2,y2),则,
21.(12分)如图,三棱锥P﹣ABC中,底面△ABC为直角三角形,AB=BC=2,D为AC的中点,PD=DB,PD⊥DB,PB⊥CD.
(1)求证:PD⊥平面BCD;
(2)求PA与平面PBC所成角的正弦值.
【解答】(1)证明:∵AB=BC,D为AC的中点,∴BD⊥CD,
∵PB⊥CD,BD∩PB=D,BD、PB 平面PBD,
∴CD⊥平面PBD,
∵PD 平面PBD,∴CD⊥PD,
又PD⊥DB,CD∩DB=D,CD、DB 平面BCD,
∴PD⊥平面BCD.
(2)解:由(1)知,PD⊥平面BCD,BD⊥AC,
故以D为原点,DA,DB,DP所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
则A(,0,0),B(0,,0),C(﹣,0,0),P(0,0,),
∴=(,0,﹣),=(0,,﹣),=(﹣,0,﹣),
设平面PBC的法向量为=(x,y,z),则,即,
令z=1,则x=﹣1,y=1,∴=(﹣1,1,1),
设PA与平面PBC所成角为θ,则sinθ=|cos<,>|=||=||=,
故PA与平面PBC所成角的正弦值为.
22. (12分)已知抛物线上横坐标为2的一点到焦点的距离为3.
(1)求抛物线C的方程
(2)设动直线交于、两点,为坐标原点, 直线OA,OB的斜率分别为,且,证明:直线l经过定点,求出定点的坐标.
【详解】(1)抛物线的准线方程为:,
由抛物线的定义可得:,解得:,
所以抛物线的标准方程为:
(2)证明:设直线的方程为,,
代入抛物线方程化简得,
∴. ,
∵,
解得: ∴直线经过定点,且定点为.
同课章节目录
