2021-2022学年高一上学期数学人教A版(2019)必修第一册5.7三角函数的应用同步练习word版无答案
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.7三角函数的应用同步练习word版无答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 00:00:00 | ||
图片预览


文档简介
5.7 三角函数的应用 同步练习
一、选择题
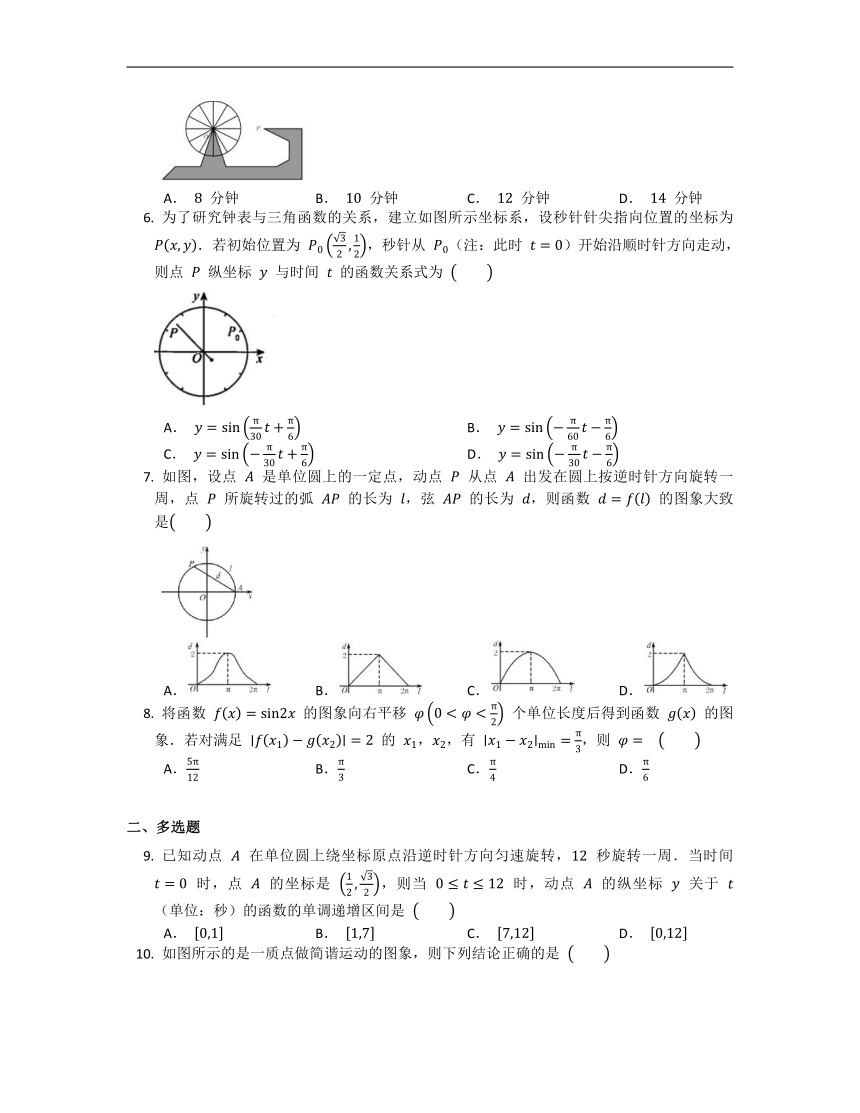
电流 随时间 变化的关系式是 ,则当 时,电流 为
A. B. C. D.
如图,某港口一天 时到 时的水深变化曲线近似满足函数 .据此函数可知,这段时间水深(单位:)的最大值为
A. B. C. D.
动点 在圆 上绕坐标原点沿逆时针方向匀速旋转, 秒旋转一周,已知时间 时,点 的坐标是 ,则当 时,动点 的纵坐标 关于 (单位:秒)的函数的单调递增区间是
A. B.
C. D.
某港口某天 时至 时的水深 (米)随时间 (时)变化曲线近似满足如下函数模型:.若该港口在该天 时至 时内,有且只有 个时刻水深为 米,则该港口该天水最深的时刻不可能为
时 B. 时 C. 时 D. 时
如图,一个摩天轮的半径为 ,轮子的最低处距离地面 .如果此摩天轮按逆时针匀速转动,每 分钟转一圈,且当摩天轮上某人经过点 (点 与摩天轮中心 的高度相同)时开始计时.在摩天轮转动的一圈内,此人相对于地面的高度不小于 的时间大约是
A. 分钟 B. 分钟 C. 分钟 D. 分钟
为了研究钟表与三角函数的关系,建立如图所示坐标系,设秒针针尖指向位置的坐标为 .若初始位置为 ,秒针从 (注:此时 )开始沿顺时针方向走动,则点 纵坐标 与时间 的函数关系式为
A. B.
C. D.
如图,设点 是单位圆上的一定点,动点 从点 出发在圆上按逆时针方向旋转一周,点 所旋转过的弧 的长为 ,弦 的长为 ,则函数 的图象大致是
A. B. C. D.
将函数 的图象向右平移 个单位长度后得到函数 的图象.若对满足 的 ,,有 ,则
A. B. C. D.
二、多选题
已知动点 在单位圆上绕坐标原点沿逆时针方向匀速旋转, 秒旋转一周.当时间 时,点 的坐标是 ,则当 时,动点 的纵坐标 关于 (单位:秒)的函数的单调递增区间是
A. B. C. D.
如图所示的是一质点做简谐运动的图象,则下列结论正确的是
A.该质点的运动周期为
B.该质点的振幅为
C.该质点在 和 时运动速度为零
D.该质点在 和 时运动速度为零
如图所示是一质点做简谐运动的图象,则下列结论正确的是
A.该质点的运动周期为
B.该质点的振幅为
C.该质点在 和 时运动速度最大
D.该质点在 和 时运动速度为零
某时钟的秒针端点 到时钟的中心点 的距离为 ,秒针均匀地绕点 旋转.当时间 时,点 与钟面上标“”的点 重合,将 , 两点的距离 表示成 的函数,其中 ,则
A. B.
C. D.
三、填空题
函数 的图象的一条对称轴方程是 .
砖雕是我国古建筑雕刻中很重要的一种艺术形式,传统砖雕精致细腻、气韵生动、极富书卷气,如图是一扇环形砖雕,可视为扇形 截去同心扇形 所得部分,已知 ,,,则该扇环形砖雕的面积为 .
有一小球从某点开始来回摆动,离开平衡位置的位移 (单位:)关于时间 (单位:)的函数解析式是 ,函数图象如图所示.则函数的解析式为 .
如图,, 为某市的两个旅游中心,海岸线 可看做一条直线,且与 所在直线平行,现计划将两个旅游中心与海岸线连接起来,由于地势原因,需在以 为直径的半圆上选定一点 ,修建 ,, 三段公路,其中 ,,两平行直线 与 之间的距离为 ,公路 和 段的造价均为 ,公路 段的造价为 ,为便于筹备充足资金,需要计算该项工程的最大预算,根据以上信息,这三段公路总造价的最大值为
千万.
解答题
一台发电机产生的电流是正弦式电流,电压和时间之间的关系如图所示.由图象说出它的周期、频率和电压的最大值,并求出电压 (单位:)关于时间 (单位:)的函数解析式.
一根长为 的线,一端固定,另一端悬挂一个小球,组成一个单摆,小球摆动时,离开平衡位置的位移 (单位:)与时间 (单位:)的函数关系是 ,.
(1) 求小球摆动的周期和频率;
(2) 已知 ,要使小球摆动的周期恰好是 ,则线的长度 应当是多少?
如图, 是半径为 ,圆心角为 的扇形, 是扇形弧上的一动点.记 ,四边形 的面积为 .
(1) 找出 与 的函数关系;
(2) 当 取何值时, 最大,并求出这个最大值.
如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为 米,圆环的圆心 距离地面的高度为 米,蚂蚁爬行一圈需要 分钟,且蚂蚁的起始位置在最低点 处.
(1) 试写出蚂蚁距离地面的高度 (米)关于时刻 (分钟)的函数关系式 ;
(2) 在蚂蚁绕圆环爬行一圈的时间内,有多长时间蚂蚁距离地面超过 米?
某园林单位准备绿化一块直径为 的半圆形空地, 外的地方种草, 的内接正方形 为一水池,其余的地方种花.若 ,,设 的面积为 ,正方形的面积为 .
(1) 用 , 表示 和 ;
(2) 当 固定, 变化时,求 取最小值时的角 .
某公司要在一条笔直的道路边安装路灯,要求灯柱 与地面垂直,灯杆 与灯柱 所在的平面与道路走向垂,路灯 采用锥形灯罩,射出的光线与平面 的部分截面如图中阴影部分所示.已知 ,,路宽 米.设 .
(1) 求灯柱 的高 (用 表示);
(2) 此公司应该如何设置 的值才能使制造路灯灯柱 与灯杆 所用材料的总长度最小?最小值为多少?(结果精确到 米)
一、选择题
电流 随时间 变化的关系式是 ,则当 时,电流 为
A. B. C. D.
如图,某港口一天 时到 时的水深变化曲线近似满足函数 .据此函数可知,这段时间水深(单位:)的最大值为
A. B. C. D.
动点 在圆 上绕坐标原点沿逆时针方向匀速旋转, 秒旋转一周,已知时间 时,点 的坐标是 ,则当 时,动点 的纵坐标 关于 (单位:秒)的函数的单调递增区间是
A. B.
C. D.
某港口某天 时至 时的水深 (米)随时间 (时)变化曲线近似满足如下函数模型:.若该港口在该天 时至 时内,有且只有 个时刻水深为 米,则该港口该天水最深的时刻不可能为
时 B. 时 C. 时 D. 时
如图,一个摩天轮的半径为 ,轮子的最低处距离地面 .如果此摩天轮按逆时针匀速转动,每 分钟转一圈,且当摩天轮上某人经过点 (点 与摩天轮中心 的高度相同)时开始计时.在摩天轮转动的一圈内,此人相对于地面的高度不小于 的时间大约是
A. 分钟 B. 分钟 C. 分钟 D. 分钟
为了研究钟表与三角函数的关系,建立如图所示坐标系,设秒针针尖指向位置的坐标为 .若初始位置为 ,秒针从 (注:此时 )开始沿顺时针方向走动,则点 纵坐标 与时间 的函数关系式为
A. B.
C. D.
如图,设点 是单位圆上的一定点,动点 从点 出发在圆上按逆时针方向旋转一周,点 所旋转过的弧 的长为 ,弦 的长为 ,则函数 的图象大致是
A. B. C. D.
将函数 的图象向右平移 个单位长度后得到函数 的图象.若对满足 的 ,,有 ,则
A. B. C. D.
二、多选题
已知动点 在单位圆上绕坐标原点沿逆时针方向匀速旋转, 秒旋转一周.当时间 时,点 的坐标是 ,则当 时,动点 的纵坐标 关于 (单位:秒)的函数的单调递增区间是
A. B. C. D.
如图所示的是一质点做简谐运动的图象,则下列结论正确的是
A.该质点的运动周期为
B.该质点的振幅为
C.该质点在 和 时运动速度为零
D.该质点在 和 时运动速度为零
如图所示是一质点做简谐运动的图象,则下列结论正确的是
A.该质点的运动周期为
B.该质点的振幅为
C.该质点在 和 时运动速度最大
D.该质点在 和 时运动速度为零
某时钟的秒针端点 到时钟的中心点 的距离为 ,秒针均匀地绕点 旋转.当时间 时,点 与钟面上标“”的点 重合,将 , 两点的距离 表示成 的函数,其中 ,则
A. B.
C. D.
三、填空题
函数 的图象的一条对称轴方程是 .
砖雕是我国古建筑雕刻中很重要的一种艺术形式,传统砖雕精致细腻、气韵生动、极富书卷气,如图是一扇环形砖雕,可视为扇形 截去同心扇形 所得部分,已知 ,,,则该扇环形砖雕的面积为 .
有一小球从某点开始来回摆动,离开平衡位置的位移 (单位:)关于时间 (单位:)的函数解析式是 ,函数图象如图所示.则函数的解析式为 .
如图,, 为某市的两个旅游中心,海岸线 可看做一条直线,且与 所在直线平行,现计划将两个旅游中心与海岸线连接起来,由于地势原因,需在以 为直径的半圆上选定一点 ,修建 ,, 三段公路,其中 ,,两平行直线 与 之间的距离为 ,公路 和 段的造价均为 ,公路 段的造价为 ,为便于筹备充足资金,需要计算该项工程的最大预算,根据以上信息,这三段公路总造价的最大值为
千万.
解答题
一台发电机产生的电流是正弦式电流,电压和时间之间的关系如图所示.由图象说出它的周期、频率和电压的最大值,并求出电压 (单位:)关于时间 (单位:)的函数解析式.
一根长为 的线,一端固定,另一端悬挂一个小球,组成一个单摆,小球摆动时,离开平衡位置的位移 (单位:)与时间 (单位:)的函数关系是 ,.
(1) 求小球摆动的周期和频率;
(2) 已知 ,要使小球摆动的周期恰好是 ,则线的长度 应当是多少?
如图, 是半径为 ,圆心角为 的扇形, 是扇形弧上的一动点.记 ,四边形 的面积为 .
(1) 找出 与 的函数关系;
(2) 当 取何值时, 最大,并求出这个最大值.
如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为 米,圆环的圆心 距离地面的高度为 米,蚂蚁爬行一圈需要 分钟,且蚂蚁的起始位置在最低点 处.
(1) 试写出蚂蚁距离地面的高度 (米)关于时刻 (分钟)的函数关系式 ;
(2) 在蚂蚁绕圆环爬行一圈的时间内,有多长时间蚂蚁距离地面超过 米?
某园林单位准备绿化一块直径为 的半圆形空地, 外的地方种草, 的内接正方形 为一水池,其余的地方种花.若 ,,设 的面积为 ,正方形的面积为 .
(1) 用 , 表示 和 ;
(2) 当 固定, 变化时,求 取最小值时的角 .
某公司要在一条笔直的道路边安装路灯,要求灯柱 与地面垂直,灯杆 与灯柱 所在的平面与道路走向垂,路灯 采用锥形灯罩,射出的光线与平面 的部分截面如图中阴影部分所示.已知 ,,路宽 米.设 .
(1) 求灯柱 的高 (用 表示);
(2) 此公司应该如何设置 的值才能使制造路灯灯柱 与灯杆 所用材料的总长度最小?最小值为多少?(结果精确到 米)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
