2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册5.2 导数的运算 随堂训练word版含答案
文档属性
| 名称 | 2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册5.2 导数的运算 随堂训练word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 433.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 00:00:00 | ||
图片预览


文档简介
《导数的运算》随堂训练
夯实基础
知识点1:利用导数公式求函数的导数
1.下列求导运算不正确的是( )
A. B.
C. D.
2.给出下列结论:
①=-sin =-;
②若y=,则y′=-2x-3;
③若f(x)=3x,则[ f′(1)]′=3;
④若,则.
其中正确的个数是( )
A.1 B.2 C.3 D.4
知识点2:利用导数的运算法则求导数
3.已知函数,则等于( )
A.0 B.2 C. D.
4.函数y= (a>0)在x=x0处的导数为0,那么x0=( )
A.a B.±a C.-a D.a2
5.已知函数,若,的值为 ( )
A.4 B.5 C.6 D.7
知识点3:导数计算的综合应用
6.设函数,曲线在点处的切线方程为,则曲线在点处的切线的斜率为( )
A.4 B. C.2 D.
7.若,则等于( )
A. B.0 C. D.6
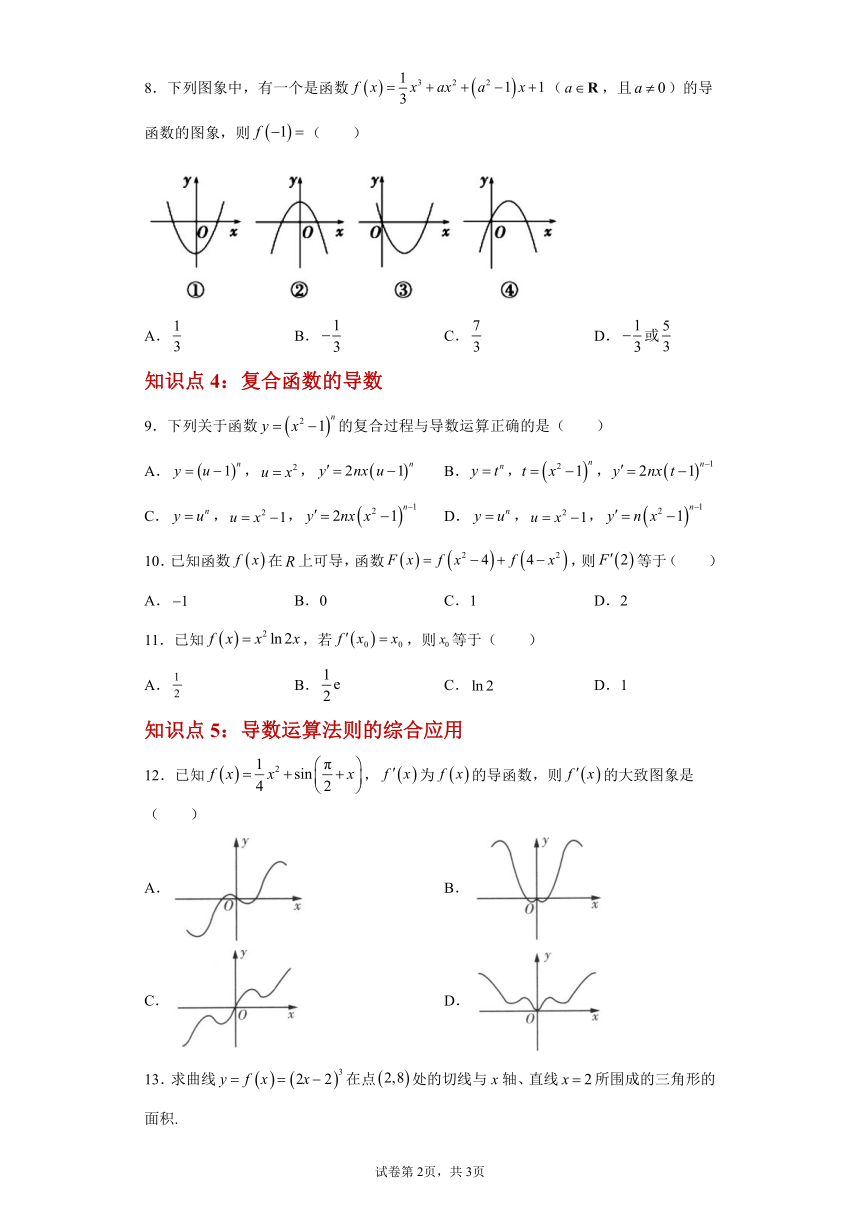
8.下列图象中,有一个是函数(,且)的导函数的图象,则( )
B. C. D.或
知识点4:复合函数的导数
9.下列关于函数的复合过程与导数运算正确的是( )
A.,, B.,,
C.,, D.,,
10.已知函数在上可导,函数,则等于( )
A. B.0 C.1 D.2
11.已知,若,则等于( )
A. B. C. D.1
知识点5:导数运算法则的综合应用
12.已知,为的导函数,则的大致图象是( )
A. B.
C. D.
13.求曲线在点处的切线与x轴、直线所围成的三角形的面积.
二、高考真题
14.(2020.全国卷Ⅰ卷理数)函数的图像在点处的切线方程为( )
A. B.
C. D.
15.(2021.全国卷甲卷理)曲线在点处的切线方程为__________.
三、综合提升
16.已知函数.
(1)求f(x)的解析式;
(2)求f(x)在处的切线方程.
17.已知函数f(x)=x3.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求经过点A(1,f(1))的曲线f(x)的切线方程.
18.在①是三次函数,且,,,,②是二次函数,且这两个条件中任选一个作为已知条件,并回答下列问题.
(1)求函数的解析式;
(2)求的图象在处的切线l与两坐标轴围成的三角形的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
对ABC判断可知,运算正确,对D,,故D错误.
2.A
为常数,则,所以①错误;
y′=,所以②正确;
因为,所以,所以,所以③错误;
,所以④错误.
综上,正确的只有1个.
3.D
∵,
∴,则,
∴.
4.B
y′=′==,
由-a2=0,得x0=±a.
5.A
函数,求导
又,,即
6.A
因为,所以.又曲线在点处的切线方程为,所以,所以,即曲线在点处的切线的斜率为4.
7.D
∵,∴,∴,
∴,∴.
8.B
,
导函数的图象开口向上.
又,
不是偶函数,其图象不关于y轴对称,其图象必为③,
由图象特征知,
且对称轴,
.
故.
9.C
由复合函数求导法则,知函数由基本初等函数,复合而成,
所以.
10.B
∵,∴,
∴.
11.A
因为,所以,
又,所以,因为,所以,所以.
12.A
∵,
∴
易知是奇函数,其图象关于原点对称,故排除B和D,
由,排除C,所以A正确.
13..
设,则,
∴,
∴曲线在点处的切线方程为,即,
∴切线与x轴的交点是,与直线的交点是,
∴所围成的三角形的面积为.
14.B
,,,,
因此,所求切线的方程为,即.
15.
由题,当时,,故点在曲线上.
求导得:,所以.
故切线方程为.
16.(1)
由求导得:,
又,则,解得,
所以的解析式为.
(2)
由(1)得,,则,
在处的切线方程为,即,
所以f(x)在处的切线方程是:.
17.(1) ;(2) 或.
(1)由,得,
故切线斜率,
又因,所以切线方程为,即.
(2)当为切点时,由(1)知,切线方程为;
当不为切点时,设切点,则切线斜率,
故切线方程为,
又因切线过点,所以,解得(舍)或,
因此切线方程为.
综上,过点的切线方程为或.
18.
选①,
(1)依题意,设,则,
由已知得,解得,,,,
所以函数的解析式是;
(2)由(1)知,,,则有切线l的方程为,
当时,,当时,,
所以切线l与两坐标轴围成的三角形的面积.
选②,
(1)依题意,设,则,
于是得:,化简得,
因为上式对任意x都成立,所以,解得,,,
所以函数的解析式为;
(2)由(1)知,,则,又,则有切线l的方程为,
当时,,当时,,
所以切线l与两坐标轴围成的三角形的面积.
答案第1页,共2页
答案第1页,共2页
夯实基础
知识点1:利用导数公式求函数的导数
1.下列求导运算不正确的是( )
A. B.
C. D.
2.给出下列结论:
①=-sin =-;
②若y=,则y′=-2x-3;
③若f(x)=3x,则[ f′(1)]′=3;
④若,则.
其中正确的个数是( )
A.1 B.2 C.3 D.4
知识点2:利用导数的运算法则求导数
3.已知函数,则等于( )
A.0 B.2 C. D.
4.函数y= (a>0)在x=x0处的导数为0,那么x0=( )
A.a B.±a C.-a D.a2
5.已知函数,若,的值为 ( )
A.4 B.5 C.6 D.7
知识点3:导数计算的综合应用
6.设函数,曲线在点处的切线方程为,则曲线在点处的切线的斜率为( )
A.4 B. C.2 D.
7.若,则等于( )
A. B.0 C. D.6
8.下列图象中,有一个是函数(,且)的导函数的图象,则( )
B. C. D.或
知识点4:复合函数的导数
9.下列关于函数的复合过程与导数运算正确的是( )
A.,, B.,,
C.,, D.,,
10.已知函数在上可导,函数,则等于( )
A. B.0 C.1 D.2
11.已知,若,则等于( )
A. B. C. D.1
知识点5:导数运算法则的综合应用
12.已知,为的导函数,则的大致图象是( )
A. B.
C. D.
13.求曲线在点处的切线与x轴、直线所围成的三角形的面积.
二、高考真题
14.(2020.全国卷Ⅰ卷理数)函数的图像在点处的切线方程为( )
A. B.
C. D.
15.(2021.全国卷甲卷理)曲线在点处的切线方程为__________.
三、综合提升
16.已知函数.
(1)求f(x)的解析式;
(2)求f(x)在处的切线方程.
17.已知函数f(x)=x3.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求经过点A(1,f(1))的曲线f(x)的切线方程.
18.在①是三次函数,且,,,,②是二次函数,且这两个条件中任选一个作为已知条件,并回答下列问题.
(1)求函数的解析式;
(2)求的图象在处的切线l与两坐标轴围成的三角形的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
对ABC判断可知,运算正确,对D,,故D错误.
2.A
为常数,则,所以①错误;
y′=,所以②正确;
因为,所以,所以,所以③错误;
,所以④错误.
综上,正确的只有1个.
3.D
∵,
∴,则,
∴.
4.B
y′=′==,
由-a2=0,得x0=±a.
5.A
函数,求导
又,,即
6.A
因为,所以.又曲线在点处的切线方程为,所以,所以,即曲线在点处的切线的斜率为4.
7.D
∵,∴,∴,
∴,∴.
8.B
,
导函数的图象开口向上.
又,
不是偶函数,其图象不关于y轴对称,其图象必为③,
由图象特征知,
且对称轴,
.
故.
9.C
由复合函数求导法则,知函数由基本初等函数,复合而成,
所以.
10.B
∵,∴,
∴.
11.A
因为,所以,
又,所以,因为,所以,所以.
12.A
∵,
∴
易知是奇函数,其图象关于原点对称,故排除B和D,
由,排除C,所以A正确.
13..
设,则,
∴,
∴曲线在点处的切线方程为,即,
∴切线与x轴的交点是,与直线的交点是,
∴所围成的三角形的面积为.
14.B
,,,,
因此,所求切线的方程为,即.
15.
由题,当时,,故点在曲线上.
求导得:,所以.
故切线方程为.
16.(1)
由求导得:,
又,则,解得,
所以的解析式为.
(2)
由(1)得,,则,
在处的切线方程为,即,
所以f(x)在处的切线方程是:.
17.(1) ;(2) 或.
(1)由,得,
故切线斜率,
又因,所以切线方程为,即.
(2)当为切点时,由(1)知,切线方程为;
当不为切点时,设切点,则切线斜率,
故切线方程为,
又因切线过点,所以,解得(舍)或,
因此切线方程为.
综上,过点的切线方程为或.
18.
选①,
(1)依题意,设,则,
由已知得,解得,,,,
所以函数的解析式是;
(2)由(1)知,,,则有切线l的方程为,
当时,,当时,,
所以切线l与两坐标轴围成的三角形的面积.
选②,
(1)依题意,设,则,
于是得:,化简得,
因为上式对任意x都成立,所以,解得,,,
所以函数的解析式为;
(2)由(1)知,,则,又,则有切线l的方程为,
当时,,当时,,
所以切线l与两坐标轴围成的三角形的面积.
答案第1页,共2页
答案第1页,共2页
