2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.1.1 导数的概念及其意义 随堂训练word版含答案
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.1.1 导数的概念及其意义 随堂训练word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 326.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 21:48:52 | ||
图片预览




文档简介
《导数的概念及其意义》随堂训练
夯实基础
知识点1:平均变化率
1.一物体的运动方程是,则t在内的平均速度为( )
A.0.41 B.4.1 C.0.3 D.3
2.函数在区间上的平均变化率等于( ).
A.4 B. C. D.
知识点2:求瞬时速度
3.已知物体做直线运动的方程为,则表示的意义是( )
A.经过4s后物体向前走了10m B.物体在前4秒内的平均速度为10m/s
C.物体在第4秒内向前走了10m D.物体在第4秒末的瞬时速度为10m/s
4.已知物体做自由落体的运动方程为,且无限趋近于0时,无限趋近于9.8m/s.那么关于9.8m/s正确的说法是( ).
A.物体在0~1s这一段时间内的速度
B.物体在这一段时间内的速度
C.物体在1s这一时刻的速度
D.物体从1s到这一段时间内的平均速度
知识点3:导数的概念
5.设在处可导,则( ).
A. B.
C. D.
6.函数在处的导数可表示为,即( ).
A. B.
C. D.
知识点4:求函数在某点处的导数
7.设为可导函数,且当时,,则曲线在点处的切线斜率为( )
A.2 B. C.1 D.
8.函数在处的导数为( )
A.2 B. C. D.
知识点5:导数的几何意义及其应用
9.下面说法正确的是( )
A.若不存在,则曲线在点处没有切线
B.若曲线在点有切线,则必存在
C.若不存在,则曲线在点处的切线斜率不存在
D.若曲线在点处没有切线,则有可能存在
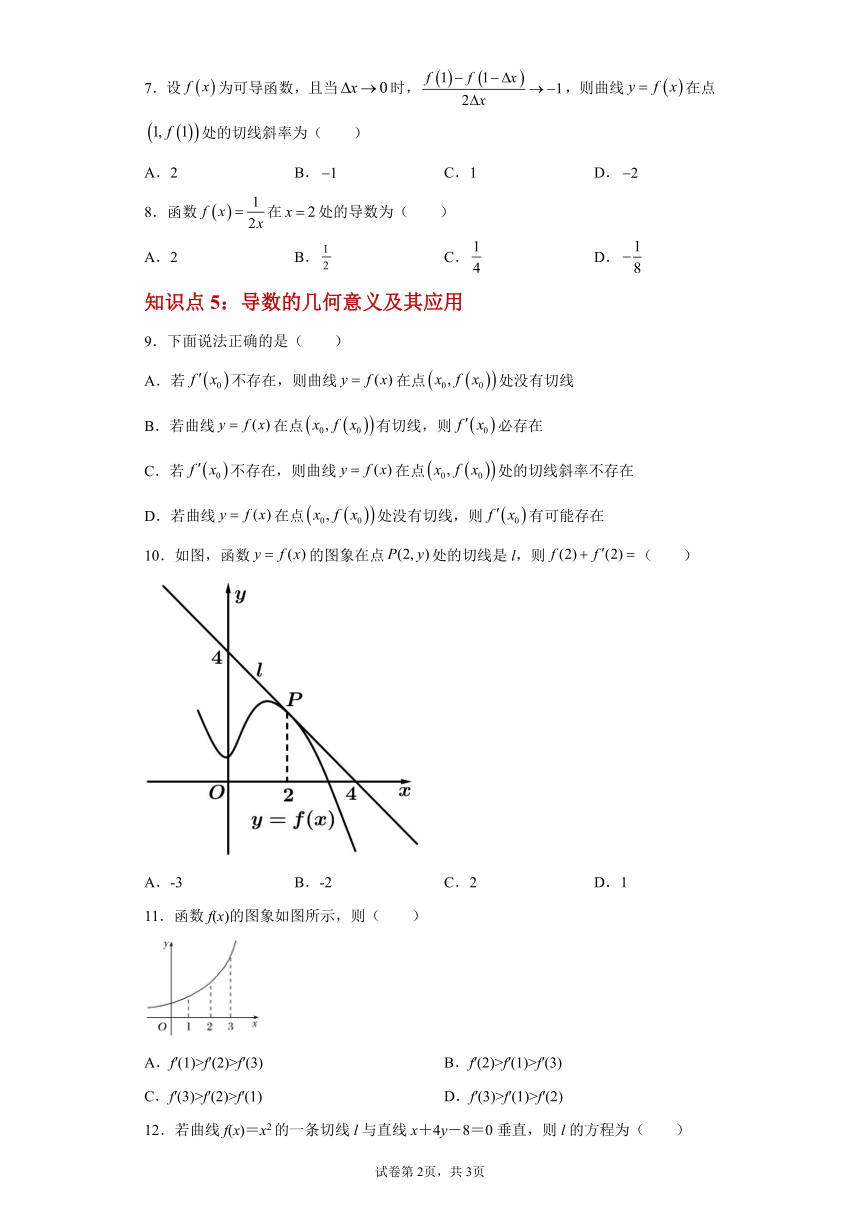
10.如图,函数的图象在点处的切线是l,则( )
A.-3 B.-2 C.2 D.1
11.函数f(x)的图象如图所示,则( )
A.f′(1)>f′(2)>f′(3) B.f′(2)>f′(1)>f′(3)
C.f′(3)>f′(2)>f′(1) D.f′(3)>f′(1)>f′(2)
12.若曲线f(x)=x2的一条切线l与直线x+4y-8=0垂直,则l的方程为( )
A.4x-y-4=0 B.x+4y-5=0
C.4x-y+3=0 D.x+4y+3=0
二、高考真题
13.(2021.全国卷Ⅰ卷)若过点可以作曲线的两条切线,则( )
A. B.
C. D.
14.(2020.高考全国卷Ⅰ卷文数)曲线的一条切线的斜率为2,则该切线的方程为______________.
三、综合提升
15.已知曲线
(1)求曲线S在点A(2,4)处的切线方程;
(2)求过点B(1,—1)并与曲线S相切的直线方程.
16.已知函数,直线l为曲线的切线,且经过原点,求直线l的方程及切点坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
,
2.B
因函数,则在区间上的函数增量有:
,于是有,
所以所求平均变化率等于.
3.D
解:由导数的意义知表示物体在第4秒时的瞬时速度为10m/s.
4.C
由平均速度的概念,表示的是这一段时间内的平均速度,其极限值即,表示这一时刻的瞬时速度.
5.C
解:∵在处可导,
∴,
6.C
是的另一种记法,根据导数的定义可知C正确.
7.D
解:由导数的几何意义,点处的切线斜率为,
因为时,,
所以,
所以在点处的切线斜率为,
8.D
,所以函数在处的导数为.
9.由的几何意义可知,若不存在,则曲线在处切线的斜率不存在,故A错误,C正确;
若曲线在点有切线,该切线斜率不一定存在,所以不一定存在,故B错误;
若曲线在点处没有切线,则一定不存在,故D错误.
如中, ,当时,不存在,但在时的切线方程为,切线斜率不存在.故A、 B错.
10.D
解:由题图可得函数的图象在点P处的切线与x轴交于点,与y轴交于点,则切线,
,,,
11.C
由函数的图象可知,曲线在点A(1,f(1)),B(2,f(2)),C(3,f(3))处切线的斜率大小关系为kC>kB>kA,故f′(3)>f′(2)>f′(1).
12.A
设切点为(x0,y0),
因为=2x.
由题意可知,切线斜率k=4,即=2x0=4,
所以x0=2.所以切点坐标为(2,4),切线方程为y-4=4(x-2),即4x-y-4=0,
D
在曲线上任取一点,对函数求导得,
所以,曲线在点处的切线方程为,即,
由题意可知,点在直线上,可得,
令,则.
当时,,此时函数单调递增,
当时,,此时函数单调递减,
所以,,
由题意可知,直线与曲线的图象有两个交点,则,
当时,,当时,,作出函数的图象如下图所示:
由图可知,当时,直线与曲线的图象有两个交点.
解法二:画出函数曲线的图象如图所示,根据直观即可判定点在曲线下方和轴上方时才可以作出两条切线.由此可知.
14.
设切线的切点坐标为,
,所以切点坐标为,
所求的切线方程为,即.
15.
(1)
∵,则,
∴当时,,
∴点处的切线方程为:,即.
(2)
设为切点,则切线的斜率为,
故切线方程为:,
又知切线过点,代入上述方程,
解得或,
故所求的切线方程为或.
16.
设切点为,
因为
,所以.
当趋于0时,趋于,即,
所以切线方程为,
因为切线过原点,所以,
所以,解得,
所以,故直线l的方程为,又,所以切点的坐标为.答案第1页,共2页
答案第1页,共2页
夯实基础
知识点1:平均变化率
1.一物体的运动方程是,则t在内的平均速度为( )
A.0.41 B.4.1 C.0.3 D.3
2.函数在区间上的平均变化率等于( ).
A.4 B. C. D.
知识点2:求瞬时速度
3.已知物体做直线运动的方程为,则表示的意义是( )
A.经过4s后物体向前走了10m B.物体在前4秒内的平均速度为10m/s
C.物体在第4秒内向前走了10m D.物体在第4秒末的瞬时速度为10m/s
4.已知物体做自由落体的运动方程为,且无限趋近于0时,无限趋近于9.8m/s.那么关于9.8m/s正确的说法是( ).
A.物体在0~1s这一段时间内的速度
B.物体在这一段时间内的速度
C.物体在1s这一时刻的速度
D.物体从1s到这一段时间内的平均速度
知识点3:导数的概念
5.设在处可导,则( ).
A. B.
C. D.
6.函数在处的导数可表示为,即( ).
A. B.
C. D.
知识点4:求函数在某点处的导数
7.设为可导函数,且当时,,则曲线在点处的切线斜率为( )
A.2 B. C.1 D.
8.函数在处的导数为( )
A.2 B. C. D.
知识点5:导数的几何意义及其应用
9.下面说法正确的是( )
A.若不存在,则曲线在点处没有切线
B.若曲线在点有切线,则必存在
C.若不存在,则曲线在点处的切线斜率不存在
D.若曲线在点处没有切线,则有可能存在
10.如图,函数的图象在点处的切线是l,则( )
A.-3 B.-2 C.2 D.1
11.函数f(x)的图象如图所示,则( )
A.f′(1)>f′(2)>f′(3) B.f′(2)>f′(1)>f′(3)
C.f′(3)>f′(2)>f′(1) D.f′(3)>f′(1)>f′(2)
12.若曲线f(x)=x2的一条切线l与直线x+4y-8=0垂直,则l的方程为( )
A.4x-y-4=0 B.x+4y-5=0
C.4x-y+3=0 D.x+4y+3=0
二、高考真题
13.(2021.全国卷Ⅰ卷)若过点可以作曲线的两条切线,则( )
A. B.
C. D.
14.(2020.高考全国卷Ⅰ卷文数)曲线的一条切线的斜率为2,则该切线的方程为______________.
三、综合提升
15.已知曲线
(1)求曲线S在点A(2,4)处的切线方程;
(2)求过点B(1,—1)并与曲线S相切的直线方程.
16.已知函数,直线l为曲线的切线,且经过原点,求直线l的方程及切点坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
,
2.B
因函数,则在区间上的函数增量有:
,于是有,
所以所求平均变化率等于.
3.D
解:由导数的意义知表示物体在第4秒时的瞬时速度为10m/s.
4.C
由平均速度的概念,表示的是这一段时间内的平均速度,其极限值即,表示这一时刻的瞬时速度.
5.C
解:∵在处可导,
∴,
6.C
是的另一种记法,根据导数的定义可知C正确.
7.D
解:由导数的几何意义,点处的切线斜率为,
因为时,,
所以,
所以在点处的切线斜率为,
8.D
,所以函数在处的导数为.
9.由的几何意义可知,若不存在,则曲线在处切线的斜率不存在,故A错误,C正确;
若曲线在点有切线,该切线斜率不一定存在,所以不一定存在,故B错误;
若曲线在点处没有切线,则一定不存在,故D错误.
如中, ,当时,不存在,但在时的切线方程为,切线斜率不存在.故A、 B错.
10.D
解:由题图可得函数的图象在点P处的切线与x轴交于点,与y轴交于点,则切线,
,,,
11.C
由函数的图象可知,曲线在点A(1,f(1)),B(2,f(2)),C(3,f(3))处切线的斜率大小关系为kC>kB>kA,故f′(3)>f′(2)>f′(1).
12.A
设切点为(x0,y0),
因为=2x.
由题意可知,切线斜率k=4,即=2x0=4,
所以x0=2.所以切点坐标为(2,4),切线方程为y-4=4(x-2),即4x-y-4=0,
D
在曲线上任取一点,对函数求导得,
所以,曲线在点处的切线方程为,即,
由题意可知,点在直线上,可得,
令,则.
当时,,此时函数单调递增,
当时,,此时函数单调递减,
所以,,
由题意可知,直线与曲线的图象有两个交点,则,
当时,,当时,,作出函数的图象如下图所示:
由图可知,当时,直线与曲线的图象有两个交点.
解法二:画出函数曲线的图象如图所示,根据直观即可判定点在曲线下方和轴上方时才可以作出两条切线.由此可知.
14.
设切线的切点坐标为,
,所以切点坐标为,
所求的切线方程为,即.
15.
(1)
∵,则,
∴当时,,
∴点处的切线方程为:,即.
(2)
设为切点,则切线的斜率为,
故切线方程为:,
又知切线过点,代入上述方程,
解得或,
故所求的切线方程为或.
16.
设切点为,
因为
,所以.
当趋于0时,趋于,即,
所以切线方程为,
因为切线过原点,所以,
所以,解得,
所以,故直线l的方程为,又,所以切点的坐标为.答案第1页,共2页
答案第1页,共2页
