人教版八年级数学上册12.2《全等三角形 角边角和角角边判定》教案
文档属性
| 名称 | 人教版八年级数学上册12.2《全等三角形 角边角和角角边判定》教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 309.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 00:00:00 | ||
图片预览



文档简介
《全等三角形角边角和角角边判定》教案
教学内容
本节课主要内容是探索三角形全等(ASA,AAS),及利用它进行三角形全等的证明。
教学目标
知识与技能
理解"角边角"、"角角边"判定三角形全等的方法
过程与方法
经历探索理解"角边角"、"角角边"判定三角形全等的过程,能运用已学过的三角形全等的判定方法解决实际问题
情感、态度与价值观
培养良好的几何推理意识,发展思维,感悟全等三角形的应用价值
重点难点
重点:应用"角边角"、"角角边"判定三角形全等
难点:学会利用综合法解决几何推理问题
关键:把握综合分析法的思想,寻找问题的切入点
教学方法
采用问题教学法,在情景问题中激发学生的求知欲
教学过程
一回顾交流,巩固学习(投影展示)
1.什么样的图形是全等三角形?
答:能够重合的三角形是全等三角形
2.判断三角形全等至少要有几个条件?
答:至少要有三个条件
3.学过的判断三角形全等的方法有哪些?
边边边(SSS)公理:
有三边对应相等的两个三角形全等。
边角边(SAS)公理:
有两边和它们夹角对应相等的两个三角形全等。
二实践操作,导入新课
问题
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
答:角边角(ASA) 角角边(AAS)
探究 角边角(ASA)
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B (即使两角和它们的夹边对应相等)。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
已知:任意 △ ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B :
画法:
(1)画A/B/=AB;
(2)在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/。
△A/B/C/就是所要画的三角形。
规律 两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角” 或“ASA”)。
用数学符号表示:
在△ABE和△A’CD中
∠A=∠A’ (已知 )
AB=A’C(已知 )
∠B=∠C(已知 )
4.填空
如图,应填什么就有 △AOC≌ △BOD:
∠A=∠B,(已知)
, ,
∠1=∠2, (已知)
∴△AOC≌△BOD (ASA)
三范例点击,应用所学
1理清思路
三角形全等的三种条件
(1)直接条件:要全等的三角形的边或角(全等时直接用)
(2)间接条件:和要全等的三角形的边或角有关的条件(要先转换成直接条件)
(3)隐含条件:公共边,公共角,对顶角等(全等时直接用)
证明三角形全等的过程
(1)把间接条件转换为直接条件(有几个转换几个)
(2)把全等的三个条件列出来证明全等
(3)由全等推出边或角相等
(4)再推其他相关的内容
2.例题讲解
例1已知:点D在AB上,点E在AC上,
BE和CD相交于点O,
AB=AC,∠B=∠C。
求证:(1)AD=AE; (2)BD=CE。
3.简单应用
(1)如图,O是AB的中点,∠A= ∠B,
△AOC与△BOD全等吗 为什么?
(2)如图,点B、E、C、F在一条直线上,
AB=DE,AB∥DE,∠A=∠D.
求证:BE=CF.
4.实际应用
小明踢球时不慎把一块三角形玻璃
打碎为两块,他是否可以只带其中的
一块碎片到商店去,就能配一块于原
来一样的三角形玻璃呢 如果可以,
带哪块去合适呢 为什么
四.探究角角边(AAS)
1.如下图,在△ABC和△DEF中,∠A =∠D, ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
2.规律
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。
用数学符号表示:
在△ABE和△A’CD中
AE=A’D(已知 )
∠A=∠A’ (已知 )
∠B=∠C(已知 )
∴ △ABE≌△A’CD(AAS)
3.简单应用
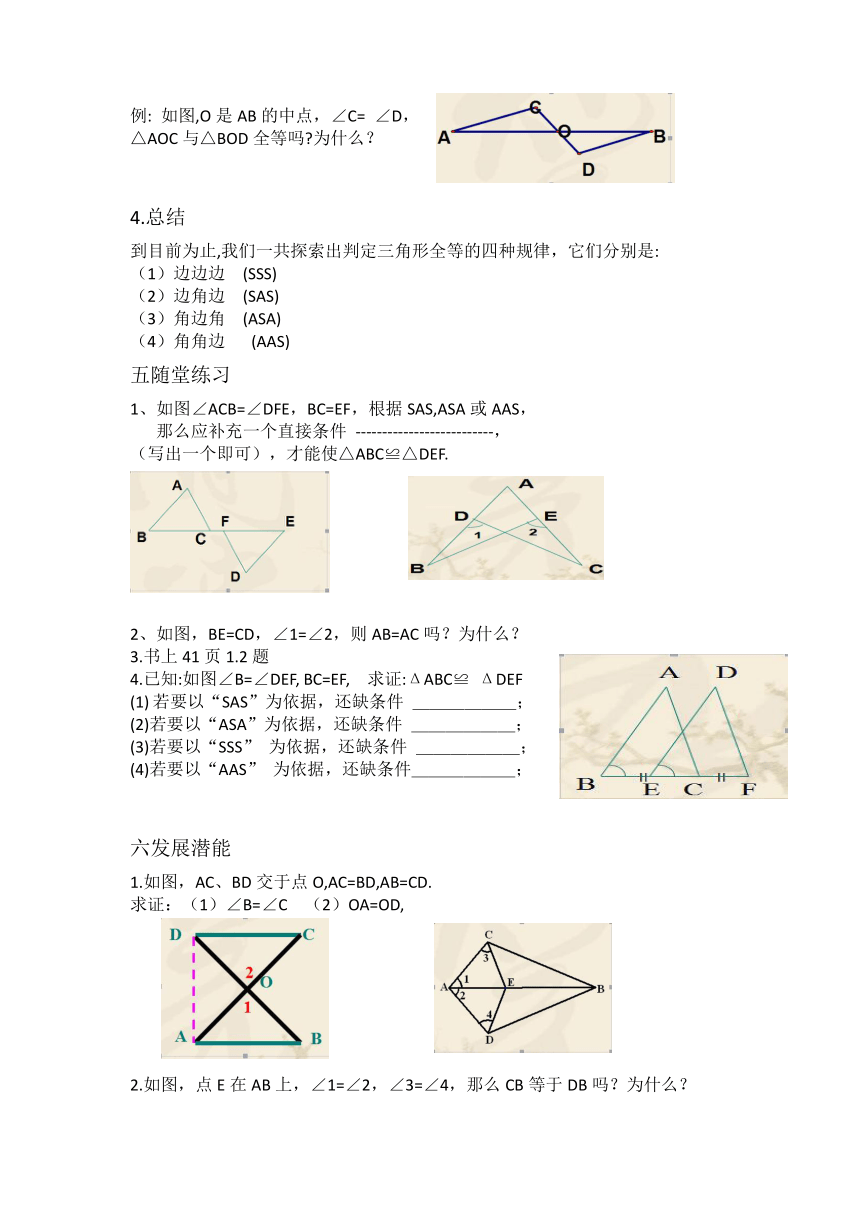
例: 如图,O是AB的中点,∠C= ∠D,
△AOC与△BOD全等吗 为什么?
4.总结
到目前为止,我们一共探索出判定三角形全等的四种规律,它们分别是:
(1)边边边 (SSS)
(2)边角边 (SAS)
(3)角边角 (ASA)
(4)角角边 (AAS)
五随堂练习
1、如图∠ACB=∠DFE,BC=EF,根据SAS,ASA或AAS,
那么应补充一个直接条件 --------------------------,
(写出一个即可),才能使△ABC≌△DEF.
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
3.书上41页1.2题
4.已知:如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
若要以“SAS”为依据,还缺条件 ______;
(2)若要以“ASA”为依据,还缺条件 ______;
(3)若要以“SSS” 为依据,还缺条件 ______;
(4)若要以“AAS” 为依据,还缺条件______;
六发展潜能
1.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:(1)∠B=∠C (2)OA=OD,
2.如图,点E在AB上,∠1=∠2,∠3=∠4,那么CB等于DB吗?为什么?
3.如图,AB∥DC,AD∥BC,说出△ABD≌ △CDB的理由。
4.如图,AB=DE,AF=CD,EF=BC,∠A=∠D,试说明:BF∥CE
5. 已知:如图, △AEF 与△ABC中, ∠E =∠B, EF=BC.请你添加一个条件,使△AEF ≌ △ABC.
6.如图,在△ABC和△BAD中,BC = AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 .
7.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(1)当直线MN旋转到如图(1)所示的位置时,猜想线段AD、BE、DE的数量关系,并证明你的猜想。
(2)当直线MN旋转到图(2)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
(3)当直线MN旋转到图(3)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
七布置作业
书上44页第9、10题 、
全等三角形的判定习题课
教学内容
本节课主要内容是复习判定三角形全等的几种方法,及利用它进行三角形全等的证明。
教学目标:
1、通过全等三角形的概念和识别方法的复习,让学生体会辨别、探寻、运用全等三角形的一般方法,体会主动实验,探究新知的方法。
2、培养学生观察和理解能力,几何语言的叙述能力及运用全等知识解决实际问题的能力。
3、在学生操作过程中,激发学生学习的兴趣,培养学生主动探索,敢于实践的精神,培养学生之间合作交流的习惯。
教学的重点和难点:
重点:运用全等三角形的识别方法来探寻三角形以及运用全等三角形
的知识解决实际问题。
难点:运用全等三角形知识来解决实际问题。
教学过程设计:
一判定三角形全等的方法总结
到目前为止,我们一共探索出判定三角形全等的四种规律,它们分别是:
(1)边边边 (SSS)
(2)边角边 (SAS)
(3)角边角 (ASA)
(4)角角边 (AAS)
二小试牛刀
1、如图∠ACB=∠DFE,BC=EF,根据SAS,ASA或AAS,
那么应补充一个直接条件 --------------------------,
(写出一个即可),才能使△ABC≌△DEF.
2.如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
3.书上41页1.2题
4.已知:如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
若要以“SAS”为依据,还缺条件 ______;
(2)若要以“ASA”为依据,还缺条件 ______;
(3)若要以“SSS” 为依据,还缺条件 ______;
(4)若要以“AAS” 为依据,还缺条件______;
三发展潜能
1.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:(1)∠B=∠C (2)OA=OD,
2.如图,点E在AB上,∠1=∠2,∠3=∠4,那么CB等于DB吗?为什么?
3.如图,AB∥DC,AD∥BC,说出△ABD≌ △CDB的理由。
4.如图,AB=DE,AF=CD,EF=BC,∠A=∠D,试说明:BF∥CE
5. 已知:如图, △AEF 与△ABC中, ∠E =∠B, EF=BC.请你添加一个条件,使△AEF ≌ △ABC.
6.如图,在△ABC和△BAD中,BC = AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 .
7.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(1)当直线MN旋转到如图(1)所示的位置时,猜想线段AD、BE、DE的数量关系,并证明你的猜想。
(2)当直线MN旋转到图(2)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
(3)当直线MN旋转到图(3)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
七布置作业
书上44页第11、12题 、
教学内容
本节课主要内容是探索三角形全等(ASA,AAS),及利用它进行三角形全等的证明。
教学目标
知识与技能
理解"角边角"、"角角边"判定三角形全等的方法
过程与方法
经历探索理解"角边角"、"角角边"判定三角形全等的过程,能运用已学过的三角形全等的判定方法解决实际问题
情感、态度与价值观
培养良好的几何推理意识,发展思维,感悟全等三角形的应用价值
重点难点
重点:应用"角边角"、"角角边"判定三角形全等
难点:学会利用综合法解决几何推理问题
关键:把握综合分析法的思想,寻找问题的切入点
教学方法
采用问题教学法,在情景问题中激发学生的求知欲
教学过程
一回顾交流,巩固学习(投影展示)
1.什么样的图形是全等三角形?
答:能够重合的三角形是全等三角形
2.判断三角形全等至少要有几个条件?
答:至少要有三个条件
3.学过的判断三角形全等的方法有哪些?
边边边(SSS)公理:
有三边对应相等的两个三角形全等。
边角边(SAS)公理:
有两边和它们夹角对应相等的两个三角形全等。
二实践操作,导入新课
问题
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
答:角边角(ASA) 角角边(AAS)
探究 角边角(ASA)
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B (即使两角和它们的夹边对应相等)。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
已知:任意 △ ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B :
画法:
(1)画A/B/=AB;
(2)在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/。
△A/B/C/就是所要画的三角形。
规律 两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角” 或“ASA”)。
用数学符号表示:
在△ABE和△A’CD中
∠A=∠A’ (已知 )
AB=A’C(已知 )
∠B=∠C(已知 )
4.填空
如图,应填什么就有 △AOC≌ △BOD:
∠A=∠B,(已知)
, ,
∠1=∠2, (已知)
∴△AOC≌△BOD (ASA)
三范例点击,应用所学
1理清思路
三角形全等的三种条件
(1)直接条件:要全等的三角形的边或角(全等时直接用)
(2)间接条件:和要全等的三角形的边或角有关的条件(要先转换成直接条件)
(3)隐含条件:公共边,公共角,对顶角等(全等时直接用)
证明三角形全等的过程
(1)把间接条件转换为直接条件(有几个转换几个)
(2)把全等的三个条件列出来证明全等
(3)由全等推出边或角相等
(4)再推其他相关的内容
2.例题讲解
例1已知:点D在AB上,点E在AC上,
BE和CD相交于点O,
AB=AC,∠B=∠C。
求证:(1)AD=AE; (2)BD=CE。
3.简单应用
(1)如图,O是AB的中点,∠A= ∠B,
△AOC与△BOD全等吗 为什么?
(2)如图,点B、E、C、F在一条直线上,
AB=DE,AB∥DE,∠A=∠D.
求证:BE=CF.
4.实际应用
小明踢球时不慎把一块三角形玻璃
打碎为两块,他是否可以只带其中的
一块碎片到商店去,就能配一块于原
来一样的三角形玻璃呢 如果可以,
带哪块去合适呢 为什么
四.探究角角边(AAS)
1.如下图,在△ABC和△DEF中,∠A =∠D, ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
2.规律
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。
用数学符号表示:
在△ABE和△A’CD中
AE=A’D(已知 )
∠A=∠A’ (已知 )
∠B=∠C(已知 )
∴ △ABE≌△A’CD(AAS)
3.简单应用
例: 如图,O是AB的中点,∠C= ∠D,
△AOC与△BOD全等吗 为什么?
4.总结
到目前为止,我们一共探索出判定三角形全等的四种规律,它们分别是:
(1)边边边 (SSS)
(2)边角边 (SAS)
(3)角边角 (ASA)
(4)角角边 (AAS)
五随堂练习
1、如图∠ACB=∠DFE,BC=EF,根据SAS,ASA或AAS,
那么应补充一个直接条件 --------------------------,
(写出一个即可),才能使△ABC≌△DEF.
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
3.书上41页1.2题
4.已知:如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
若要以“SAS”为依据,还缺条件 ______;
(2)若要以“ASA”为依据,还缺条件 ______;
(3)若要以“SSS” 为依据,还缺条件 ______;
(4)若要以“AAS” 为依据,还缺条件______;
六发展潜能
1.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:(1)∠B=∠C (2)OA=OD,
2.如图,点E在AB上,∠1=∠2,∠3=∠4,那么CB等于DB吗?为什么?
3.如图,AB∥DC,AD∥BC,说出△ABD≌ △CDB的理由。
4.如图,AB=DE,AF=CD,EF=BC,∠A=∠D,试说明:BF∥CE
5. 已知:如图, △AEF 与△ABC中, ∠E =∠B, EF=BC.请你添加一个条件,使△AEF ≌ △ABC.
6.如图,在△ABC和△BAD中,BC = AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 .
7.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(1)当直线MN旋转到如图(1)所示的位置时,猜想线段AD、BE、DE的数量关系,并证明你的猜想。
(2)当直线MN旋转到图(2)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
(3)当直线MN旋转到图(3)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
七布置作业
书上44页第9、10题 、
全等三角形的判定习题课
教学内容
本节课主要内容是复习判定三角形全等的几种方法,及利用它进行三角形全等的证明。
教学目标:
1、通过全等三角形的概念和识别方法的复习,让学生体会辨别、探寻、运用全等三角形的一般方法,体会主动实验,探究新知的方法。
2、培养学生观察和理解能力,几何语言的叙述能力及运用全等知识解决实际问题的能力。
3、在学生操作过程中,激发学生学习的兴趣,培养学生主动探索,敢于实践的精神,培养学生之间合作交流的习惯。
教学的重点和难点:
重点:运用全等三角形的识别方法来探寻三角形以及运用全等三角形
的知识解决实际问题。
难点:运用全等三角形知识来解决实际问题。
教学过程设计:
一判定三角形全等的方法总结
到目前为止,我们一共探索出判定三角形全等的四种规律,它们分别是:
(1)边边边 (SSS)
(2)边角边 (SAS)
(3)角边角 (ASA)
(4)角角边 (AAS)
二小试牛刀
1、如图∠ACB=∠DFE,BC=EF,根据SAS,ASA或AAS,
那么应补充一个直接条件 --------------------------,
(写出一个即可),才能使△ABC≌△DEF.
2.如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
3.书上41页1.2题
4.已知:如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
若要以“SAS”为依据,还缺条件 ______;
(2)若要以“ASA”为依据,还缺条件 ______;
(3)若要以“SSS” 为依据,还缺条件 ______;
(4)若要以“AAS” 为依据,还缺条件______;
三发展潜能
1.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:(1)∠B=∠C (2)OA=OD,
2.如图,点E在AB上,∠1=∠2,∠3=∠4,那么CB等于DB吗?为什么?
3.如图,AB∥DC,AD∥BC,说出△ABD≌ △CDB的理由。
4.如图,AB=DE,AF=CD,EF=BC,∠A=∠D,试说明:BF∥CE
5. 已知:如图, △AEF 与△ABC中, ∠E =∠B, EF=BC.请你添加一个条件,使△AEF ≌ △ABC.
6.如图,在△ABC和△BAD中,BC = AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 .
7.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(1)当直线MN旋转到如图(1)所示的位置时,猜想线段AD、BE、DE的数量关系,并证明你的猜想。
(2)当直线MN旋转到图(2)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
(3)当直线MN旋转到图(3)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
七布置作业
书上44页第11、12题 、
