人教版八年级数学上册12.2《全等三角形 角边角和角角边判定》教学课件(共26张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.2《全等三角形 角边角和角角边判定》教学课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 395.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 07:35:31 | ||
图片预览







文档简介
(共26张PPT)
三角形全等的判定(ASA,AAS)
回首往事:
1.判断三角形全等至少要有几个条件?
答:至少要有三个条件
边边边(SSS)公理:
有三边对应相等的两个三角形全等。
边角边(SAS)公理:
有两边和它们夹角对应相等的两个三角形全等。
2.学过的判断三角形全等的方法有哪些?
三角形全等的三种条件
1.直接条件:要全等的三角形的边或角(全等时直接用)
2.间接条件:和要全等的三角形的边或角有关的条件(要先转换成直接 条件)
3.隐含条件:公共边,公共角,对顶角等(全等时直接用)
证明三角形全等的过程
1.把间接条件转换为直接条件(有几个转换几个)
2.把全等的三个条件列出来证明全等
3.由全等推出边或角相等
4.再推其他相关的内容
A
B
C
A
B
C
问题:
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
答:角边角(ASA) 角角边(AAS)
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B (即使两角和它们的夹边对应相等)。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
探究5
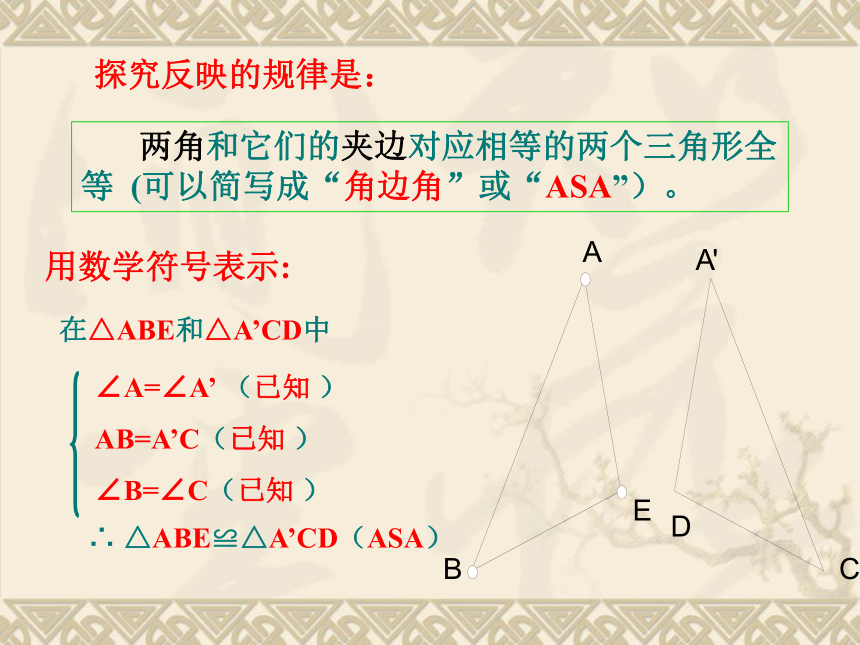
∠A=∠A’ (已知 )
AB=A’C(已知 )
∠B=∠C(已知 )
在△ABE和△A’CD中
∴ △ABE≌△A’CD(ASA)
用数学符号表示:
两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角”或“ASA”)。
探究反映的规律是:
如图,应填什么就有 △AOC≌ △BOD:
∠A=∠B,(已知)
,
∠1=∠2, (已知)
∴△AOC≌△BOD (ASA)
AO=BO
两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角”或“ASA”)。
1
2
例题讲解
例1.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C。
求证:(1)AD=AE; (2)BD=CE。
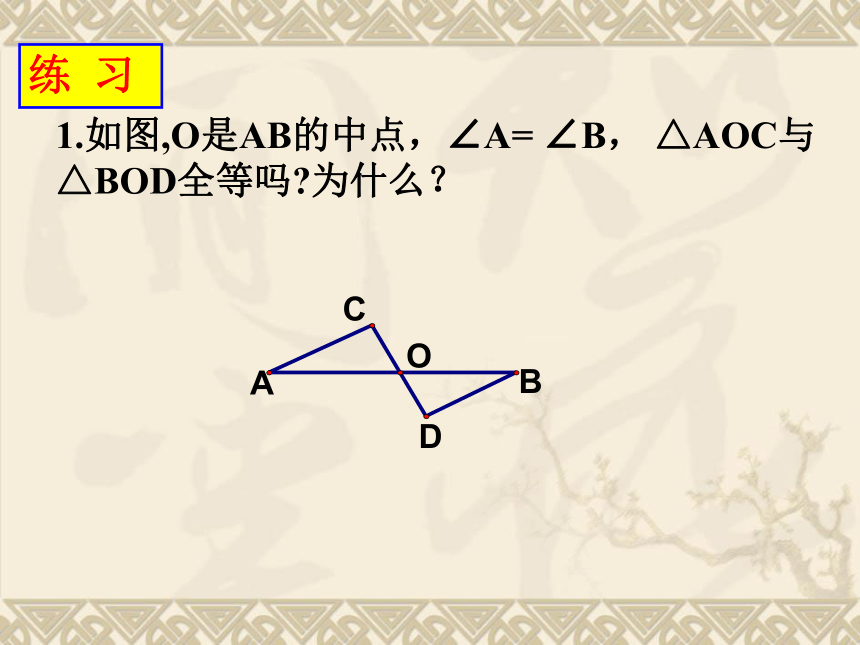
1.如图,O是AB的中点,∠A= ∠B, △AOC与△BOD全等吗 为什么?
O
A
B
C
D
练 习
2. 如图,点B、E、C、F在一条直线上,AB=DE,AB∥DE,∠A=∠D.
求证:BE=CF.
帮帮我
小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢
如果可以,带哪块去合适呢 为什么
(2)
(1)
C
利用“角边角”可知,带第(2)块去,
可以配到一个与原来全等的三角形玻璃。
(1)
(2)
B
E
A
D
(2)
探究6
如下图,在△ABC和△DEF中,∠A =∠D, ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
E
F
D
B
A
C
在△ABC和△DEF中,
∠A +∠B +∠C=1800,
∠D +∠E +∠F =1800,
∵ ∠A =∠D, ∠B=∠E,
∴ ∠C=∠F,
∴ ∠B=∠E,
BC=EF,
∠C=∠F,
∴ △ABC ≌△DEF (ASA)
∠A=∠A’ (已知 )
∠B=∠C(已知 )
AE=A’D(已知 )
在△ABE和△A’CD中
∴ △ABE≌△A’CD(AAS)
用数学符号表示:
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。
探究反映的规律是:
到目前为止,我们一共探索出判定三角形全等的四种规律,它们分别是:
1、边边边 (SSS)
3、角边角 (ASA)
4、角角边 (AAS)
2、边角边 (SAS)
练 习
=
=
A
B
E
C
F
D
已知:
如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
(1)若要以“SAS”为依据,还缺条件 ______; (2)若要以“ASA”为依据,还缺条件 ;
(3)若要以“SSS” 为依据,还缺条件 ;
(4)若要以“AAS” 为依据,还缺条件______;
∠ACB= ∠DEF
AB=DE
AB=DE、AC=DF
∠A= ∠D
知识应用
1. 如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A, C,E在一条直线上,
这时测得DE的长就是AB的长。为什么?
A
B
C
D
E
F
1
2
2.如图,AB⊥BC, AD⊥DC, ∠1=∠2.
求证: AB=AD.
在△ABC和△ADC中,
∠B=∠D,
∠1=∠2,
AC=AC,
∴ △ABC ≌△ADC (AAS)
∴ AB=AD.
证明: ∵ AB⊥BC, AD⊥DC,
∴ ∠B=∠D=900,
∴△BDE≌△CDF (AAS)
∟
∟
4.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:
A
B
C
D
O
证明: (1)连接AD, 在△ADC和△DAB中
AD=DA(公共边)
AC=DB(已知)
DC=AB(已知)
∴△ADC≌△DAB (SSS)
∴∠C=∠B(全等三角形的对应角相等)
(2) 在△ AOB 和△ DOC中
∠ B =∠ C (已证)
∠1=∠2 (对顶角相等)
DC=AB(已知)
∴△DOC≌△AOB (AAS)
∴OA=OD
(全等三角形的对应边相等)
1
2
综合应用
1.如图,点E在AB上,∠1=∠2,∠3=∠4,那么CB等于DB吗?为什么?
-----全等三角形判定
2. 如图,AB=DE,AF=CD,EF=BC,∠A=∠D,
试说明:BF∥CE
A
B
C
D
E
F
3.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(1)当直线MN旋转到如图(1)所示的位置时,猜想线段AD、BE、DE的数量关系,并证明你的猜想。
图(1)
3.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(2)当直线MN旋转到图(2)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
图(2)
3.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(3)当直线MN旋转到图(3)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
图(3)
作业
书上44页第4.5.11题
三角形全等的判定(ASA,AAS)
回首往事:
1.判断三角形全等至少要有几个条件?
答:至少要有三个条件
边边边(SSS)公理:
有三边对应相等的两个三角形全等。
边角边(SAS)公理:
有两边和它们夹角对应相等的两个三角形全等。
2.学过的判断三角形全等的方法有哪些?
三角形全等的三种条件
1.直接条件:要全等的三角形的边或角(全等时直接用)
2.间接条件:和要全等的三角形的边或角有关的条件(要先转换成直接 条件)
3.隐含条件:公共边,公共角,对顶角等(全等时直接用)
证明三角形全等的过程
1.把间接条件转换为直接条件(有几个转换几个)
2.把全等的三个条件列出来证明全等
3.由全等推出边或角相等
4.再推其他相关的内容
A
B
C
A
B
C
问题:
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
答:角边角(ASA) 角角边(AAS)
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B (即使两角和它们的夹边对应相等)。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
探究5
∠A=∠A’ (已知 )
AB=A’C(已知 )
∠B=∠C(已知 )
在△ABE和△A’CD中
∴ △ABE≌△A’CD(ASA)
用数学符号表示:
两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角”或“ASA”)。
探究反映的规律是:
如图,应填什么就有 △AOC≌ △BOD:
∠A=∠B,(已知)
,
∠1=∠2, (已知)
∴△AOC≌△BOD (ASA)
AO=BO
两角和它们的夹边对应相等的两个三角形全等 (可以简写成“角边角”或“ASA”)。
1
2
例题讲解
例1.已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C。
求证:(1)AD=AE; (2)BD=CE。
1.如图,O是AB的中点,∠A= ∠B, △AOC与△BOD全等吗 为什么?
O
A
B
C
D
练 习
2. 如图,点B、E、C、F在一条直线上,AB=DE,AB∥DE,∠A=∠D.
求证:BE=CF.
帮帮我
小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢
如果可以,带哪块去合适呢 为什么
(2)
(1)
C
利用“角边角”可知,带第(2)块去,
可以配到一个与原来全等的三角形玻璃。
(1)
(2)
B
E
A
D
(2)
探究6
如下图,在△ABC和△DEF中,∠A =∠D, ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
E
F
D
B
A
C
在△ABC和△DEF中,
∠A +∠B +∠C=1800,
∠D +∠E +∠F =1800,
∵ ∠A =∠D, ∠B=∠E,
∴ ∠C=∠F,
∴ ∠B=∠E,
BC=EF,
∠C=∠F,
∴ △ABC ≌△DEF (ASA)
∠A=∠A’ (已知 )
∠B=∠C(已知 )
AE=A’D(已知 )
在△ABE和△A’CD中
∴ △ABE≌△A’CD(AAS)
用数学符号表示:
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)。
探究反映的规律是:
到目前为止,我们一共探索出判定三角形全等的四种规律,它们分别是:
1、边边边 (SSS)
3、角边角 (ASA)
4、角角边 (AAS)
2、边角边 (SAS)
练 习
=
=
A
B
E
C
F
D
已知:
如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
(1)若要以“SAS”为依据,还缺条件 ______; (2)若要以“ASA”为依据,还缺条件 ;
(3)若要以“SSS” 为依据,还缺条件 ;
(4)若要以“AAS” 为依据,还缺条件______;
∠ACB= ∠DEF
AB=DE
AB=DE、AC=DF
∠A= ∠D
知识应用
1. 如图,要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A, C,E在一条直线上,
这时测得DE的长就是AB的长。为什么?
A
B
C
D
E
F
1
2
2.如图,AB⊥BC, AD⊥DC, ∠1=∠2.
求证: AB=AD.
在△ABC和△ADC中,
∠B=∠D,
∠1=∠2,
AC=AC,
∴ △ABC ≌△ADC (AAS)
∴ AB=AD.
证明: ∵ AB⊥BC, AD⊥DC,
∴ ∠B=∠D=900,
∴△BDE≌△CDF (AAS)
∟
∟
4.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:
A
B
C
D
O
证明: (1)连接AD, 在△ADC和△DAB中
AD=DA(公共边)
AC=DB(已知)
DC=AB(已知)
∴△ADC≌△DAB (SSS)
∴∠C=∠B(全等三角形的对应角相等)
(2) 在△ AOB 和△ DOC中
∠ B =∠ C (已证)
∠1=∠2 (对顶角相等)
DC=AB(已知)
∴△DOC≌△AOB (AAS)
∴OA=OD
(全等三角形的对应边相等)
1
2
综合应用
1.如图,点E在AB上,∠1=∠2,∠3=∠4,那么CB等于DB吗?为什么?
-----全等三角形判定
2. 如图,AB=DE,AF=CD,EF=BC,∠A=∠D,
试说明:BF∥CE
A
B
C
D
E
F
3.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(1)当直线MN旋转到如图(1)所示的位置时,猜想线段AD、BE、DE的数量关系,并证明你的猜想。
图(1)
3.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(2)当直线MN旋转到图(2)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
图(2)
3.在△ABC中, ∠ACB=90°,AC=BC,直线MN经过点C, AD⊥MN于点D, BE ⊥MN于点E,
(3)当直线MN旋转到图(3)的位置时,猜想线段AD,BE,DE的数量关系,并证明你的猜想
图(3)
作业
书上44页第4.5.11题
