5.2.1求解二元一次方程组(1)课件(共20张PPT)
文档属性
| 名称 | 5.2.1求解二元一次方程组(1)课件(共20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 601.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
5.2.1求解二元一次方程组(1)
第五章
二元一次方程组
2021-2022学年八年级数学上册同步(北师版)
学习目标
1.掌握代入消元法解二元一次方程组的步骤。
2.了解解二元一次方程组的基本思路。
3.初步体会化归思想在数学学习中的运用。
导入新课
2.什么是二元一次方程组?
1.什么是二元一次方程
3.什么是二元一次方程组的解?
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
二元一次方程组中各个方程的公共解,叫做二元一次方程组的解.
导入新课
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
(1)如果设胜的场数是x
,则负的场数是10-x,
可得一元一次方程
;
(2)如果设胜的场数是x
,负的场数是y,
可得二元一次方程组
那么怎样解这个二元一次方程组呢?
讲授新课
用代入法解二元一次方程组
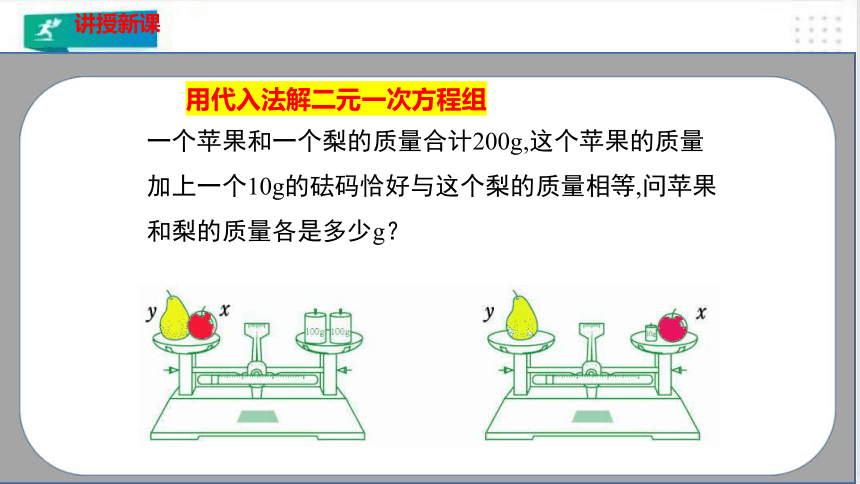
一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
讲授新课
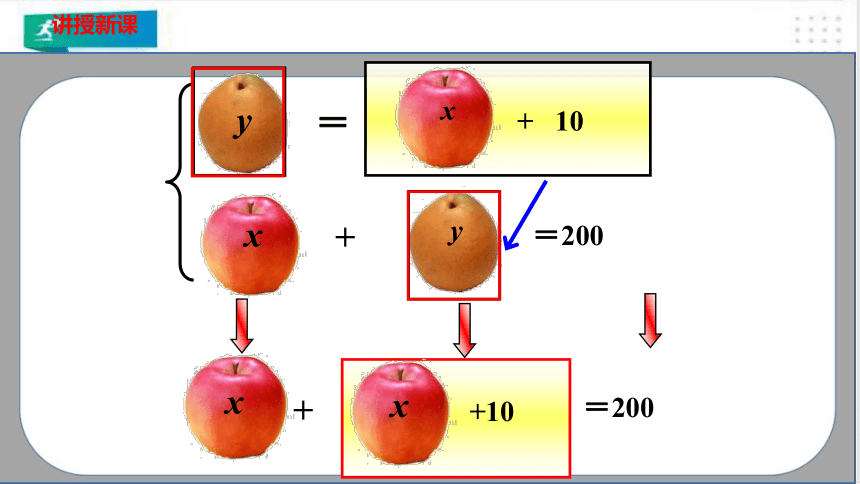
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
讲授新课
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
要点归纳
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
讲授新课
将y=1代入② ,得 x=4.
经检验, x=4,y=1适合原方程组.
所以原方程组的解是
x=5,
y=2.
解:将②代入①,得 3(y+3)+2y=14
3y +9+2y =14
5y=5
y=1.
例1:解方程组
3x+2y=14 ①
x=y+3 ②
检验可以口算或在草稿纸上验算,以后可以不必写出.
讲授新课
将y=2代入③ ,得 x=5.
所以原方程组的解是
x=5,
y=2.
解:由②,得 x=13-4y ③
将③代入①,得 2(13 - 4y)+3y=16
26 –8y +3y =16
-5y=-10
y=2
例2:解方程组
2x+3y=16 ①
x+4y=13 ②
归纳总结
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的另一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
当堂检测
1.二元一次方程组 的解是( )
D
A.
C.
B.
D.
当堂检测
D
2.已知方程组 用代入法消去y后的方程是( )
A.x+x-1=3
B.x+2x-1=3
C.x+x-2=3
D.x+2(x-1)=3
y=x-1
x+2y=3
当堂检测
3.下列是用代入法解方程组
①
②
的开始
步骤,其中最简单、正确的是( )
A.由①,得y=3x-2 ③,把③代入②,得3x=11-2(3x-2).
B.由①,得 ③,把③代入②,得 .
C.由②,得 ③,把③代入①,得 .
D.把②代入 ①,得11-2y-y=2,(把3x看作一个整体)
D
当堂检测
4.解下列方程组:
(1)
解: ① ,
②
把①代入②得,3y+y=8,
解得y=2,
把y=2代入x=3y得x=6.
故原方程组的解为 .
解: ① ,
②
把①代入②得,5s+2(3s-5)=12,
解得s=2,
把s=2代入t=3s-5得t=1.
故原方程组的解为 .
(2)
所以原方程组的解是
x=4
y=1
当堂检测
5.解方程组
3x+2y=14 ①
x-y=3 ②
解:由②变形得x=y+3③
将③代入① ,得3(y+3)+2y=14
3y+9+2y=14
将y=1代入②,得 x=4
5y=5,y=1
当堂检测
6.李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植多少亩?
解: 设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10 ①
2000x+1500y=18000 ②
将由①得 y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
课堂小结
解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
变:用含一个未知数的式子表示另一个未知数
代:用这个式子替代另一个方程中相应未知数
求:求出两个未知数的值
写:写出方程组的解
https://www.21cnjy.com/help/help_extract.php
5.2.1求解二元一次方程组(1)
第五章
二元一次方程组
2021-2022学年八年级数学上册同步(北师版)
学习目标
1.掌握代入消元法解二元一次方程组的步骤。
2.了解解二元一次方程组的基本思路。
3.初步体会化归思想在数学学习中的运用。
导入新课
2.什么是二元一次方程组?
1.什么是二元一次方程
3.什么是二元一次方程组的解?
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
二元一次方程组中各个方程的公共解,叫做二元一次方程组的解.
导入新课
篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
(1)如果设胜的场数是x
,则负的场数是10-x,
可得一元一次方程
;
(2)如果设胜的场数是x
,负的场数是y,
可得二元一次方程组
那么怎样解这个二元一次方程组呢?
讲授新课
用代入法解二元一次方程组
一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
讲授新课
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
讲授新课
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
要点归纳
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
讲授新课
将y=1代入② ,得 x=4.
经检验, x=4,y=1适合原方程组.
所以原方程组的解是
x=5,
y=2.
解:将②代入①,得 3(y+3)+2y=14
3y +9+2y =14
5y=5
y=1.
例1:解方程组
3x+2y=14 ①
x=y+3 ②
检验可以口算或在草稿纸上验算,以后可以不必写出.
讲授新课
将y=2代入③ ,得 x=5.
所以原方程组的解是
x=5,
y=2.
解:由②,得 x=13-4y ③
将③代入①,得 2(13 - 4y)+3y=16
26 –8y +3y =16
-5y=-10
y=2
例2:解方程组
2x+3y=16 ①
x+4y=13 ②
归纳总结
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的另一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.
当堂检测
1.二元一次方程组 的解是( )
D
A.
C.
B.
D.
当堂检测
D
2.已知方程组 用代入法消去y后的方程是( )
A.x+x-1=3
B.x+2x-1=3
C.x+x-2=3
D.x+2(x-1)=3
y=x-1
x+2y=3
当堂检测
3.下列是用代入法解方程组
①
②
的开始
步骤,其中最简单、正确的是( )
A.由①,得y=3x-2 ③,把③代入②,得3x=11-2(3x-2).
B.由①,得 ③,把③代入②,得 .
C.由②,得 ③,把③代入①,得 .
D.把②代入 ①,得11-2y-y=2,(把3x看作一个整体)
D
当堂检测
4.解下列方程组:
(1)
解: ① ,
②
把①代入②得,3y+y=8,
解得y=2,
把y=2代入x=3y得x=6.
故原方程组的解为 .
解: ① ,
②
把①代入②得,5s+2(3s-5)=12,
解得s=2,
把s=2代入t=3s-5得t=1.
故原方程组的解为 .
(2)
所以原方程组的解是
x=4
y=1
当堂检测
5.解方程组
3x+2y=14 ①
x-y=3 ②
解:由②变形得x=y+3③
将③代入① ,得3(y+3)+2y=14
3y+9+2y=14
将y=1代入②,得 x=4
5y=5,y=1
当堂检测
6.李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植多少亩?
解: 设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10 ①
2000x+1500y=18000 ②
将由①得 y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
课堂小结
解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
变:用含一个未知数的式子表示另一个未知数
代:用这个式子替代另一个方程中相应未知数
求:求出两个未知数的值
写:写出方程组的解
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
