2021-2022学年黑龙江省哈尔滨市南岗区九年级(上)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年黑龙江省哈尔滨市南岗区九年级(上)期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 09:39:46 | ||
图片预览



文档简介
2021-2022学年黑龙江省哈尔滨市南岗区九年级第一学期期末数学试卷(五四学制)
一、选择题(每小题3分,共计30分)
1.﹣的倒数是( )
A.2 B.﹣2 C. D.
2.下列计算正确的是( )
A.a a2=a2 B.(a2)3=a5
C.a+a2=a3 D.(ab2)2=a2b4
3.围成下列立体图形的各个面中,每个面都是平面的是( )
A.圆柱体 B.圆锥体 C.长方体 D.球体
4.抛物线y=(x+1)2﹣3的对称轴是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣3 D.直线x=3
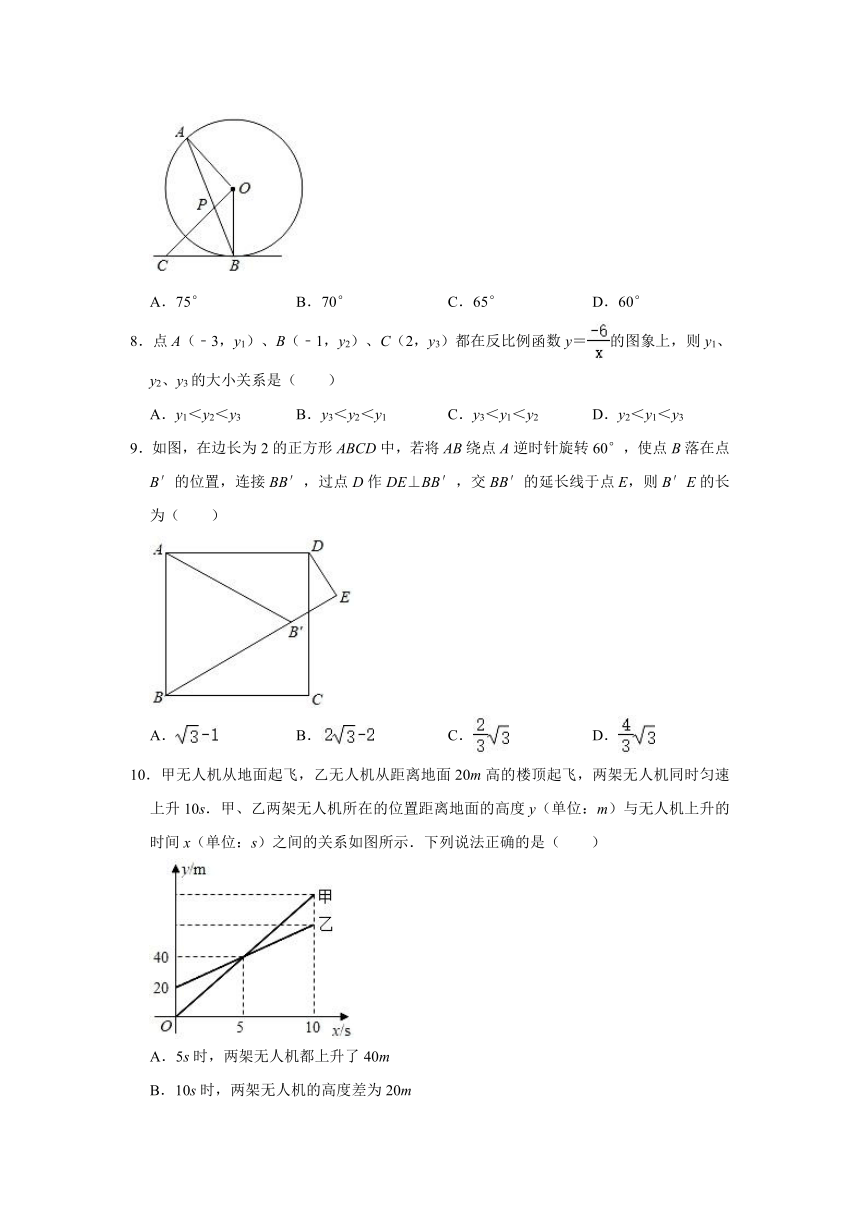
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
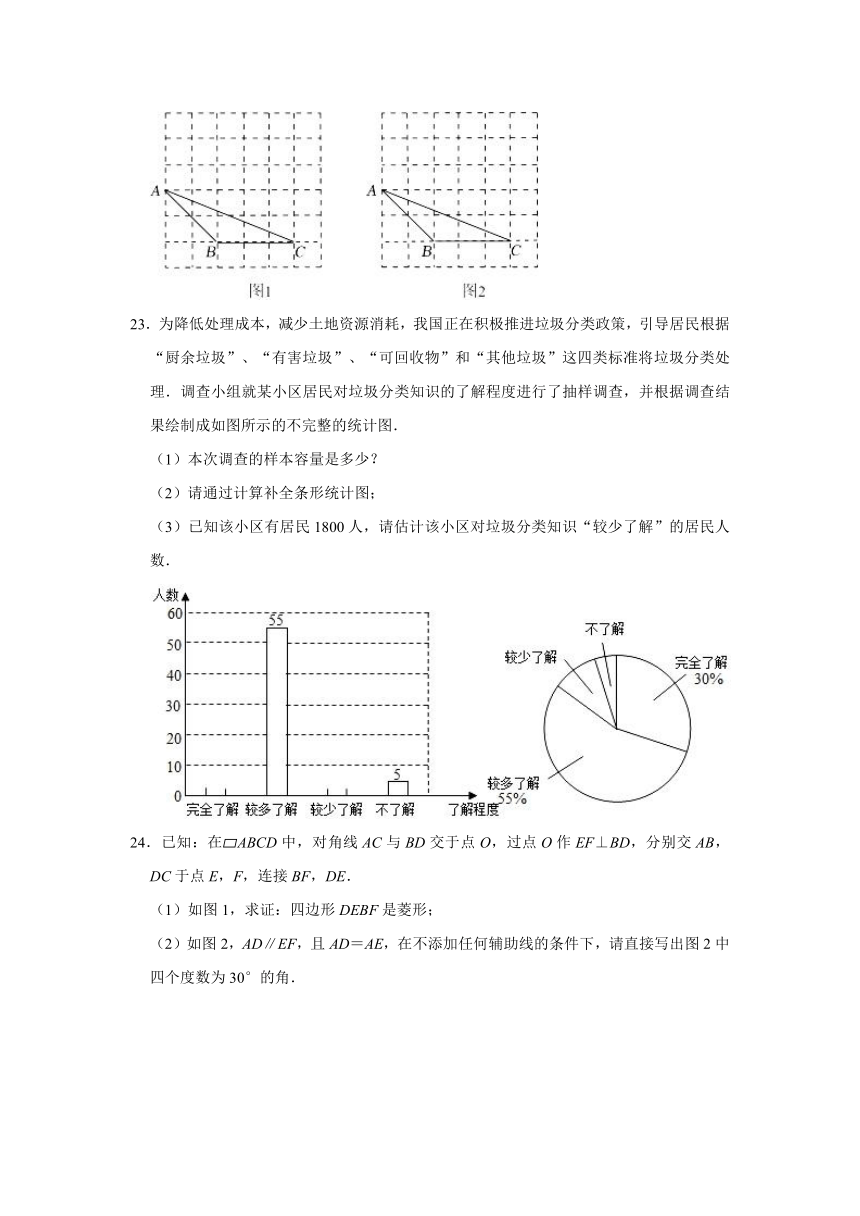
A. B.
C. D.
6.分式方程=的解是( )
A.x=2 B.x=4 C.x=6 D.x=8
7.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于( )
A.75° B.70° C.65° D.60°
8.点A(﹣3,y1)、B(﹣1,y2)、C(2,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
9.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长为( )
A. B. C. D.
10.甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )
A.5s时,两架无人机都上升了40m
B.10s时,两架无人机的高度差为20m
C.乙无人机上升的速度为8m/s
D.10s时,甲无人机距离地面的高度是60m
二、填空题(每小题3分,共计30分)
11.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资110200000元资金.数据110200000用科学记数法可表示为 .
12.函数y=中,自变量x的取值范围是 .
13.把多项式a3﹣2a2+a分解因式的结果是 .
14.计算+的结果是 .
15.已知反比例函数y=的图象经过点A(1,﹣2),则k= .
16.不等式组的解集是 .
17.在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同,摇匀后从中摸出一个球,记下颜色后再放回袋中,不断重复这一过程,共摸球100次,其中有40次摸到黑球,估计袋中红球的个数是 .
18.一个扇形的弧长是10πcm,面积是200πcm2,则这个扇形的圆心角是 度.
19.已知△ABC的三个顶点都是边长为6的同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,则点D到直线AB的距离为 .
20.如图,在△ABC中,AB=AC,点D在BC边上,BD=AC,CD=2,连接AD,若AD=2,则AC的长为 .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.先化简,再求代数式(1+)÷的值,其中a=5﹣20.
22.已知:在6×6的网格中,△ABC的三个顶点都在格点上.
(1)在图1中,画出△ACD,使△ACD与△ACB全等,顶点D在格点上且不与点B重合;
(2)在图2中,过点B画出平分△ABC面积的直线l.
23.为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾”、“有害垃圾”、“可回收物”和“其他垃圾”这四类标准将垃圾分类处理.调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制成如图所示的不完整的统计图.
(1)本次调查的样本容量是多少?
(2)请通过计算补全条形统计图;
(3)已知该小区有居民1800人,请估计该小区对垃圾分类知识“较少了解”的居民人数.
24.已知:在 ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.
(1)如图1,求证:四边形DEBF是菱形;
(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.
25.为进一步落实“德、智、体、美、劳”五育并举工作,某中学以体育为突破口,准备从体育用品商场一次性购买若干个足球和篮球,用于学校球类比赛活动.每个足球的价格都相同,每个篮球的价格也相同.已知篮球的单价比足球单价的2倍少30元,用1200元购买足球的数量是用900元购买篮球数量的2倍.
(1)足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共200个,但要求足球和篮球的总费用不超过15000元,学校需要最少购买多少个足球?
26.已知:△ABC内接于⊙O,连接AO并延长交BC于点D,且AD⊥BC于点D.
(1)如图1,求证:∠B=∠C;
(2)如图2,点E在上,连接AE,CE,∠ACE=∠ACB,求证:∠CAE=2∠ACE;
(3)如图3,在(2)的条件下,过点A作AF⊥CE交CE的延长线于点F,若AE=5,AB=13,求AF的长.
27.如图,经过点C(﹣2,﹣3)的抛物线y=ax2+x﹣交x轴于A、B两点.
(1)求抛物线的解析式;
(2)连接AC,点D在线段OA上,过点D作x轴的垂线交AC的延长线于点E,连接CD,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点F为BD的中点,连接BC,BE,CF,若∠AFC=2∠CBE,求S的值.
参考答案
一、选择题(每小题3分,共计30分)
1.﹣的倒数是( )
A.2 B.﹣2 C. D.
【分析】利用倒数的定义:乘积是1的两数互为倒数,进而得出答案.
解:∵﹣2×(﹣)=1,
∴﹣的倒数是﹣2.
故选:B.
2.下列计算正确的是( )
A.a a2=a2 B.(a2)3=a5
C.a+a2=a3 D.(ab2)2=a2b4
【分析】利用同底数幂的乘法的法则,幂的乘方与积的乘方的法则,合并同类项的法则对各项进行运算即可.
解:A、a a2=a3,故A不符合题意;
B、(a2)3=a6,故B不符合题意;
C、a与a2不属于同类项,不能合并,故C不符合题意;
D、(ab2)2=a2b4,故D符合题意;
故选:D.
3.围成下列立体图形的各个面中,每个面都是平面的是( )
A.圆柱体 B.圆锥体 C.长方体 D.球体
【分析】根据图形观察,围成立体图形的各个面是平面还是曲面逐一判断即可.
解:A.圆柱体是由平面和曲面围成,故A不符合题意;
B.圆锥体是由平面和曲面围成,故B不符合题意;
C.长方体是由平面围成的,故C符合题意;
D.球体是由曲面围成的,故D不符合题意;
故选:C.
4.抛物线y=(x+1)2﹣3的对称轴是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣3 D.直线x=3
【分析】根据抛物线的顶点式,可以写出该抛物线的对称轴,本题得以解决.
解:∵抛物线y=(x+1)2﹣3,
∴该抛物线的对称轴是直线x=﹣1,
故选:A.
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.是轴对称图形,不是中心对称图形,故本选项不合题意;
B.既是轴对称图形,又是中心对称图形,故本选项符合题意;
C.不是轴对称图形,是中心对称图形,故本选项不合题意;
D.不是轴对称图形,是中心对称图形,故本选项不合题意.
故选:B.
6.分式方程=的解是( )
A.x=2 B.x=4 C.x=6 D.x=8
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:20=2(x+4),
解得:x=6,
检验:把x=6代入得:5(x+4)≠0,
∴分式方程的解为x=6.
故选:C.
7.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于( )
A.75° B.70° C.65° D.60°
【分析】先利用对顶角相等和互余得到∠A=20°,再利用等腰三角形的性质得到∠OBA=∠A=20°,然后根据切线的性质得到OB⊥BC,从而利用互余计算出∠ABC的度数.
解:∵OC⊥OA,
∴∠AOC=90°,
∵∠APO=∠BPC=70°,
∴∠A=90°﹣70°=20°,
∵OA=OB,
∴∠OBA=∠A=20°,
∵BC为⊙O的切线,
∴OB⊥BC,
∴∠OBC=90°,
∴∠ABC=90°﹣20°=70°.
故选:B.
8.点A(﹣3,y1)、B(﹣1,y2)、C(2,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
【分析】分别把A、B、C各点坐标代入反比例函数y=求出y1、y2、y3的值,再比较大小即可.
解:∵点A(﹣3,y1),B(﹣1,y2),C(2,y3)都在反比例函数y=的图象上,
∴y1==2,y2==6,y3==﹣3,
∵﹣3<2<6,
∴y3<y1<y2,
故选:C.
9.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长为( )
A. B. C. D.
【分析】分别延长AD和BE交于点F,利用特殊角三角函数求出EF的长,根据△ABB'是等边三角形,求出B'E=BF﹣BB'﹣EF即可.
解:分别延长AD和BE交于点F,
由题知,AB=2,∠ABF=60°,
∴BF=AB÷cos60°=2÷=4,AF=BF sin60°=4×=2,∠F=90°﹣∠ABF=30°,
∴DF=AF﹣AD=2﹣2,
∴EF=DF cos∠F=(2)×=3﹣,
由题知,△ABB'是等边三角形,
∴B'E=BF﹣BB'﹣EF=4﹣2﹣(3﹣)=﹣1,
故选:A.
10.甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )
A.5s时,两架无人机都上升了40m
B.10s时,两架无人机的高度差为20m
C.乙无人机上升的速度为8m/s
D.10s时,甲无人机距离地面的高度是60m
【分析】根据题意和函数图象中的数据,可以计算出甲、乙两架无人机的速度,然后即可判断各个选项中的说法是否正确,本题得以解决.
解:由图象可得,
5s时,甲无人机上升了40m,乙无人机上升了40﹣20=20(m),故选项A错误;
甲无人机的速度为:40÷5=8(m/s),乙无人机的速度为:(40﹣20)÷5=4(m/s),故选项C错误;
则10s时,两架无人机的高度差为:(8×10)﹣(20+4×10)=20(m),故选项B正确;
10s时,甲无人机距离地面的高度是8×10=80(m),故选项D错误;
故选:B.
二、填空题(每小题3分,共计30分)
11.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资110200000元资金.数据110200000用科学记数法可表示为 1.102×108 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:数据110200000用科学记数法可表示为1.102×108.
故答案为:1.102×108.
12.函数y=中,自变量x的取值范围是 x≠ .
【分析】根据分母不为零是分式有意义的条件,可得答案.
解:由题意,得
2x﹣1≠0,解得x≠,
故答案为:x≠.
13.把多项式a3﹣2a2+a分解因式的结果是 a(a﹣1)2 .
【分析】先提取公因式a,再利用完全平方公式进行二次分解因式
解:a3﹣2a2+a
=a(a2﹣2a+1)
=a(a﹣1)2.
故答案为:a(a﹣1)2.
14.计算+的结果是 5 .
【分析】利用二次根式的加减法法则运算即可.
解:原式=2=5,
故答案为:5.
15.已知反比例函数y=的图象经过点A(1,﹣2),则k= ﹣2 .
【分析】直接把点A(1,﹣2)代入y=求出k的值即可.
解:∵反比例函数y=的图象经过点A(1,﹣2),
∴﹣2=,
解得k=﹣2.
故答案为:﹣2.
16.不等式组的解集是 1≤x<3 .
【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解:,
由①得:x<3,
由②得:x≥1,
∴不等式组的解集为1≤x<3.
故答案为:1≤x<3.
17.在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同,摇匀后从中摸出一个球,记下颜色后再放回袋中,不断重复这一过程,共摸球100次,其中有40次摸到黑球,估计袋中红球的个数是 6 .
【分析】利用频率估计概率可估计摸到黑球的概率为,然后根据概率公式构建方程求解即可.
解:设袋中红球的个数是x个,根据题意得:
=,
解得:x=6,
经检验:x=6是分式方程的解,
即估计袋中红球的个数是6个,
故答案为6.
18.一个扇形的弧长是10πcm,面积是200πcm2,则这个扇形的圆心角是 45 度.
【分析】利用扇形面积公式求出R的值,再利用扇形面积公式计算即可得到圆心角度数.
解:∵一个扇形的弧长是10πcm,面积是200πcm2,
∴S=Rl,即200π=×R×10π,
解得:R=40,
∴S=200π=,
解得:n=45°,
故答案为:45.
19.已知△ABC的三个顶点都是边长为6的同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,则点D到直线AB的距离为 3或6﹣6 .
【分析】分两种情况:①当B为直角顶点时,过D作DH⊥AB于H,由△AHD和△BHD是等腰直角三角形可得AH=DH=BH=3,则点D到直线AB的距离为3;②当B不是直角顶点时,过D作DH⊥BC于H,由△CDH是等腰直角三角形,得AD=DH=CH,证明△ABD≌△HBD(AAS),有AB=BH,即可求解.
解:①当B为直角顶点时,过D作DH⊥AB于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△ABC是等腰直角三角形,∠ABD=∠ADH=45°,AD=CD=AC,
∴△AHD和△BHD是等腰直角三角形,
∴AH=DH=BH,
∴DH=BC=3,
∴点D到直线AB的距离为3;
②当B不是直角顶点时,过D作DH⊥BC于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△CDH是等腰直角三角形,AD=DH=CH,
在△ABD和△HBD中,
,
∴△ABD≌△HBD(AAS),
∴AB=BH=6,
∵AB=AC=6,
∴BC===6,
∴CH=BC﹣BH=6﹣6,
∴AD=6﹣6,即此时点D到直线AB的距离为6﹣6,
综上所述,点D到直线AB的距离为3或6﹣6,
故答案为:3或6﹣6.
20.如图,在△ABC中,AB=AC,点D在BC边上,BD=AC,CD=2,连接AD,若AD=2,则AC的长为 4 .
【分析】根据等腰三角形的“三线合一”性质,想到过点A作AE⊥BC,垂足为E,设AB=AC=BD=x,然后在Rt△AED和Rt△AEC中,分别利用勾股定理表示出AE2,建立等量关系即可解答.
解:过点A作AE⊥BC,垂足为E,
∵AB=AC,BD=AC,
∴设AB=AC=BD=x,
∵CD=2,
∴BC=BD+CD=x+2,
∵AB=AC,AE⊥BC,
∴BE=EC=1+x,
∴DE=BD﹣BE=x﹣1,
在Rt△AED中,AE2=AD2﹣DE2=()2﹣(x﹣1)2=+x+7,
在Rt△AEC中,AE2=AC2﹣EC2=x2﹣(1+x)2=﹣x﹣1,
∴+x+7=﹣x﹣1,
解得:x1=4,x2=﹣2(不符合题意,舍去),
∴AC=4,
故答案为:4.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.先化简,再求代数式(1+)÷的值,其中a=5﹣20.
【分析】根据分式的减法以及乘除运算进行化简,然后将a的值代入化简后的式子即可求出答案.
解:原式=÷
=
=,
当a=5﹣20=﹣1时,
原式==.
22.已知:在6×6的网格中,△ABC的三个顶点都在格点上.
(1)在图1中,画出△ACD,使△ACD与△ACB全等,顶点D在格点上且不与点B重合;
(2)在图2中,过点B画出平分△ABC面积的直线l.
【分析】(1)构造平行四边形ABCD即可;
(2)过AC的中点D和点B作直线l即可.
解:(1)如图,△ADC即为所求;
(2)如图,直线l即为所求.
23.为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾”、“有害垃圾”、“可回收物”和“其他垃圾”这四类标准将垃圾分类处理.调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制成如图所示的不完整的统计图.
(1)本次调查的样本容量是多少?
(2)请通过计算补全条形统计图;
(3)已知该小区有居民1800人,请估计该小区对垃圾分类知识“较少了解”的居民人数.
【分析】(1)根据较多了解的人数是55人,占总人数的55%,即可求得本次调查的样本容量;
(2)求出完全了解、较少了解的人数,据此补全条形统计图;
(3)用总人数乘以“较少了解”人数所占的百分比即可.
解:(1)本次调查的样本容量是:55÷55%=100;
(2)完全了解的人数为:100×30%=30(人),
较少了解的人数为:100﹣30﹣55﹣5=10(人),
补全条形统计图如下:
(3)估计该小区对垃圾分类知识“较少了解”的居民人数为:1800×=180(人).
24.已知:在 ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.
(1)如图1,求证:四边形DEBF是菱形;
(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.
【分析】(1)证△DOF≌△BOE(ASA),得到DF∥BE,DF=BE,则四边形DEBF为平行四边形,再根据对角线互相垂直的平行四边形是菱形从而证得结论;
(2)证四边形ADFE是平行四边形,得AE=DF,再证△ADE是等边三角形,得∠AED=60°,然后由等腰三角形的性质和三角形的外角性质得∠EDB=∠EBD=∠AED=30°,同理∠FDB=∠FBD=30°.
【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AD∥EF,
∴四边形ADFE是平行四边形,
∴AE=DF,
由(1)得:四边形DEBF是菱形,
∴DE=DF=BE,
∴AD=DE,
∵AD=AE,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
∵DE=BE,
∴∠EDB=∠EBD=∠AED=30°,
同理:∠FDB=∠FBD=30°,
即图2中四个度数为30°的角为∠EDB、∠EBD、∠FDB、∠FBD.
25.为进一步落实“德、智、体、美、劳”五育并举工作,某中学以体育为突破口,准备从体育用品商场一次性购买若干个足球和篮球,用于学校球类比赛活动.每个足球的价格都相同,每个篮球的价格也相同.已知篮球的单价比足球单价的2倍少30元,用1200元购买足球的数量是用900元购买篮球数量的2倍.
(1)足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共200个,但要求足球和篮球的总费用不超过15000元,学校需要最少购买多少个足球?
【分析】(1)设足球的单价是x元,则篮球的单价是(2x﹣30)元,根据数量=总价÷单价,结合用1200元购买足球的数量是用900元购买篮球数量的2倍,列出分式方程,解方程即可;
(2)设学校可以购买m足球,则可以购买(200﹣m)个篮球,利用总价=单价×数量,结合购买足球和篮球的总费用不超过15000元,列出一元一次不等式,解不等式即可.
解:(1)设足球的单价是x元,则篮球的单价是(2x﹣30)元,
依题意得:=2×,
解得:x=60,
经检验,x=60是原方程的解,且符合题意,
∴2x﹣30=90.
答:足球的单价是60元,篮球的单价是90元.
(2)设学校可以购买m个足球,则可以购买(200﹣m)个篮球,
依题意得:60m+90(200﹣m)≤15000,
解得:m≥100,
答:学校最少可以购买100个足球.
26.已知:△ABC内接于⊙O,连接AO并延长交BC于点D,且AD⊥BC于点D.
(1)如图1,求证:∠B=∠C;
(2)如图2,点E在上,连接AE,CE,∠ACE=∠ACB,求证:∠CAE=2∠ACE;
(3)如图3,在(2)的条件下,过点A作AF⊥CE交CE的延长线于点F,若AE=5,AB=13,求AF的长.
【分析】(1)由垂径定理可得BD=CD,由垂直平分线的性质可得AB=AC;
(2)连接BE,设∠ACE=α,则∠ACB=3α,由圆周角定理得出∠ABE=∠ACE=α,可证出∠CAE=∠CBE=2α=2∠ACE;
(3)过点E作EG⊥AC于点G,在CG上截取GH=AG,连接EH,证出CH=EH=5,由勾股定理求出EG和CE的长,根据三角形ACE的面积可求出答案.
【解答】(1)证明:∵AD⊥BC,AD过圆心O,
∴BD=CD,且AD⊥BC,
∴AB=AC,
∴∠B=∠C;
(2)证明:连接BE,
设∠ACE=α,则∠ACB=3α,
∴∠ABC=∠ACB=3α,
∵∠ABE=∠ACE=α,
∴∠CBE=∠ABC﹣∠ABE=3α﹣α=2α,
∴∠CAE=∠CBE=2α=2∠ACE;
(3)解:过点E作EG⊥AC于点G,在CG上截取GH=AG,连接EH,
∴EH=AE=5,
∴∠AHE=∠EAH=2α,
∴∠CEH=∠AHE﹣∠ECH=2α﹣α=α=∠ECH,
∴CH=EH=5,
∵AC=AB=13,
∴AH=AC﹣CH=13﹣5=8,
∴AG=GH=4,
∴CG=4+5=9,
在Rt△AEG中,EG===3,
在Rt△CEG中,CE===3,
∵,
∴,
∴.
27.如图,经过点C(﹣2,﹣3)的抛物线y=ax2+x﹣交x轴于A、B两点.
(1)求抛物线的解析式;
(2)连接AC,点D在线段OA上,过点D作x轴的垂线交AC的延长线于点E,连接CD,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点F为BD的中点,连接BC,BE,CF,若∠AFC=2∠CBE,求S的值.
【分析】(1)运用待定系数法即可求得答案;
(2)如图1,令y=0,可求得A(﹣5,0),B(1,0),再运用待定系数法求得直线AC的解析式为y=﹣x﹣5,设D(t,0),则E(t,﹣t﹣5),可得DE=t+5,即可求得答案;
(3)如图2,在线段AC上截取CH=CE,连接BH,过点H作HK⊥BE于点K,过点C作CG⊥AB于点G,则∠CGF=∠AGC=∠BKH=90°,根据F是BD的中点,可得F(,0),由△BCE≌△BCH(SAS),可得BH=BE=,∠CBE=∠CBH,进而得出∠EBH=2∠CBE,利用面积法求出HK,再运用三角函数定义求得sin∠EBH==,sin∠AFC==,由∠AFC=2∠CBE,可得∠AFC=∠EBH,推出sin∠AFC=sin∠EBH,建立方程求解即可.
解:(1)∵抛物线y=ax2+x﹣经过C(﹣2,﹣3),
∴﹣3=a×(﹣2)2+×(﹣2)﹣,
解得:a=,
∴抛物线的解析式为y=x2+x﹣;
(2)如图1,在y=x2+x﹣中,令y=0,
则x2+x﹣=0,
解得:x1=﹣5,x2=1,
∴A(﹣5,0),B(1,0),
设直线AC的解析式为y=kx+b,
∵A(﹣5,0),C(﹣2,﹣3),
∴,
解得:,
∴直线AC的解析式为y=﹣x﹣5,
设D(t,0),则E(t,﹣t﹣5),
∴DE=t+5,
∴S= DE (xD﹣xC)=×(t+5)×(t+2)=t2+t+5,
∴S与t的函数解析式为S=t2+t+5;
(3)如图2,在线段AC上截取CH=CE,连接BH,过点H作HK⊥BE于点K,过点C作CG⊥AB于点G,
则∠CGF=∠AGC=∠BKH=90°,
由(2)知:A(﹣5,0),B(1,0),C(﹣2,﹣3),D(t,0),E(t,﹣t﹣5),
∵F是BD的中点,
∴F(,0),
∵G(﹣2,0),
∴AG=BG=CG=3,
∴∠CAG=∠ACG=∠BCG=∠CBG=45°,BC=3,
∴∠ACB=∠BCE=90°,
∵DG=t+2,
∴CE=CH=(t+2),
∴EH=2(t+2),
在Rt△BED中,BE===,
在△BCE和△BCH中,
,
∴△BCE≌△BCH(SAS),
∴BH=BE=,∠CBE=∠CBH,
∴∠EBH=2∠CBE,
∵S△BEH=EH BC=BE HK,
∴HK==,
∴sin∠EBH==,
在Rt△CFG中,CF===,
∴sin∠AFC==,
∵∠AFC=2∠CBE,
∴∠AFC=∠EBH,
∴sin∠AFC=sin∠EBH,
∴=,
整理得:(2t+1)(t+5)2=0,
∴t=﹣或t=﹣5(舍去),
当t=﹣时,
S=t2+t+5=×(﹣)2+×(﹣)+5=,
故S的值为.
一、选择题(每小题3分,共计30分)
1.﹣的倒数是( )
A.2 B.﹣2 C. D.
2.下列计算正确的是( )
A.a a2=a2 B.(a2)3=a5
C.a+a2=a3 D.(ab2)2=a2b4
3.围成下列立体图形的各个面中,每个面都是平面的是( )
A.圆柱体 B.圆锥体 C.长方体 D.球体
4.抛物线y=(x+1)2﹣3的对称轴是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣3 D.直线x=3
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
6.分式方程=的解是( )
A.x=2 B.x=4 C.x=6 D.x=8
7.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于( )
A.75° B.70° C.65° D.60°
8.点A(﹣3,y1)、B(﹣1,y2)、C(2,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
9.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长为( )
A. B. C. D.
10.甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )
A.5s时,两架无人机都上升了40m
B.10s时,两架无人机的高度差为20m
C.乙无人机上升的速度为8m/s
D.10s时,甲无人机距离地面的高度是60m
二、填空题(每小题3分,共计30分)
11.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资110200000元资金.数据110200000用科学记数法可表示为 .
12.函数y=中,自变量x的取值范围是 .
13.把多项式a3﹣2a2+a分解因式的结果是 .
14.计算+的结果是 .
15.已知反比例函数y=的图象经过点A(1,﹣2),则k= .
16.不等式组的解集是 .
17.在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同,摇匀后从中摸出一个球,记下颜色后再放回袋中,不断重复这一过程,共摸球100次,其中有40次摸到黑球,估计袋中红球的个数是 .
18.一个扇形的弧长是10πcm,面积是200πcm2,则这个扇形的圆心角是 度.
19.已知△ABC的三个顶点都是边长为6的同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,则点D到直线AB的距离为 .
20.如图,在△ABC中,AB=AC,点D在BC边上,BD=AC,CD=2,连接AD,若AD=2,则AC的长为 .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.先化简,再求代数式(1+)÷的值,其中a=5﹣20.
22.已知:在6×6的网格中,△ABC的三个顶点都在格点上.
(1)在图1中,画出△ACD,使△ACD与△ACB全等,顶点D在格点上且不与点B重合;
(2)在图2中,过点B画出平分△ABC面积的直线l.
23.为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾”、“有害垃圾”、“可回收物”和“其他垃圾”这四类标准将垃圾分类处理.调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制成如图所示的不完整的统计图.
(1)本次调查的样本容量是多少?
(2)请通过计算补全条形统计图;
(3)已知该小区有居民1800人,请估计该小区对垃圾分类知识“较少了解”的居民人数.
24.已知:在 ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.
(1)如图1,求证:四边形DEBF是菱形;
(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.
25.为进一步落实“德、智、体、美、劳”五育并举工作,某中学以体育为突破口,准备从体育用品商场一次性购买若干个足球和篮球,用于学校球类比赛活动.每个足球的价格都相同,每个篮球的价格也相同.已知篮球的单价比足球单价的2倍少30元,用1200元购买足球的数量是用900元购买篮球数量的2倍.
(1)足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共200个,但要求足球和篮球的总费用不超过15000元,学校需要最少购买多少个足球?
26.已知:△ABC内接于⊙O,连接AO并延长交BC于点D,且AD⊥BC于点D.
(1)如图1,求证:∠B=∠C;
(2)如图2,点E在上,连接AE,CE,∠ACE=∠ACB,求证:∠CAE=2∠ACE;
(3)如图3,在(2)的条件下,过点A作AF⊥CE交CE的延长线于点F,若AE=5,AB=13,求AF的长.
27.如图,经过点C(﹣2,﹣3)的抛物线y=ax2+x﹣交x轴于A、B两点.
(1)求抛物线的解析式;
(2)连接AC,点D在线段OA上,过点D作x轴的垂线交AC的延长线于点E,连接CD,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点F为BD的中点,连接BC,BE,CF,若∠AFC=2∠CBE,求S的值.
参考答案
一、选择题(每小题3分,共计30分)
1.﹣的倒数是( )
A.2 B.﹣2 C. D.
【分析】利用倒数的定义:乘积是1的两数互为倒数,进而得出答案.
解:∵﹣2×(﹣)=1,
∴﹣的倒数是﹣2.
故选:B.
2.下列计算正确的是( )
A.a a2=a2 B.(a2)3=a5
C.a+a2=a3 D.(ab2)2=a2b4
【分析】利用同底数幂的乘法的法则,幂的乘方与积的乘方的法则,合并同类项的法则对各项进行运算即可.
解:A、a a2=a3,故A不符合题意;
B、(a2)3=a6,故B不符合题意;
C、a与a2不属于同类项,不能合并,故C不符合题意;
D、(ab2)2=a2b4,故D符合题意;
故选:D.
3.围成下列立体图形的各个面中,每个面都是平面的是( )
A.圆柱体 B.圆锥体 C.长方体 D.球体
【分析】根据图形观察,围成立体图形的各个面是平面还是曲面逐一判断即可.
解:A.圆柱体是由平面和曲面围成,故A不符合题意;
B.圆锥体是由平面和曲面围成,故B不符合题意;
C.长方体是由平面围成的,故C符合题意;
D.球体是由曲面围成的,故D不符合题意;
故选:C.
4.抛物线y=(x+1)2﹣3的对称轴是( )
A.直线x=﹣1 B.直线x=1 C.直线x=﹣3 D.直线x=3
【分析】根据抛物线的顶点式,可以写出该抛物线的对称轴,本题得以解决.
解:∵抛物线y=(x+1)2﹣3,
∴该抛物线的对称轴是直线x=﹣1,
故选:A.
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:A.是轴对称图形,不是中心对称图形,故本选项不合题意;
B.既是轴对称图形,又是中心对称图形,故本选项符合题意;
C.不是轴对称图形,是中心对称图形,故本选项不合题意;
D.不是轴对称图形,是中心对称图形,故本选项不合题意.
故选:B.
6.分式方程=的解是( )
A.x=2 B.x=4 C.x=6 D.x=8
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:20=2(x+4),
解得:x=6,
检验:把x=6代入得:5(x+4)≠0,
∴分式方程的解为x=6.
故选:C.
7.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于( )
A.75° B.70° C.65° D.60°
【分析】先利用对顶角相等和互余得到∠A=20°,再利用等腰三角形的性质得到∠OBA=∠A=20°,然后根据切线的性质得到OB⊥BC,从而利用互余计算出∠ABC的度数.
解:∵OC⊥OA,
∴∠AOC=90°,
∵∠APO=∠BPC=70°,
∴∠A=90°﹣70°=20°,
∵OA=OB,
∴∠OBA=∠A=20°,
∵BC为⊙O的切线,
∴OB⊥BC,
∴∠OBC=90°,
∴∠ABC=90°﹣20°=70°.
故选:B.
8.点A(﹣3,y1)、B(﹣1,y2)、C(2,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
【分析】分别把A、B、C各点坐标代入反比例函数y=求出y1、y2、y3的值,再比较大小即可.
解:∵点A(﹣3,y1),B(﹣1,y2),C(2,y3)都在反比例函数y=的图象上,
∴y1==2,y2==6,y3==﹣3,
∵﹣3<2<6,
∴y3<y1<y2,
故选:C.
9.如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长为( )
A. B. C. D.
【分析】分别延长AD和BE交于点F,利用特殊角三角函数求出EF的长,根据△ABB'是等边三角形,求出B'E=BF﹣BB'﹣EF即可.
解:分别延长AD和BE交于点F,
由题知,AB=2,∠ABF=60°,
∴BF=AB÷cos60°=2÷=4,AF=BF sin60°=4×=2,∠F=90°﹣∠ABF=30°,
∴DF=AF﹣AD=2﹣2,
∴EF=DF cos∠F=(2)×=3﹣,
由题知,△ABB'是等边三角形,
∴B'E=BF﹣BB'﹣EF=4﹣2﹣(3﹣)=﹣1,
故选:A.
10.甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )
A.5s时,两架无人机都上升了40m
B.10s时,两架无人机的高度差为20m
C.乙无人机上升的速度为8m/s
D.10s时,甲无人机距离地面的高度是60m
【分析】根据题意和函数图象中的数据,可以计算出甲、乙两架无人机的速度,然后即可判断各个选项中的说法是否正确,本题得以解决.
解:由图象可得,
5s时,甲无人机上升了40m,乙无人机上升了40﹣20=20(m),故选项A错误;
甲无人机的速度为:40÷5=8(m/s),乙无人机的速度为:(40﹣20)÷5=4(m/s),故选项C错误;
则10s时,两架无人机的高度差为:(8×10)﹣(20+4×10)=20(m),故选项B正确;
10s时,甲无人机距离地面的高度是8×10=80(m),故选项D错误;
故选:B.
二、填空题(每小题3分,共计30分)
11.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资110200000元资金.数据110200000用科学记数法可表示为 1.102×108 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:数据110200000用科学记数法可表示为1.102×108.
故答案为:1.102×108.
12.函数y=中,自变量x的取值范围是 x≠ .
【分析】根据分母不为零是分式有意义的条件,可得答案.
解:由题意,得
2x﹣1≠0,解得x≠,
故答案为:x≠.
13.把多项式a3﹣2a2+a分解因式的结果是 a(a﹣1)2 .
【分析】先提取公因式a,再利用完全平方公式进行二次分解因式
解:a3﹣2a2+a
=a(a2﹣2a+1)
=a(a﹣1)2.
故答案为:a(a﹣1)2.
14.计算+的结果是 5 .
【分析】利用二次根式的加减法法则运算即可.
解:原式=2=5,
故答案为:5.
15.已知反比例函数y=的图象经过点A(1,﹣2),则k= ﹣2 .
【分析】直接把点A(1,﹣2)代入y=求出k的值即可.
解:∵反比例函数y=的图象经过点A(1,﹣2),
∴﹣2=,
解得k=﹣2.
故答案为:﹣2.
16.不等式组的解集是 1≤x<3 .
【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解:,
由①得:x<3,
由②得:x≥1,
∴不等式组的解集为1≤x<3.
故答案为:1≤x<3.
17.在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同,摇匀后从中摸出一个球,记下颜色后再放回袋中,不断重复这一过程,共摸球100次,其中有40次摸到黑球,估计袋中红球的个数是 6 .
【分析】利用频率估计概率可估计摸到黑球的概率为,然后根据概率公式构建方程求解即可.
解:设袋中红球的个数是x个,根据题意得:
=,
解得:x=6,
经检验:x=6是分式方程的解,
即估计袋中红球的个数是6个,
故答案为6.
18.一个扇形的弧长是10πcm,面积是200πcm2,则这个扇形的圆心角是 45 度.
【分析】利用扇形面积公式求出R的值,再利用扇形面积公式计算即可得到圆心角度数.
解:∵一个扇形的弧长是10πcm,面积是200πcm2,
∴S=Rl,即200π=×R×10π,
解得:R=40,
∴S=200π=,
解得:n=45°,
故答案为:45.
19.已知△ABC的三个顶点都是边长为6的同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,则点D到直线AB的距离为 3或6﹣6 .
【分析】分两种情况:①当B为直角顶点时,过D作DH⊥AB于H,由△AHD和△BHD是等腰直角三角形可得AH=DH=BH=3,则点D到直线AB的距离为3;②当B不是直角顶点时,过D作DH⊥BC于H,由△CDH是等腰直角三角形,得AD=DH=CH,证明△ABD≌△HBD(AAS),有AB=BH,即可求解.
解:①当B为直角顶点时,过D作DH⊥AB于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△ABC是等腰直角三角形,∠ABD=∠ADH=45°,AD=CD=AC,
∴△AHD和△BHD是等腰直角三角形,
∴AH=DH=BH,
∴DH=BC=3,
∴点D到直线AB的距离为3;
②当B不是直角顶点时,过D作DH⊥BC于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△CDH是等腰直角三角形,AD=DH=CH,
在△ABD和△HBD中,
,
∴△ABD≌△HBD(AAS),
∴AB=BH=6,
∵AB=AC=6,
∴BC===6,
∴CH=BC﹣BH=6﹣6,
∴AD=6﹣6,即此时点D到直线AB的距离为6﹣6,
综上所述,点D到直线AB的距离为3或6﹣6,
故答案为:3或6﹣6.
20.如图,在△ABC中,AB=AC,点D在BC边上,BD=AC,CD=2,连接AD,若AD=2,则AC的长为 4 .
【分析】根据等腰三角形的“三线合一”性质,想到过点A作AE⊥BC,垂足为E,设AB=AC=BD=x,然后在Rt△AED和Rt△AEC中,分别利用勾股定理表示出AE2,建立等量关系即可解答.
解:过点A作AE⊥BC,垂足为E,
∵AB=AC,BD=AC,
∴设AB=AC=BD=x,
∵CD=2,
∴BC=BD+CD=x+2,
∵AB=AC,AE⊥BC,
∴BE=EC=1+x,
∴DE=BD﹣BE=x﹣1,
在Rt△AED中,AE2=AD2﹣DE2=()2﹣(x﹣1)2=+x+7,
在Rt△AEC中,AE2=AC2﹣EC2=x2﹣(1+x)2=﹣x﹣1,
∴+x+7=﹣x﹣1,
解得:x1=4,x2=﹣2(不符合题意,舍去),
∴AC=4,
故答案为:4.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.先化简,再求代数式(1+)÷的值,其中a=5﹣20.
【分析】根据分式的减法以及乘除运算进行化简,然后将a的值代入化简后的式子即可求出答案.
解:原式=÷
=
=,
当a=5﹣20=﹣1时,
原式==.
22.已知:在6×6的网格中,△ABC的三个顶点都在格点上.
(1)在图1中,画出△ACD,使△ACD与△ACB全等,顶点D在格点上且不与点B重合;
(2)在图2中,过点B画出平分△ABC面积的直线l.
【分析】(1)构造平行四边形ABCD即可;
(2)过AC的中点D和点B作直线l即可.
解:(1)如图,△ADC即为所求;
(2)如图,直线l即为所求.
23.为降低处理成本,减少土地资源消耗,我国正在积极推进垃圾分类政策,引导居民根据“厨余垃圾”、“有害垃圾”、“可回收物”和“其他垃圾”这四类标准将垃圾分类处理.调查小组就某小区居民对垃圾分类知识的了解程度进行了抽样调查,并根据调查结果绘制成如图所示的不完整的统计图.
(1)本次调查的样本容量是多少?
(2)请通过计算补全条形统计图;
(3)已知该小区有居民1800人,请估计该小区对垃圾分类知识“较少了解”的居民人数.
【分析】(1)根据较多了解的人数是55人,占总人数的55%,即可求得本次调查的样本容量;
(2)求出完全了解、较少了解的人数,据此补全条形统计图;
(3)用总人数乘以“较少了解”人数所占的百分比即可.
解:(1)本次调查的样本容量是:55÷55%=100;
(2)完全了解的人数为:100×30%=30(人),
较少了解的人数为:100﹣30﹣55﹣5=10(人),
补全条形统计图如下:
(3)估计该小区对垃圾分类知识“较少了解”的居民人数为:1800×=180(人).
24.已知:在 ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.
(1)如图1,求证:四边形DEBF是菱形;
(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.
【分析】(1)证△DOF≌△BOE(ASA),得到DF∥BE,DF=BE,则四边形DEBF为平行四边形,再根据对角线互相垂直的平行四边形是菱形从而证得结论;
(2)证四边形ADFE是平行四边形,得AE=DF,再证△ADE是等边三角形,得∠AED=60°,然后由等腰三角形的性质和三角形的外角性质得∠EDB=∠EBD=∠AED=30°,同理∠FDB=∠FBD=30°.
【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AD∥EF,
∴四边形ADFE是平行四边形,
∴AE=DF,
由(1)得:四边形DEBF是菱形,
∴DE=DF=BE,
∴AD=DE,
∵AD=AE,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
∵DE=BE,
∴∠EDB=∠EBD=∠AED=30°,
同理:∠FDB=∠FBD=30°,
即图2中四个度数为30°的角为∠EDB、∠EBD、∠FDB、∠FBD.
25.为进一步落实“德、智、体、美、劳”五育并举工作,某中学以体育为突破口,准备从体育用品商场一次性购买若干个足球和篮球,用于学校球类比赛活动.每个足球的价格都相同,每个篮球的价格也相同.已知篮球的单价比足球单价的2倍少30元,用1200元购买足球的数量是用900元购买篮球数量的2倍.
(1)足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共200个,但要求足球和篮球的总费用不超过15000元,学校需要最少购买多少个足球?
【分析】(1)设足球的单价是x元,则篮球的单价是(2x﹣30)元,根据数量=总价÷单价,结合用1200元购买足球的数量是用900元购买篮球数量的2倍,列出分式方程,解方程即可;
(2)设学校可以购买m足球,则可以购买(200﹣m)个篮球,利用总价=单价×数量,结合购买足球和篮球的总费用不超过15000元,列出一元一次不等式,解不等式即可.
解:(1)设足球的单价是x元,则篮球的单价是(2x﹣30)元,
依题意得:=2×,
解得:x=60,
经检验,x=60是原方程的解,且符合题意,
∴2x﹣30=90.
答:足球的单价是60元,篮球的单价是90元.
(2)设学校可以购买m个足球,则可以购买(200﹣m)个篮球,
依题意得:60m+90(200﹣m)≤15000,
解得:m≥100,
答:学校最少可以购买100个足球.
26.已知:△ABC内接于⊙O,连接AO并延长交BC于点D,且AD⊥BC于点D.
(1)如图1,求证:∠B=∠C;
(2)如图2,点E在上,连接AE,CE,∠ACE=∠ACB,求证:∠CAE=2∠ACE;
(3)如图3,在(2)的条件下,过点A作AF⊥CE交CE的延长线于点F,若AE=5,AB=13,求AF的长.
【分析】(1)由垂径定理可得BD=CD,由垂直平分线的性质可得AB=AC;
(2)连接BE,设∠ACE=α,则∠ACB=3α,由圆周角定理得出∠ABE=∠ACE=α,可证出∠CAE=∠CBE=2α=2∠ACE;
(3)过点E作EG⊥AC于点G,在CG上截取GH=AG,连接EH,证出CH=EH=5,由勾股定理求出EG和CE的长,根据三角形ACE的面积可求出答案.
【解答】(1)证明:∵AD⊥BC,AD过圆心O,
∴BD=CD,且AD⊥BC,
∴AB=AC,
∴∠B=∠C;
(2)证明:连接BE,
设∠ACE=α,则∠ACB=3α,
∴∠ABC=∠ACB=3α,
∵∠ABE=∠ACE=α,
∴∠CBE=∠ABC﹣∠ABE=3α﹣α=2α,
∴∠CAE=∠CBE=2α=2∠ACE;
(3)解:过点E作EG⊥AC于点G,在CG上截取GH=AG,连接EH,
∴EH=AE=5,
∴∠AHE=∠EAH=2α,
∴∠CEH=∠AHE﹣∠ECH=2α﹣α=α=∠ECH,
∴CH=EH=5,
∵AC=AB=13,
∴AH=AC﹣CH=13﹣5=8,
∴AG=GH=4,
∴CG=4+5=9,
在Rt△AEG中,EG===3,
在Rt△CEG中,CE===3,
∵,
∴,
∴.
27.如图,经过点C(﹣2,﹣3)的抛物线y=ax2+x﹣交x轴于A、B两点.
(1)求抛物线的解析式;
(2)连接AC,点D在线段OA上,过点D作x轴的垂线交AC的延长线于点E,连接CD,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点F为BD的中点,连接BC,BE,CF,若∠AFC=2∠CBE,求S的值.
【分析】(1)运用待定系数法即可求得答案;
(2)如图1,令y=0,可求得A(﹣5,0),B(1,0),再运用待定系数法求得直线AC的解析式为y=﹣x﹣5,设D(t,0),则E(t,﹣t﹣5),可得DE=t+5,即可求得答案;
(3)如图2,在线段AC上截取CH=CE,连接BH,过点H作HK⊥BE于点K,过点C作CG⊥AB于点G,则∠CGF=∠AGC=∠BKH=90°,根据F是BD的中点,可得F(,0),由△BCE≌△BCH(SAS),可得BH=BE=,∠CBE=∠CBH,进而得出∠EBH=2∠CBE,利用面积法求出HK,再运用三角函数定义求得sin∠EBH==,sin∠AFC==,由∠AFC=2∠CBE,可得∠AFC=∠EBH,推出sin∠AFC=sin∠EBH,建立方程求解即可.
解:(1)∵抛物线y=ax2+x﹣经过C(﹣2,﹣3),
∴﹣3=a×(﹣2)2+×(﹣2)﹣,
解得:a=,
∴抛物线的解析式为y=x2+x﹣;
(2)如图1,在y=x2+x﹣中,令y=0,
则x2+x﹣=0,
解得:x1=﹣5,x2=1,
∴A(﹣5,0),B(1,0),
设直线AC的解析式为y=kx+b,
∵A(﹣5,0),C(﹣2,﹣3),
∴,
解得:,
∴直线AC的解析式为y=﹣x﹣5,
设D(t,0),则E(t,﹣t﹣5),
∴DE=t+5,
∴S= DE (xD﹣xC)=×(t+5)×(t+2)=t2+t+5,
∴S与t的函数解析式为S=t2+t+5;
(3)如图2,在线段AC上截取CH=CE,连接BH,过点H作HK⊥BE于点K,过点C作CG⊥AB于点G,
则∠CGF=∠AGC=∠BKH=90°,
由(2)知:A(﹣5,0),B(1,0),C(﹣2,﹣3),D(t,0),E(t,﹣t﹣5),
∵F是BD的中点,
∴F(,0),
∵G(﹣2,0),
∴AG=BG=CG=3,
∴∠CAG=∠ACG=∠BCG=∠CBG=45°,BC=3,
∴∠ACB=∠BCE=90°,
∵DG=t+2,
∴CE=CH=(t+2),
∴EH=2(t+2),
在Rt△BED中,BE===,
在△BCE和△BCH中,
,
∴△BCE≌△BCH(SAS),
∴BH=BE=,∠CBE=∠CBH,
∴∠EBH=2∠CBE,
∵S△BEH=EH BC=BE HK,
∴HK==,
∴sin∠EBH==,
在Rt△CFG中,CF===,
∴sin∠AFC==,
∵∠AFC=2∠CBE,
∴∠AFC=∠EBH,
∴sin∠AFC=sin∠EBH,
∴=,
整理得:(2t+1)(t+5)2=0,
∴t=﹣或t=﹣5(舍去),
当t=﹣时,
S=t2+t+5=×(﹣)2+×(﹣)+5=,
故S的值为.
同课章节目录
