2020-2021学年上海市浦东新区部分学校八年级(上)期末数学试卷(Word版含解析)
文档属性
| 名称 | 2020-2021学年上海市浦东新区部分学校八年级(上)期末数学试卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 810.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 09:54:28 | ||
图片预览



文档简介
2020-2021学年上海市浦东新区部分学校八年级第一学期期末数学试卷
一、选择题(共6题,每题2分,满分12分)
1.下列二次根式中,与属同类二次根式的是( )
A. B. C. D.
2.下列各数中,是方程2x2+5x=3的根的是( )
A.﹣3 B.﹣1 C.1 D.3
3.直线y=﹣x不经过点( )
A.(0,0) B.(﹣2,3) C.(3,﹣2) D.(﹣3,2)
4.用下列几组边长构成的三角形中哪一组不是直角三角形( )
A.8,15,17 B.,, C.,2, D.1,2,
5.下列命题中,逆命题是假命题的是( )
A.两直线平行,同旁内角互补
B.直角三角形的两个锐角互余
C.全等三角形的对应角相等
D.直角三角形两条直角边的平方和等于斜边的平方
6.已知在△ABC中,AB=2,AC=2,BC边上的高等于,那么BC的长是 ( )
A.2 B.4 C.2或4 D.无法确定.
二、填空题:(本大题共12题,每题3分,满分36分)
7.的有理化因式是 .
8.函数的定义域是 .
9.在实数范围内分解因式:2x2﹣3x﹣1= .
10.已知关于x的一元二次方程mx2﹣2x+1=0有两个不相等的实数根,那么m的取值范围是 .
11.已知函数f(x)=,那么f(2)= .
12.我们学校响应国家对垃圾分类处理的号召,组织同学们积极学习垃圾分类相关知识.初二年级某班每月进行一次垃圾分类知识测试,结果显示9月份32名同学测试结果优秀,到11月份增加到38名同学测试结果优秀,设平均每月优秀人数增长的百分率为x,则可以列出的方程是 .
13.已知P(x1,y1),Q(x2,y2)在反比例函数的图象上,若x1<x2<0,则y1 y2
(填“>”“<”或“=”).
14.如果点A的坐标为(2,﹣1),点B的坐标为(5,3),那么A、B两点的距离等于 .
15.到点P的距离等于5的点的轨迹是 .
16.在△ABC中,AB=10,BC=8,∠B=60°,则AC的长度是 .
17.如图,点P是∠AOB的角平分线上的一点,过点P作PC∥OA交OB于点C,PD⊥OA,若∠AOB=60°,OC=2,则PD= .
18.如图,将长方形ABCD绕点A顺时针旋转,点D落在边BC上的点D′处,点B、C分别落在点B′、点C′处,如果∠D′BC′=∠D′C′B,那么DC:D′C的比值等于 .
三、简答题:(本大题共4题,每题6分,满分24分)
19.计算:.
20.解方程:(x2﹣9)+x(x﹣3)=0.
21.已知y=y1+y2,y1与x﹣1成正比例,y2与x成反比例,且当x=2时,y=1;当x=﹣2时,y=﹣2,求y关于x的函数解析式.
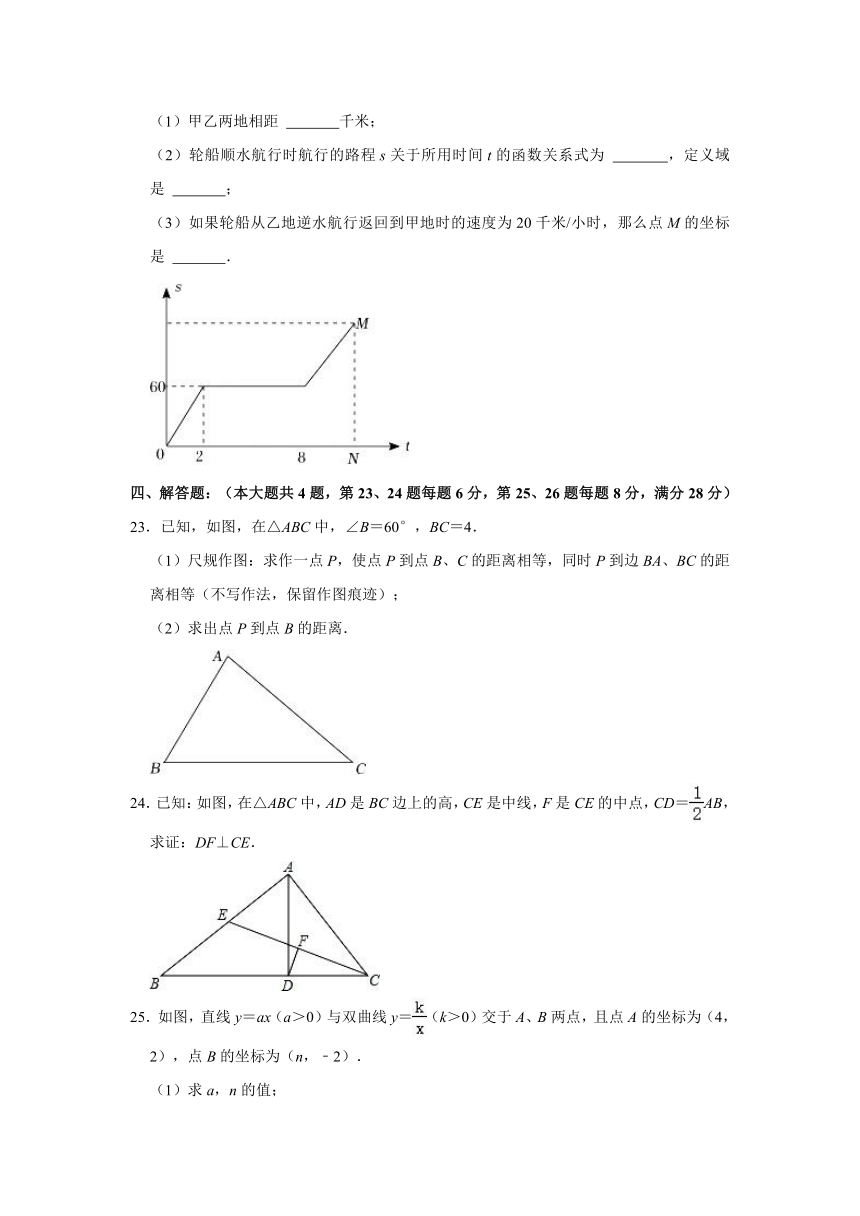
22.一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用的时间为t(小时),航行的路程为s(千米),s与t的函数图象如图所示.
(1)甲乙两地相距 千米;
(2)轮船顺水航行时航行的路程s关于所用时间t的函数关系式为 ,定义域是 ;
(3)如果轮船从乙地逆水航行返回到甲地时的速度为20千米/小时,那么点M的坐标是 .
四、解答题:(本大题共4题,第23、24题每题6分,第25、26题每题8分,满分28分)
23.已知,如图,在△ABC中,∠B=60°,BC=4.
(1)尺规作图:求作一点P,使点P到点B、C的距离相等,同时P到边BA、BC的距离相等(不写作法,保留作图痕迹);
(2)求出点P到点B的距离.
24.已知:如图,在△ABC中,AD是BC边上的高,CE是中线,F是CE的中点,CD=AB,求证:DF⊥CE.
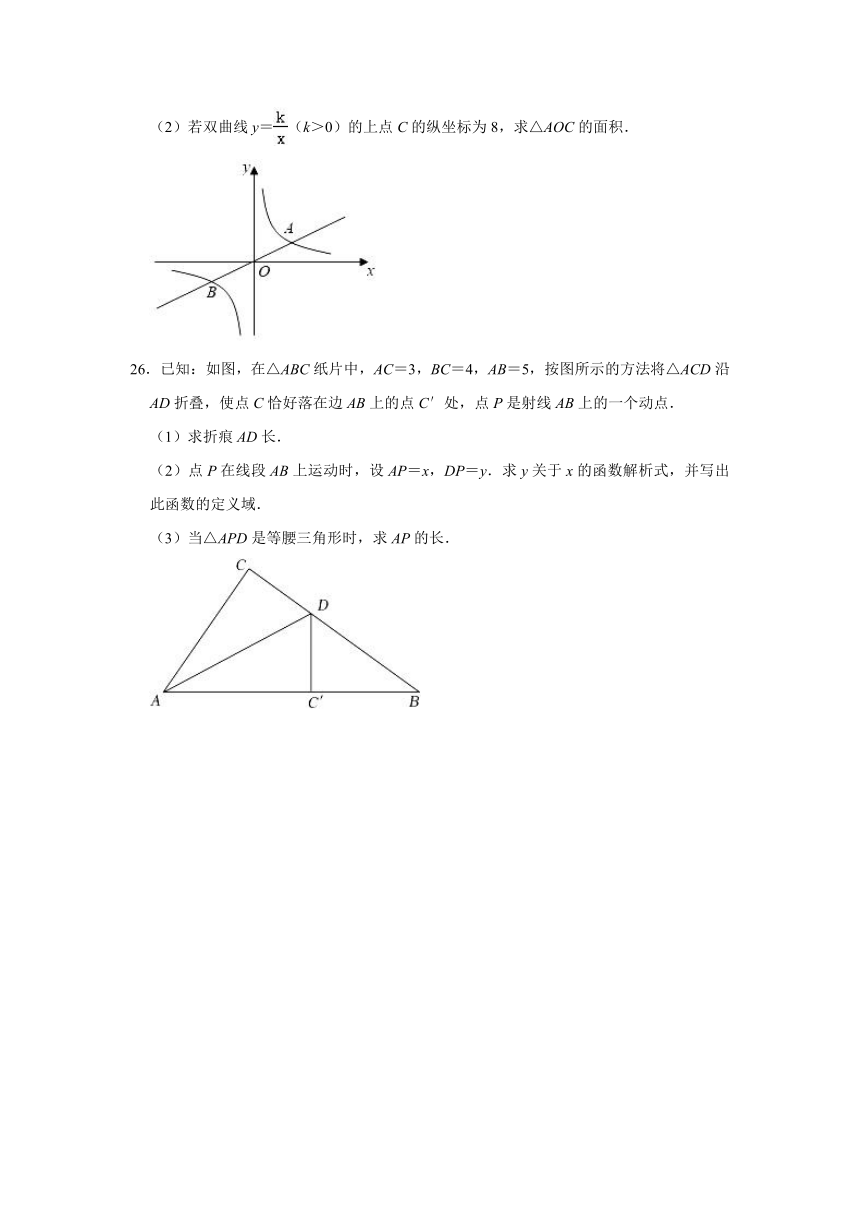
25.如图,直线y=ax(a>0)与双曲线y=(k>0)交于A、B两点,且点A的坐标为(4,2),点B的坐标为(n,﹣2).
(1)求a,n的值;
(2)若双曲线y=(k>0)的上点C的纵坐标为8,求△AOC的面积.
26.已知:如图,在△ABC纸片中,AC=3,BC=4,AB=5,按图所示的方法将△ACD沿AD折叠,使点C恰好落在边AB上的点C′处,点P是射线AB上的一个动点.
(1)求折痕AD长.
(2)点P在线段AB上运动时,设AP=x,DP=y.求y关于x的函数解析式,并写出此函数的定义域.
(3)当△APD是等腰三角形时,求AP的长.
参考答案
一、选择题:(本大题共6题,每题2分,满分12分)
1.下列二次根式中,与属同类二次根式的是( )
A. B. C. D.
【分析】各式化简为最简二次根式,找出被开方数相同的即为同类二次根式.
解:A、原式=3,不符合题意;
B、原式=3|a|,不符合题意;
C、原式=3|b|,不符合题意;
D、原式=3|b|,符合题意.
故选:D.
2.下列各数中,是方程2x2+5x=3的根的是( )
A.﹣3 B.﹣1 C.1 D.3
【分析】求出一元二次方程的解,再判断即可.
解:2x2+5x﹣3=0,
(2x﹣1)(x+3)=0,
2x﹣1=0,x+3=0,
x1=,x2=﹣3.
故选:A.
3.直线y=﹣x不经过点( )
A.(0,0) B.(﹣2,3) C.(3,﹣2) D.(﹣3,2)
【分析】直接把各点代入直线y=﹣x进行检验即可.
解:A、当x=0时,y=﹣×0=0,故此点在直线上,故本选项错误;
B、当x=﹣2时,y=﹣×(﹣2)=≠3,故此点不在直线上,故本选项正确;
C、当x=3时,y=﹣×3=﹣2,故此点在直线上,故本选项错误;
D、当x=﹣3时,y=﹣×(﹣3)=2,故此点在直线上,故本选项错误.
故选:B.
4.用下列几组边长构成的三角形中哪一组不是直角三角形( )
A.8,15,17 B.,, C.,2, D.1,2,
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.
解:A、∵82+152=172,∴此三角形为直角三角形,故选项错误;
B、∵()2+()2=()2,∴此三角形是直角三角形,故选项错误;
C、∵()2+22≠()2,∴此三角形不是直角三角形,故选项正确;
D、∵12+22=()2,∴此三角形为直角三角形,故选项错误.
故选:C.
5.下列命题中,逆命题是假命题的是( )
A.两直线平行,同旁内角互补
B.直角三角形的两个锐角互余
C.全等三角形的对应角相等
D.直角三角形两条直角边的平方和等于斜边的平方
【分析】交换原命题的逆命题后判断正误即可.
解:A、逆命题为:同旁内角互补,两直线平行,正确,是真命题,不符合题意;
B、逆命题为:两个锐角互余的三角形是直角三角形,正确,是真命题,不符合题意;
C、逆命题为:对应角相等的三角形全等,错误,是假命题,符合题意;
D、逆命题为:两条边的平方和等于第三边的平方的三角形是直角三角形,正确,是真命题,不符合题意.
故选:C.
6.已知在△ABC中,AB=2,AC=2,BC边上的高等于,那么BC的长是 ( )
A.2 B.4 C.2或4 D.无法确定.
【分析】根据勾股定理分别求出BD,CD,结合图形计算即可.
解:BD==3,
CD==1,
如图(1)BC=BD+CD=4,
如图2,BC=BD﹣CD=2,
故选:C.
二、填空题:(本大题共12题,每题3分,满分36分)
7.的有理化因式是 (答案不唯一) .
【分析】找出已知二次根式的有理化因式即可.
解:的有理化因式是(答案不唯一).
故答案为:(答案不唯一).
8.函数的定义域是 .
【分析】根据二次根式的性质,被开方数大于或等于0,可知:2x﹣3≥0,解得x的范围.
解:要使函数有意义,
则2x﹣3≥0,
解得x.
故答案为x≥.
9.在实数范围内分解因式:2x2﹣3x﹣1= 2(x﹣﹣)(x﹣+) .
【分析】解方程2x2﹣3x﹣1=0得,x1=,x2=,则可将该多项式实现实数范围内的因式分解.
解:解方程2x2﹣3x﹣1=0得,
x1=,x2=,
则2x2﹣3x﹣1=2(x﹣)(x﹣)=2(x﹣﹣)(x﹣+).
10.已知关于x的一元二次方程mx2﹣2x+1=0有两个不相等的实数根,那么m的取值范围是 m<1且m≠0 .
【分析】根据二次项系数非零及根的判别式Δ>0,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围.
解:∵关于x的一元二次方程mx2﹣2x+1=0有两个不相等的实数根,
∴,
解得:m<1且m≠0.
故答案为:m<1且m≠0.
11.已知函数f(x)=,那么f(2)= 1 .
【分析】把x=2代入函数关系式计算即可.
解:当x=2时,f(2)===1.
故答案为:1.
12.我们学校响应国家对垃圾分类处理的号召,组织同学们积极学习垃圾分类相关知识.初二年级某班每月进行一次垃圾分类知识测试,结果显示9月份32名同学测试结果优秀,到11月份增加到38名同学测试结果优秀,设平均每月优秀人数增长的百分率为x,则可以列出的方程是 32(1+x)2=38 .
【分析】如果设平均每月优秀人数增长的百分率是x,那么10月份的优秀人数是32(1+x)人, 11月份的优秀人数是32(1+x)2元,而此时优秀人数是38人,列出方程.
解:设平均每月优秀人数增长的百分率是x,依题意,得
32(1+x)2=38.
故答案为:32(1+x)2=38.
13.已知P(x1,y1),Q(x2,y2)在反比例函数的图象上,若x1<x2<0,则y1 > y2
(填“>”“<”或“=”).
【分析】根据反比例函数的比例系数k>0可知,该函数在x<0内单调递减,再结合x1<x2<0,即可得出结论.
解:∵反比例函数中k>0,
∴该函数在x<0内单调递减.
∵x1<x2<0,
∴y1>y2.
故答案为:>.
14.如果点A的坐标为(2,﹣1),点B的坐标为(5,3),那么A、B两点的距离等于 5 .
【分析】根据两点间的距离公式计算即可.
解:由两点间的距离公式得,AB==5,
故答案为:5.
15.到点P的距离等于5的点的轨迹是 以点P为圆心,5为半径的圆 .
【分析】根据圆的定义即可得出答案.
解:根据圆的定义可知:到点P的距离等于5的点的轨迹是以点P为圆心,5为半径的圆,
故答案为:以点P为圆心,5为半径的圆.
16.在△ABC中,AB=10,BC=8,∠B=60°,则AC的长度是 2 .
【分析】根据题意画出图形,结合锐角三角函数关系以及勾股定理得出AD,AC的长即可.
解:如图所示:过点A作AD⊥BC于点D,
∵AB=10,∠B=60°,∠BDA=90°,
∴BD=AB=5,
∴CD=3,AD=,
∴在Rt△ADC中,AC=.
故答案为:2.
17.如图,点P是∠AOB的角平分线上的一点,过点P作PC∥OA交OB于点C,PD⊥OA,若∠AOB=60°,OC=2,则PD= .
【分析】过P点作PH⊥OB于H,如图,先利用角平分线的性质得到∠POD=∠POC,PD=PH,再利用平行线的性质证明∠CPO=∠POC得到PC=OC=2,然后利用含30度的直角三角形三边的关系.
解:过P点作PH⊥OB于H,如图,
∵OP平分∠AOB,PD⊥OA,PH⊥OB,
∴∠POD=∠POC,PD=PH,
∵PC∥OA,
∴∠POD=∠CPO,∠PCH=∠AOB=60°,
∴∠CPO=∠POC,
∴PC=OC=2,
在Rt△PCH中,∴∠PCH=60°,
∴CH=PC=1,
∴PH=CH=,
∴PD=.
故答案为:.
18.如图,将长方形ABCD绕点A顺时针旋转,点D落在边BC上的点D′处,点B、C分别落在点B′、点C′处,如果∠D′BC′=∠D′C′B,那么DC:D′C的比值等于 +1 .
【分析】根据题意可作出图形,由旋转可知,DC=D′C′,AD=AD′,因为∠D′BC′=∠D′C′B,所以BD′=C′D′=AB=CD,所以△ABD′是等腰直角三角形,则AD′=BC=AB=DC,所以DC:D′C=DC:(BC﹣BD′)=DA:(DC﹣DC)=+1.
解:根据题意可作出图形,
由旋转可知,DC=D′C′,AD=AD′,
∵∠D′BC′=∠D′C′B,
∴BD′=C′D′,
又∵AB=CD,
∴AB=BD′=DC,
∴△ABD′是等腰直角三角形,
∴AD′=AB=DC,
∴BC=DC,
∴DC:D′C=DC:(BC﹣BD′)=DA:(DC﹣DC)=+1.
故答案为:+1.
三、简答题:(本大题共4题,每题6分,满分24分)
19.计算:.
【分析】先进行分母有理化,再化简二次根式,最后合并即可.
解:原式=5﹣(﹣)+5
=5﹣++5
=4+6.
20.解方程:(x2﹣9)+x(x﹣3)=0.
【分析】先把方程化为一般式,然后利用求根公式解方程.
解:(x2﹣9)+x(x﹣3)=0,
由原方程,得2x2﹣3x﹣9=0,
则a=2,b=﹣3,c=﹣9,
△=(﹣3)2﹣4×2×(﹣9)=81>0,
x==,
所以x1==3,x2==﹣,
∴x1=3,x2=﹣.
21.已知y=y1+y2,y1与x﹣1成正比例,y2与x成反比例,且当x=2时,y=1;当x=﹣2时,y=﹣2,求y关于x的函数解析式.
【分析】可设y1=k1(x﹣1),y2=(k1≠0,k2≠0),把已知条件代入则可求得y与x的函数解析式;
解:设y1=k1(x﹣1),y2=(k1≠0,k2≠0),
∴y=y1+y2=k1(x﹣1)+.
把x=2时,y=1;当x=﹣2时,y=﹣2代入可得:,
解得,,
∴y关于x的函数解析式为y=(x﹣1)+.
22.一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用的时间为t(小时),航行的路程为s(千米),s与t的函数图象如图所示.
(1)甲乙两地相距 60 千米;
(2)轮船顺水航行时航行的路程s关于所用时间t的函数关系式为 s=30t ,定义域是 0≤t≤2 ;
(3)如果轮船从乙地逆水航行返回到甲地时的速度为20千米/小时,那么点M的坐标是 (11,120) .
【分析】(1)从图象直接观察即可;
(2)根据图象用待定系数法求函数解析式即可;
(3)根据顺水航行的路程与逆水航行的路程相等求出纵坐标,再根据路程÷速度=时间求出时间,再加上8即可得出横坐标.
解:(1)由图象可知:甲乙两地相距60千米,
故答案为:60;
(2)设轮船顺水航行时航行的路程s关于所用时间t的函数关系式为s=kt,
把(2,60)代入,得2k=60,
解得:k=30,
则轮船顺水航行时航行的路程s关于所用时间t的函数关系式为s=30t,
其中0<≤t≤2,
故答案为:s=30t,0<≤t≤2;
(3)由题意得:60÷20=3(小时),
则点M的横坐标为8+3=11,
纵坐标为60×2=120,
故点M的坐标为(11,120).
故答案为:(11,120).
四、解答题:(本大题共4题,第23、24题每题6分,第25、26题每题8分,满分28分)
23.已知,如图,在△ABC中,∠B=60°,BC=4.
(1)尺规作图:求作一点P,使点P到点B、C的距离相等,同时P到边BA、BC的距离相等(不写作法,保留作图痕迹);
(2)求出点P到点B的距离.
【分析】(1)作∠ABC的角平分线BQ,作线段BC的垂直平分线MN,MN交BC于点DM交BQ于点P,点P即为所求;
(2)解直角三角形求出BP即可.
解:(1)如图,点P即为所求;
(2)∵BQ平分∠ABC,
∴∠ABC=∠ABC=30°,
∵MN垂直平分线段BC,
∴BD=CD=2,
∴PB===.
24.已知:如图,在△ABC中,AD是BC边上的高,CE是中线,F是CE的中点,CD=AB,求证:DF⊥CE.
【分析】连接DE,根据直角三角形斜边上的中线等于斜边的一半可得DE=AB,再求出DE=CD,然后根据等腰三角形三线合一的性质证明即可.
【解答】证明:连接DE,
∵AD是BC边上的高,在Rt△ADB中,CE是中线,
∴DE=AB,
∵CD=AB,
∴DC=DE,
∵F是CE中点,
∴DF⊥CE.
25.如图,直线y=ax(a>0)与双曲线y=(k>0)交于A、B两点,且点A的坐标为(4,2),点B的坐标为(n,﹣2).
(1)求a,n的值;
(2)若双曲线y=(k>0)的上点C的纵坐标为8,求△AOC的面积.
【分析】(1)根据待定系数法即可求得a的值,根据一次函数图象上点的坐标特征即可求得n;
(2)由条件(1)知,k=8,点C的纵坐标为8,求出C的坐标为(1,8),然后根据S△AOC=S△COD+S梯形ACDE﹣S△AOE=S梯形ACDE即可求得.
解:(1)∵直线y=ax(a>0)与双曲线y=(k>0)交于A、B两点,
∴,
解得a=,n=﹣4;
(2)∵双曲线y=(k>0)经过A点,
∴k=4×2=8,
∵双曲线y=(k>0)的上点C的纵坐标为8,
∴C点的坐标为(1,8),
如图,作AE⊥x轴于E,CD⊥x轴于D,
∴S△AOC=S△COD+S梯形ACDE﹣S△AOE=S梯形ACDE=(8+2)(4﹣1)=15.
26.已知:如图,在△ABC纸片中,AC=3,BC=4,AB=5,按图所示的方法将△ACD沿AD折叠,使点C恰好落在边AB上的点C′处,点P是射线AB上的一个动点.
(1)求折痕AD长.
(2)点P在线段AB上运动时,设AP=x,DP=y.求y关于x的函数解析式,并写出此函数的定义域.
(3)当△APD是等腰三角形时,求AP的长.
【分析】(1)由翻折可知:CD=DC′,AC=AC′=3,设CD=DC′=x,在Rt△BDC中,根据BD2=C′D2+C′B2,构建方程即可解决问题.
(2)利用勾股定理即可解决问题.
(3)分三种情形:①PA=PD,②AP=AD,③当PD=AD时,分别求解即可.
解:(1)如图1中,
由翻折可知:CD=DC′,AC=AC′=3,设CD=DC′=x,
在Rt△BDC中,∵BD2=C′D2+C′B2,
∴(4﹣x)2=x2+22,
解得x=,
∴AD===.
(2)如图2中,当点P在C'D左侧,AC=AC'=3,则PC'=3﹣x,
∵,
∴y==(0≤x≤10).
当点P在C'D右侧,同理可得y=(0≤x≤10).
∴y关于x的函数解析式为y=(0≤x≤10).
(3)如图3中,
①当PA=PD时,设PA=PD=m,
在Rt△PCD中,∵PD2=DC′2+C′P2,
∴m2=()2+(3﹣m)2,
解得m=,
∴PA=.
②当AD=AP′=时,△ADP′是等腰三角形,
③当PD=AD时,点P在AB的延长线上.如图4,
AP=2AC'=6.
综上所述,满足条件的PA的值为或或6.
一、选择题(共6题,每题2分,满分12分)
1.下列二次根式中,与属同类二次根式的是( )
A. B. C. D.
2.下列各数中,是方程2x2+5x=3的根的是( )
A.﹣3 B.﹣1 C.1 D.3
3.直线y=﹣x不经过点( )
A.(0,0) B.(﹣2,3) C.(3,﹣2) D.(﹣3,2)
4.用下列几组边长构成的三角形中哪一组不是直角三角形( )
A.8,15,17 B.,, C.,2, D.1,2,
5.下列命题中,逆命题是假命题的是( )
A.两直线平行,同旁内角互补
B.直角三角形的两个锐角互余
C.全等三角形的对应角相等
D.直角三角形两条直角边的平方和等于斜边的平方
6.已知在△ABC中,AB=2,AC=2,BC边上的高等于,那么BC的长是 ( )
A.2 B.4 C.2或4 D.无法确定.
二、填空题:(本大题共12题,每题3分,满分36分)
7.的有理化因式是 .
8.函数的定义域是 .
9.在实数范围内分解因式:2x2﹣3x﹣1= .
10.已知关于x的一元二次方程mx2﹣2x+1=0有两个不相等的实数根,那么m的取值范围是 .
11.已知函数f(x)=,那么f(2)= .
12.我们学校响应国家对垃圾分类处理的号召,组织同学们积极学习垃圾分类相关知识.初二年级某班每月进行一次垃圾分类知识测试,结果显示9月份32名同学测试结果优秀,到11月份增加到38名同学测试结果优秀,设平均每月优秀人数增长的百分率为x,则可以列出的方程是 .
13.已知P(x1,y1),Q(x2,y2)在反比例函数的图象上,若x1<x2<0,则y1 y2
(填“>”“<”或“=”).
14.如果点A的坐标为(2,﹣1),点B的坐标为(5,3),那么A、B两点的距离等于 .
15.到点P的距离等于5的点的轨迹是 .
16.在△ABC中,AB=10,BC=8,∠B=60°,则AC的长度是 .
17.如图,点P是∠AOB的角平分线上的一点,过点P作PC∥OA交OB于点C,PD⊥OA,若∠AOB=60°,OC=2,则PD= .
18.如图,将长方形ABCD绕点A顺时针旋转,点D落在边BC上的点D′处,点B、C分别落在点B′、点C′处,如果∠D′BC′=∠D′C′B,那么DC:D′C的比值等于 .
三、简答题:(本大题共4题,每题6分,满分24分)
19.计算:.
20.解方程:(x2﹣9)+x(x﹣3)=0.
21.已知y=y1+y2,y1与x﹣1成正比例,y2与x成反比例,且当x=2时,y=1;当x=﹣2时,y=﹣2,求y关于x的函数解析式.
22.一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用的时间为t(小时),航行的路程为s(千米),s与t的函数图象如图所示.
(1)甲乙两地相距 千米;
(2)轮船顺水航行时航行的路程s关于所用时间t的函数关系式为 ,定义域是 ;
(3)如果轮船从乙地逆水航行返回到甲地时的速度为20千米/小时,那么点M的坐标是 .
四、解答题:(本大题共4题,第23、24题每题6分,第25、26题每题8分,满分28分)
23.已知,如图,在△ABC中,∠B=60°,BC=4.
(1)尺规作图:求作一点P,使点P到点B、C的距离相等,同时P到边BA、BC的距离相等(不写作法,保留作图痕迹);
(2)求出点P到点B的距离.
24.已知:如图,在△ABC中,AD是BC边上的高,CE是中线,F是CE的中点,CD=AB,求证:DF⊥CE.
25.如图,直线y=ax(a>0)与双曲线y=(k>0)交于A、B两点,且点A的坐标为(4,2),点B的坐标为(n,﹣2).
(1)求a,n的值;
(2)若双曲线y=(k>0)的上点C的纵坐标为8,求△AOC的面积.
26.已知:如图,在△ABC纸片中,AC=3,BC=4,AB=5,按图所示的方法将△ACD沿AD折叠,使点C恰好落在边AB上的点C′处,点P是射线AB上的一个动点.
(1)求折痕AD长.
(2)点P在线段AB上运动时,设AP=x,DP=y.求y关于x的函数解析式,并写出此函数的定义域.
(3)当△APD是等腰三角形时,求AP的长.
参考答案
一、选择题:(本大题共6题,每题2分,满分12分)
1.下列二次根式中,与属同类二次根式的是( )
A. B. C. D.
【分析】各式化简为最简二次根式,找出被开方数相同的即为同类二次根式.
解:A、原式=3,不符合题意;
B、原式=3|a|,不符合题意;
C、原式=3|b|,不符合题意;
D、原式=3|b|,符合题意.
故选:D.
2.下列各数中,是方程2x2+5x=3的根的是( )
A.﹣3 B.﹣1 C.1 D.3
【分析】求出一元二次方程的解,再判断即可.
解:2x2+5x﹣3=0,
(2x﹣1)(x+3)=0,
2x﹣1=0,x+3=0,
x1=,x2=﹣3.
故选:A.
3.直线y=﹣x不经过点( )
A.(0,0) B.(﹣2,3) C.(3,﹣2) D.(﹣3,2)
【分析】直接把各点代入直线y=﹣x进行检验即可.
解:A、当x=0时,y=﹣×0=0,故此点在直线上,故本选项错误;
B、当x=﹣2时,y=﹣×(﹣2)=≠3,故此点不在直线上,故本选项正确;
C、当x=3时,y=﹣×3=﹣2,故此点在直线上,故本选项错误;
D、当x=﹣3时,y=﹣×(﹣3)=2,故此点在直线上,故本选项错误.
故选:B.
4.用下列几组边长构成的三角形中哪一组不是直角三角形( )
A.8,15,17 B.,, C.,2, D.1,2,
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.
解:A、∵82+152=172,∴此三角形为直角三角形,故选项错误;
B、∵()2+()2=()2,∴此三角形是直角三角形,故选项错误;
C、∵()2+22≠()2,∴此三角形不是直角三角形,故选项正确;
D、∵12+22=()2,∴此三角形为直角三角形,故选项错误.
故选:C.
5.下列命题中,逆命题是假命题的是( )
A.两直线平行,同旁内角互补
B.直角三角形的两个锐角互余
C.全等三角形的对应角相等
D.直角三角形两条直角边的平方和等于斜边的平方
【分析】交换原命题的逆命题后判断正误即可.
解:A、逆命题为:同旁内角互补,两直线平行,正确,是真命题,不符合题意;
B、逆命题为:两个锐角互余的三角形是直角三角形,正确,是真命题,不符合题意;
C、逆命题为:对应角相等的三角形全等,错误,是假命题,符合题意;
D、逆命题为:两条边的平方和等于第三边的平方的三角形是直角三角形,正确,是真命题,不符合题意.
故选:C.
6.已知在△ABC中,AB=2,AC=2,BC边上的高等于,那么BC的长是 ( )
A.2 B.4 C.2或4 D.无法确定.
【分析】根据勾股定理分别求出BD,CD,结合图形计算即可.
解:BD==3,
CD==1,
如图(1)BC=BD+CD=4,
如图2,BC=BD﹣CD=2,
故选:C.
二、填空题:(本大题共12题,每题3分,满分36分)
7.的有理化因式是 (答案不唯一) .
【分析】找出已知二次根式的有理化因式即可.
解:的有理化因式是(答案不唯一).
故答案为:(答案不唯一).
8.函数的定义域是 .
【分析】根据二次根式的性质,被开方数大于或等于0,可知:2x﹣3≥0,解得x的范围.
解:要使函数有意义,
则2x﹣3≥0,
解得x.
故答案为x≥.
9.在实数范围内分解因式:2x2﹣3x﹣1= 2(x﹣﹣)(x﹣+) .
【分析】解方程2x2﹣3x﹣1=0得,x1=,x2=,则可将该多项式实现实数范围内的因式分解.
解:解方程2x2﹣3x﹣1=0得,
x1=,x2=,
则2x2﹣3x﹣1=2(x﹣)(x﹣)=2(x﹣﹣)(x﹣+).
10.已知关于x的一元二次方程mx2﹣2x+1=0有两个不相等的实数根,那么m的取值范围是 m<1且m≠0 .
【分析】根据二次项系数非零及根的判别式Δ>0,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围.
解:∵关于x的一元二次方程mx2﹣2x+1=0有两个不相等的实数根,
∴,
解得:m<1且m≠0.
故答案为:m<1且m≠0.
11.已知函数f(x)=,那么f(2)= 1 .
【分析】把x=2代入函数关系式计算即可.
解:当x=2时,f(2)===1.
故答案为:1.
12.我们学校响应国家对垃圾分类处理的号召,组织同学们积极学习垃圾分类相关知识.初二年级某班每月进行一次垃圾分类知识测试,结果显示9月份32名同学测试结果优秀,到11月份增加到38名同学测试结果优秀,设平均每月优秀人数增长的百分率为x,则可以列出的方程是 32(1+x)2=38 .
【分析】如果设平均每月优秀人数增长的百分率是x,那么10月份的优秀人数是32(1+x)人, 11月份的优秀人数是32(1+x)2元,而此时优秀人数是38人,列出方程.
解:设平均每月优秀人数增长的百分率是x,依题意,得
32(1+x)2=38.
故答案为:32(1+x)2=38.
13.已知P(x1,y1),Q(x2,y2)在反比例函数的图象上,若x1<x2<0,则y1 > y2
(填“>”“<”或“=”).
【分析】根据反比例函数的比例系数k>0可知,该函数在x<0内单调递减,再结合x1<x2<0,即可得出结论.
解:∵反比例函数中k>0,
∴该函数在x<0内单调递减.
∵x1<x2<0,
∴y1>y2.
故答案为:>.
14.如果点A的坐标为(2,﹣1),点B的坐标为(5,3),那么A、B两点的距离等于 5 .
【分析】根据两点间的距离公式计算即可.
解:由两点间的距离公式得,AB==5,
故答案为:5.
15.到点P的距离等于5的点的轨迹是 以点P为圆心,5为半径的圆 .
【分析】根据圆的定义即可得出答案.
解:根据圆的定义可知:到点P的距离等于5的点的轨迹是以点P为圆心,5为半径的圆,
故答案为:以点P为圆心,5为半径的圆.
16.在△ABC中,AB=10,BC=8,∠B=60°,则AC的长度是 2 .
【分析】根据题意画出图形,结合锐角三角函数关系以及勾股定理得出AD,AC的长即可.
解:如图所示:过点A作AD⊥BC于点D,
∵AB=10,∠B=60°,∠BDA=90°,
∴BD=AB=5,
∴CD=3,AD=,
∴在Rt△ADC中,AC=.
故答案为:2.
17.如图,点P是∠AOB的角平分线上的一点,过点P作PC∥OA交OB于点C,PD⊥OA,若∠AOB=60°,OC=2,则PD= .
【分析】过P点作PH⊥OB于H,如图,先利用角平分线的性质得到∠POD=∠POC,PD=PH,再利用平行线的性质证明∠CPO=∠POC得到PC=OC=2,然后利用含30度的直角三角形三边的关系.
解:过P点作PH⊥OB于H,如图,
∵OP平分∠AOB,PD⊥OA,PH⊥OB,
∴∠POD=∠POC,PD=PH,
∵PC∥OA,
∴∠POD=∠CPO,∠PCH=∠AOB=60°,
∴∠CPO=∠POC,
∴PC=OC=2,
在Rt△PCH中,∴∠PCH=60°,
∴CH=PC=1,
∴PH=CH=,
∴PD=.
故答案为:.
18.如图,将长方形ABCD绕点A顺时针旋转,点D落在边BC上的点D′处,点B、C分别落在点B′、点C′处,如果∠D′BC′=∠D′C′B,那么DC:D′C的比值等于 +1 .
【分析】根据题意可作出图形,由旋转可知,DC=D′C′,AD=AD′,因为∠D′BC′=∠D′C′B,所以BD′=C′D′=AB=CD,所以△ABD′是等腰直角三角形,则AD′=BC=AB=DC,所以DC:D′C=DC:(BC﹣BD′)=DA:(DC﹣DC)=+1.
解:根据题意可作出图形,
由旋转可知,DC=D′C′,AD=AD′,
∵∠D′BC′=∠D′C′B,
∴BD′=C′D′,
又∵AB=CD,
∴AB=BD′=DC,
∴△ABD′是等腰直角三角形,
∴AD′=AB=DC,
∴BC=DC,
∴DC:D′C=DC:(BC﹣BD′)=DA:(DC﹣DC)=+1.
故答案为:+1.
三、简答题:(本大题共4题,每题6分,满分24分)
19.计算:.
【分析】先进行分母有理化,再化简二次根式,最后合并即可.
解:原式=5﹣(﹣)+5
=5﹣++5
=4+6.
20.解方程:(x2﹣9)+x(x﹣3)=0.
【分析】先把方程化为一般式,然后利用求根公式解方程.
解:(x2﹣9)+x(x﹣3)=0,
由原方程,得2x2﹣3x﹣9=0,
则a=2,b=﹣3,c=﹣9,
△=(﹣3)2﹣4×2×(﹣9)=81>0,
x==,
所以x1==3,x2==﹣,
∴x1=3,x2=﹣.
21.已知y=y1+y2,y1与x﹣1成正比例,y2与x成反比例,且当x=2时,y=1;当x=﹣2时,y=﹣2,求y关于x的函数解析式.
【分析】可设y1=k1(x﹣1),y2=(k1≠0,k2≠0),把已知条件代入则可求得y与x的函数解析式;
解:设y1=k1(x﹣1),y2=(k1≠0,k2≠0),
∴y=y1+y2=k1(x﹣1)+.
把x=2时,y=1;当x=﹣2时,y=﹣2代入可得:,
解得,,
∴y关于x的函数解析式为y=(x﹣1)+.
22.一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用的时间为t(小时),航行的路程为s(千米),s与t的函数图象如图所示.
(1)甲乙两地相距 60 千米;
(2)轮船顺水航行时航行的路程s关于所用时间t的函数关系式为 s=30t ,定义域是 0≤t≤2 ;
(3)如果轮船从乙地逆水航行返回到甲地时的速度为20千米/小时,那么点M的坐标是 (11,120) .
【分析】(1)从图象直接观察即可;
(2)根据图象用待定系数法求函数解析式即可;
(3)根据顺水航行的路程与逆水航行的路程相等求出纵坐标,再根据路程÷速度=时间求出时间,再加上8即可得出横坐标.
解:(1)由图象可知:甲乙两地相距60千米,
故答案为:60;
(2)设轮船顺水航行时航行的路程s关于所用时间t的函数关系式为s=kt,
把(2,60)代入,得2k=60,
解得:k=30,
则轮船顺水航行时航行的路程s关于所用时间t的函数关系式为s=30t,
其中0<≤t≤2,
故答案为:s=30t,0<≤t≤2;
(3)由题意得:60÷20=3(小时),
则点M的横坐标为8+3=11,
纵坐标为60×2=120,
故点M的坐标为(11,120).
故答案为:(11,120).
四、解答题:(本大题共4题,第23、24题每题6分,第25、26题每题8分,满分28分)
23.已知,如图,在△ABC中,∠B=60°,BC=4.
(1)尺规作图:求作一点P,使点P到点B、C的距离相等,同时P到边BA、BC的距离相等(不写作法,保留作图痕迹);
(2)求出点P到点B的距离.
【分析】(1)作∠ABC的角平分线BQ,作线段BC的垂直平分线MN,MN交BC于点DM交BQ于点P,点P即为所求;
(2)解直角三角形求出BP即可.
解:(1)如图,点P即为所求;
(2)∵BQ平分∠ABC,
∴∠ABC=∠ABC=30°,
∵MN垂直平分线段BC,
∴BD=CD=2,
∴PB===.
24.已知:如图,在△ABC中,AD是BC边上的高,CE是中线,F是CE的中点,CD=AB,求证:DF⊥CE.
【分析】连接DE,根据直角三角形斜边上的中线等于斜边的一半可得DE=AB,再求出DE=CD,然后根据等腰三角形三线合一的性质证明即可.
【解答】证明:连接DE,
∵AD是BC边上的高,在Rt△ADB中,CE是中线,
∴DE=AB,
∵CD=AB,
∴DC=DE,
∵F是CE中点,
∴DF⊥CE.
25.如图,直线y=ax(a>0)与双曲线y=(k>0)交于A、B两点,且点A的坐标为(4,2),点B的坐标为(n,﹣2).
(1)求a,n的值;
(2)若双曲线y=(k>0)的上点C的纵坐标为8,求△AOC的面积.
【分析】(1)根据待定系数法即可求得a的值,根据一次函数图象上点的坐标特征即可求得n;
(2)由条件(1)知,k=8,点C的纵坐标为8,求出C的坐标为(1,8),然后根据S△AOC=S△COD+S梯形ACDE﹣S△AOE=S梯形ACDE即可求得.
解:(1)∵直线y=ax(a>0)与双曲线y=(k>0)交于A、B两点,
∴,
解得a=,n=﹣4;
(2)∵双曲线y=(k>0)经过A点,
∴k=4×2=8,
∵双曲线y=(k>0)的上点C的纵坐标为8,
∴C点的坐标为(1,8),
如图,作AE⊥x轴于E,CD⊥x轴于D,
∴S△AOC=S△COD+S梯形ACDE﹣S△AOE=S梯形ACDE=(8+2)(4﹣1)=15.
26.已知:如图,在△ABC纸片中,AC=3,BC=4,AB=5,按图所示的方法将△ACD沿AD折叠,使点C恰好落在边AB上的点C′处,点P是射线AB上的一个动点.
(1)求折痕AD长.
(2)点P在线段AB上运动时,设AP=x,DP=y.求y关于x的函数解析式,并写出此函数的定义域.
(3)当△APD是等腰三角形时,求AP的长.
【分析】(1)由翻折可知:CD=DC′,AC=AC′=3,设CD=DC′=x,在Rt△BDC中,根据BD2=C′D2+C′B2,构建方程即可解决问题.
(2)利用勾股定理即可解决问题.
(3)分三种情形:①PA=PD,②AP=AD,③当PD=AD时,分别求解即可.
解:(1)如图1中,
由翻折可知:CD=DC′,AC=AC′=3,设CD=DC′=x,
在Rt△BDC中,∵BD2=C′D2+C′B2,
∴(4﹣x)2=x2+22,
解得x=,
∴AD===.
(2)如图2中,当点P在C'D左侧,AC=AC'=3,则PC'=3﹣x,
∵,
∴y==(0≤x≤10).
当点P在C'D右侧,同理可得y=(0≤x≤10).
∴y关于x的函数解析式为y=(0≤x≤10).
(3)如图3中,
①当PA=PD时,设PA=PD=m,
在Rt△PCD中,∵PD2=DC′2+C′P2,
∴m2=()2+(3﹣m)2,
解得m=,
∴PA=.
②当AD=AP′=时,△ADP′是等腰三角形,
③当PD=AD时,点P在AB的延长线上.如图4,
AP=2AC'=6.
综上所述,满足条件的PA的值为或或6.
同课章节目录
