人教版八年级数学下册17.1第2课时勾股定理在实际生活中的应用 课件(共24张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.1第2课时勾股定理在实际生活中的应用 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 08:54:52 | ||
图片预览




文档简介
(共24张PPT)
第十七章
17.1勾股定理
第二课时
勾股定理在实际生活中的应用
人教版数学 八年级下册
学习目标
能运用勾股定理及直角三角形的判定条件解决实际问题.
能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
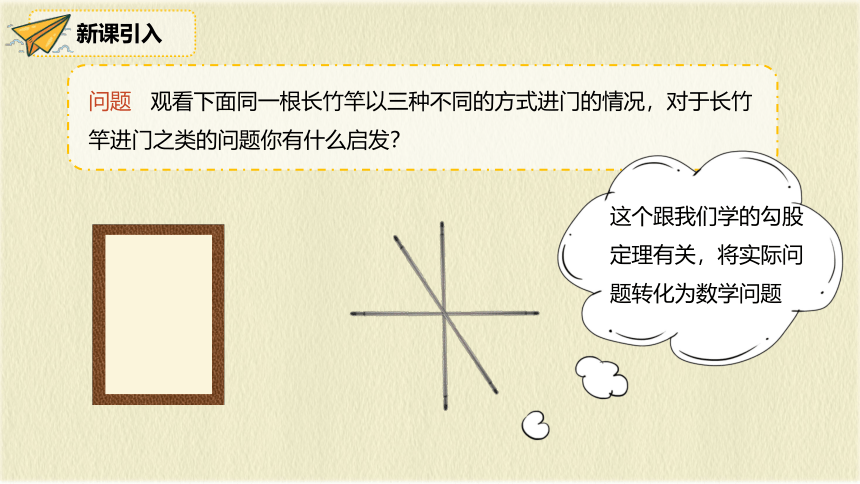
问题 观看下面同一根长竹竿以三种不同的方式进门的情况,对于长竹竿进门之类的问题你有什么启发?
这个跟我们学的勾股定理有关,将实际问题转化为数学问题
新课引入
新知讲解
例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过 为什么
2m
1m
A
B
D
C
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
分析:可以看出木板横着,竖着都不能通过,只能斜着.门框AC的长度是斜着能通过的最大长度,只要AC的长大于木板的宽就能通过.
新知讲解
A
B
D
C
O
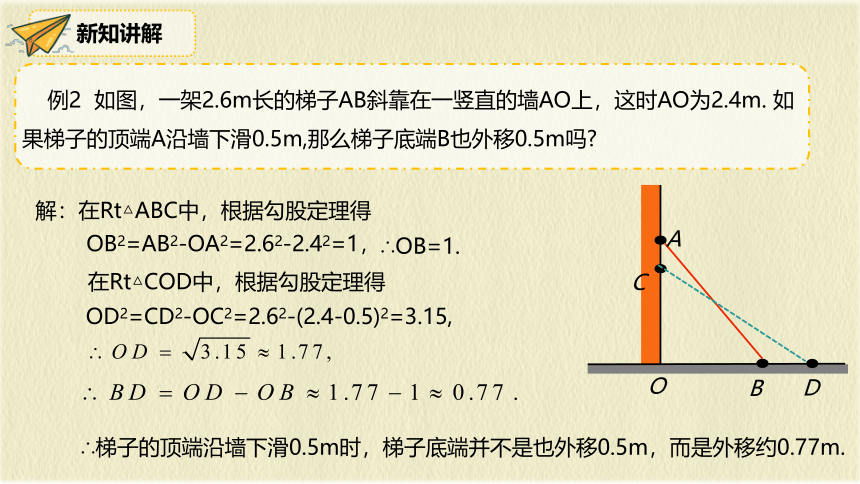
解:在Rt△ABC中,根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1,
∴OB=1.
在Rt△COD中,根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
例2 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
新知讲解
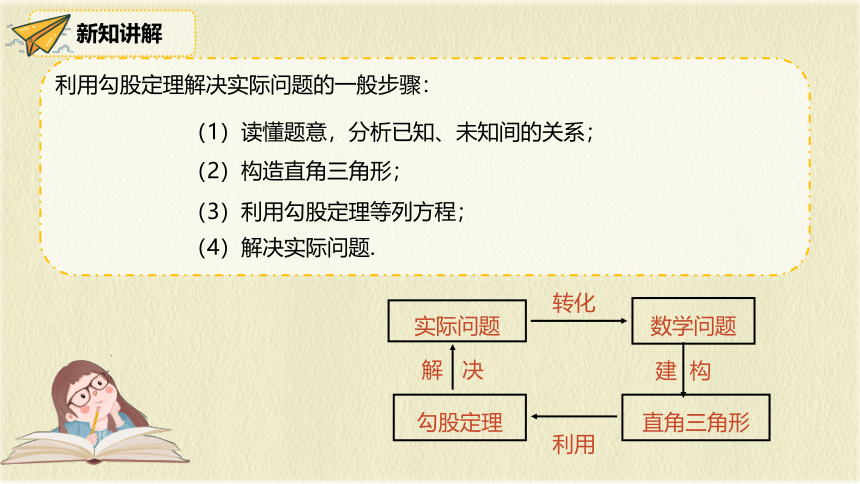
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
建 构
利用
解 决
新知讲解
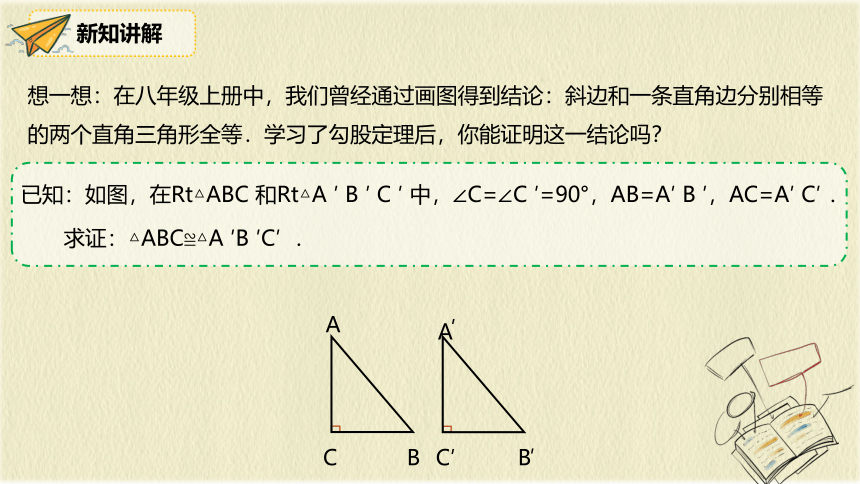
想一想:在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A ′ B ′ C ′ 中,∠C=∠C ′=90°,AB=A′ B ′,AC=A′ C′ .
求证:△ABC≌△A ′B ′C′ .
A
B
C
A
B
C′
′
′
新知讲解
证明:在Rt△ABC 和Rt△A ′B ′C ′中,∠C=∠C′=90°,
根据勾股定理得
A
B
C
A
B
C′
′
′
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
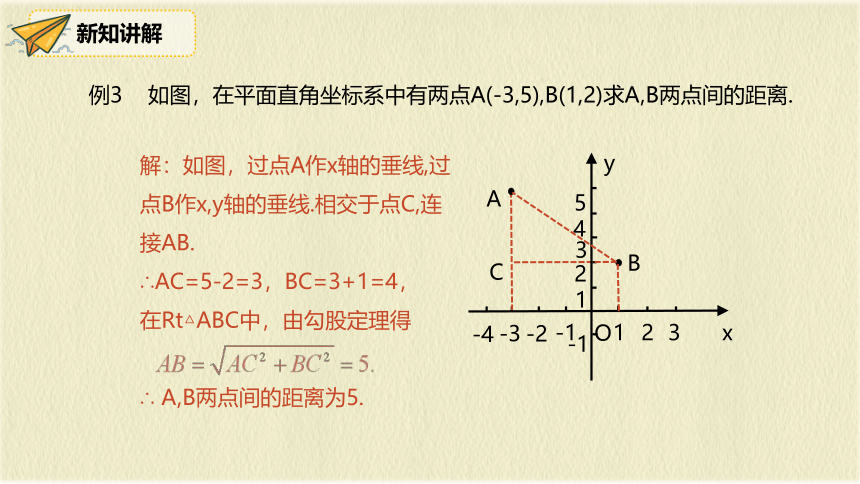
例3 如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
y
O
x
3
B
C
解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴ A,B两点间的距离为5.
新知讲解
新知讲解
方法总结:
两点之间的距离公式:
一般地,设平面上任意两点
C
B
A
问题 在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B 路线,难道小狗也懂数学?
AC+CB >AB(两点之间线段最短)
思考:在立体图形中,怎么寻找最短线路呢?
新知讲解
A
B
A'
A
B
B
A
O
想一想:蚂蚁走哪一条路线最近?
蚂蚁A→B的路线
问题:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想沿侧面从A处爬向B处,蚂蚁怎么走最近?
B
A
根据两点之间线段最短易知第三个路线最近.
新知讲解
若已知圆柱体高为12 cm,底面半径为3 cm,π取3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在Rt△ABA′中,由勾股定理得
新知讲解
立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
新知讲解
例4 有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2 m,高AB是5 m,π取3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,
∴AB'=13. 即梯子最短需13米.
新知讲解
数学思想:
立体图形
平面图形
转化
展开
新知讲解
B
牛奶盒
A
【变式题】看到小蚂蚁终于喝到饮料的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程么?
6cm
8cm
10cm
例5 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
牧童A
小屋B
A′
C
东
北
解:如图,作出点A关于河岸的对称点A′,连接A′B则A′B就是最短路线.
由题意得A′C=4+4+7=15(km),BC=8km.
在Rt△A′CB中,由勾股定理得
新知讲解
新知讲解
求直线同侧的两点到直线上一点所连线段的和的最短路径的方法:先找到其中一点关于这条直线的对称点,连接对称点与另一点的线段就是最短路径长,以连接对称点与另一个点的线段为斜边,构造出直角三角形,再运用勾股定理求最短路径.
小试牛刀
1.从电线杆上离地面5m的C处向地面拉一条长为7m的钢缆,则地面钢缆A到电线杆底部B的距离是 ( )
A.24m B.12m C. m D. m
D
小试牛刀
2.如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是 ( )
A.9cm B.12cm C.15cm D.18cm
D
3.已知点(2,5),(-4,-3),则这两点的距离为_______.
10
小试牛刀
4、已知如图所示,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20 m,你能求出A,B两点间的距离吗(结果保留整数)?
在RtΔABC中,根据勾股定理:
AB2=BC2-AC2=602-202 = 3200
所以,AC= ≈ 57
A,B两点间的距离约为57
5. 为筹备迎接新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图.已知圆筒的高为108cm,其横截面周长为36cm,如果在表面均匀缠绕油纸4圈,应裁剪多长的油纸?
小试牛刀
课堂小结
1.利用勾股定理解决实际问题的一般步骤是什么?
2.两点之间的距离公式及在求距离时需要注意什么?
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
第十七章
17.1勾股定理
第二课时
勾股定理在实际生活中的应用
人教版数学 八年级下册
学习目标
能运用勾股定理及直角三角形的判定条件解决实际问题.
能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
问题 观看下面同一根长竹竿以三种不同的方式进门的情况,对于长竹竿进门之类的问题你有什么启发?
这个跟我们学的勾股定理有关,将实际问题转化为数学问题
新课引入
新知讲解
例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过 为什么
2m
1m
A
B
D
C
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
分析:可以看出木板横着,竖着都不能通过,只能斜着.门框AC的长度是斜着能通过的最大长度,只要AC的长大于木板的宽就能通过.
新知讲解
A
B
D
C
O
解:在Rt△ABC中,根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1,
∴OB=1.
在Rt△COD中,根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
例2 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m. 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
新知讲解
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
数学问题
直角三角形
勾股定理
实际问题
转化
建 构
利用
解 决
新知讲解
想一想:在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A ′ B ′ C ′ 中,∠C=∠C ′=90°,AB=A′ B ′,AC=A′ C′ .
求证:△ABC≌△A ′B ′C′ .
A
B
C
A
B
C′
′
′
新知讲解
证明:在Rt△ABC 和Rt△A ′B ′C ′中,∠C=∠C′=90°,
根据勾股定理得
A
B
C
A
B
C′
′
′
A
2
1
-4
-3
-2
-1
-1
2
3
1
4
5
例3 如图,在平面直角坐标系中有两点A(-3,5),B(1,2)求A,B两点间的距离.
y
O
x
3
B
C
解:如图,过点A作x轴的垂线,过点B作x,y轴的垂线.相交于点C,连接AB.
∴AC=5-2=3,BC=3+1=4,
在Rt△ABC中,由勾股定理得
∴ A,B两点间的距离为5.
新知讲解
新知讲解
方法总结:
两点之间的距离公式:
一般地,设平面上任意两点
C
B
A
问题 在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B 路线,难道小狗也懂数学?
AC+CB >AB(两点之间线段最短)
思考:在立体图形中,怎么寻找最短线路呢?
新知讲解
A
B
A'
A
B
B
A
O
想一想:蚂蚁走哪一条路线最近?
蚂蚁A→B的路线
问题:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想沿侧面从A处爬向B处,蚂蚁怎么走最近?
B
A
根据两点之间线段最短易知第三个路线最近.
新知讲解
若已知圆柱体高为12 cm,底面半径为3 cm,π取3.
B
A
3
O
12
侧面展开图
12
3π
A
B
A'
A'
解:在Rt△ABA′中,由勾股定理得
新知讲解
立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
新知讲解
例4 有一个圆柱形油罐,要以A点环绕油罐建梯子,正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2 m,高AB是5 m,π取3)
A
B
A
B
A'
B'
解:油罐的展开图如图,则AB'为梯子的最短距离.
∵AA'=2×3×2=12, A'B'=5,
∴AB'=13. 即梯子最短需13米.
新知讲解
数学思想:
立体图形
平面图形
转化
展开
新知讲解
B
牛奶盒
A
【变式题】看到小蚂蚁终于喝到饮料的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程么?
6cm
8cm
10cm
例5 如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?
牧童A
小屋B
A′
C
东
北
解:如图,作出点A关于河岸的对称点A′,连接A′B则A′B就是最短路线.
由题意得A′C=4+4+7=15(km),BC=8km.
在Rt△A′CB中,由勾股定理得
新知讲解
新知讲解
求直线同侧的两点到直线上一点所连线段的和的最短路径的方法:先找到其中一点关于这条直线的对称点,连接对称点与另一点的线段就是最短路径长,以连接对称点与另一个点的线段为斜边,构造出直角三角形,再运用勾股定理求最短路径.
小试牛刀
1.从电线杆上离地面5m的C处向地面拉一条长为7m的钢缆,则地面钢缆A到电线杆底部B的距离是 ( )
A.24m B.12m C. m D. m
D
小试牛刀
2.如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是 ( )
A.9cm B.12cm C.15cm D.18cm
D
3.已知点(2,5),(-4,-3),则这两点的距离为_______.
10
小试牛刀
4、已知如图所示,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20 m,你能求出A,B两点间的距离吗(结果保留整数)?
在RtΔABC中,根据勾股定理:
AB2=BC2-AC2=602-202 = 3200
所以,AC= ≈ 57
A,B两点间的距离约为57
5. 为筹备迎接新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图.已知圆筒的高为108cm,其横截面周长为36cm,如果在表面均匀缠绕油纸4圈,应裁剪多长的油纸?
小试牛刀
课堂小结
1.利用勾股定理解决实际问题的一般步骤是什么?
2.两点之间的距离公式及在求距离时需要注意什么?
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
