人教版八年级数学下册17.2第2课时勾股定理逆定理的应用 课件(共26张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.2第2课时勾股定理逆定理的应用 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 08:54:52 | ||
图片预览






文档简介
(共26张PPT)
第十七章
17.2勾股定理逆定理
第二课时
勾股定理的逆定理的应用
人教版数学 八年级下册
学习目标
灵活应用勾股定理及其逆定理解决实际问题.
进一步加深性质定理与判定定理之间关系的认识.
将实际问题转化成用勾股定理的逆定理解决的数学问题.
在军事和航海上经常要确定方向和位置,从而常需要使用一些数学知识和方法,其中勾股定理的逆定理经常会被用到,这节课让我们一起来学习吧.
新知讲解
勾股定理的逆定理的内容和作用是什么?
新知讲解
如果三角形的三边长a、b、c满足
a2 + b2 = c2
那么这个三角形是直角三角形。
判定直角三角形
作用:
逆定理:
1
2
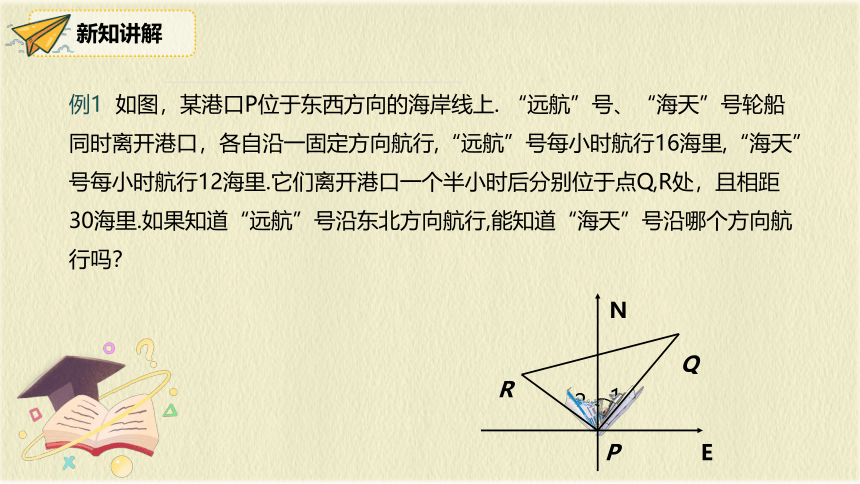
例1 如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
N
E
P
Q
R
新知讲解
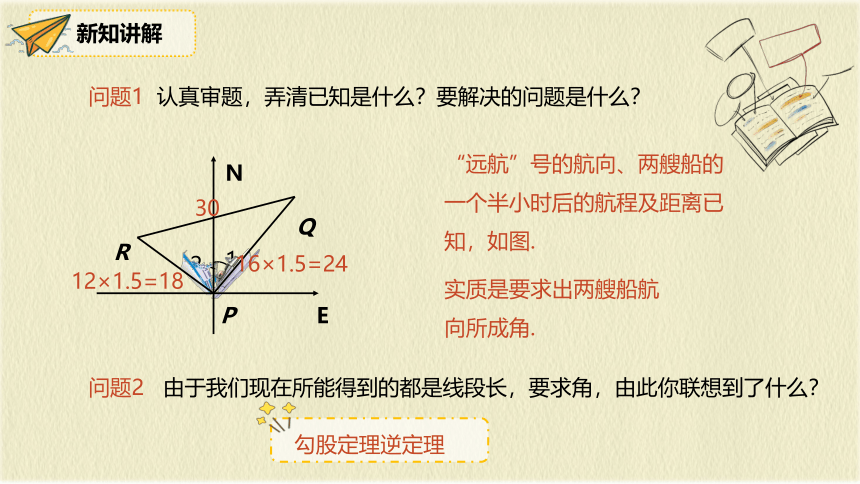
问题1 认真审题,弄清已知是什么?要解决的问题是什么?
1
2
N
E
P
Q
R
16×1.5=24
12×1.5=18
30
“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如图.
问题2 由于我们现在所能得到的都是线段长,要求角,由此你联想到了什么?
实质是要求出两艘船航
向所成角.
勾股定理逆定理
新知讲解
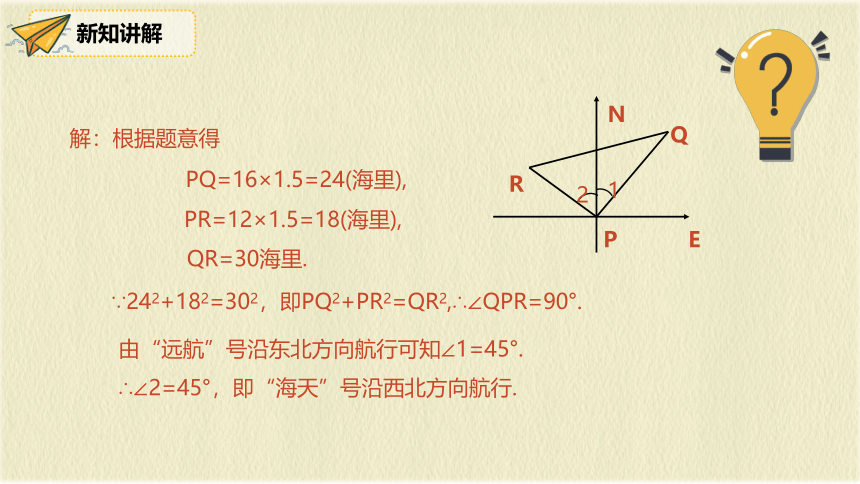
解:根据题意得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30海里.
∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
新知讲解
新知讲解
解决实际问题的步骤:
1.构建几何模型(从整体到局部);
2.标注有用信息,明确已知和所求;
3.应用数学知识求解.
【变式题】 如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
东
北
P
A
B
C
Q
D
分析:根据勾股定理的逆定可得△ABC是直角三角形,然后利用勾股定理的逆定理及直角三角形的面积公式可求PD,然后再利用勾股定理便可求CD.
新知讲解
解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三
角形面积公式有 BC·AB= AC·BD,
即6×8=10BD,解得BD=
在Rt△BCD中,
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
东
北
P
A
B
C
Q
D
新知讲解
例2 一个零件的形状如图 所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图 所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图
图
新知讲解
在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.
D
A
B
C
4
3
5
13
12
图
新知讲解
1.A、B、C三地的两两距离如图所示,A地在B地的正东方向,C在B地的什么方向?
A
B
C
5cm
12cm
13cm
解:∵ BC2+AB2=52+122=169,
AC2 =132=169,
∴BC2+AB2=AC2,
即△ABC是直角三角形,
∠B=90°.
答:C在B地的正北方向.
新知讲解
2.如图是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:∵AB=DC=8m,AD=BC=6m,
∴AB2+BC2=82+62=64+36=100.
又∵AC2=92=81,
∴AB2+BC2≠AC2,
∴∠ABC≠90°,
∴该农民挖的不合格.
新知讲解
例3 如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
解析:连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
A
D
B
C
3
4
13
12
新知讲解
解:连接AC.
A
D
B
C
3
4
13
12
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
新知讲解
新知讲解
四边形问题对角线是常用的辅助线,它把四边形问题转化成两个三角形的问题.在使用勾股定理的逆定理解决问题时,它与勾股定理是“黄金搭挡”,经常配套使用.
【变式题1】 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:连接BD.
在Rt△ABD中,
由勾股定理得 BD2=AB2+AD2,
∴BD=5m.
又∵ CD=12cm,BC=13cm,
∴ BC2=CD2+BD2,∴△BDC是直角三角形.
∴S四边形ABCD=SRt△BCD-SRt△ABD= BD CD- AB AD
= ×(5×12-3×4)=24 (cm2).
C
B
A
D
新知讲解
【变式题2】 如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积.
解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm.
又∵
∴△ABC是直角三角形, ∠B是直角.
∴
D
C
B
A
新知讲解
(1)证明:∵CD=1,BC= 5 ,BD=2,
∴CD2+BD2=BC2,
∴△BDC是直角三角形;
(2)解:设腰长AB=AC=x,
在Rt△ADB中,∵AB2=AD2+BD2,
∴x2=(x-1)2+22,
解得
用到了方程的思想
例4 如图,△ABC中,AB=AC,D是AC边上的一点,CD=1,BC= 5 ,BD=2.
(1)求证:△BCD是直角三角形;
(2)求△ABC的面积.
新知讲解
1. 医院、公园和超市的平面示意图如图所示,超市在医院的南偏东25°的方向,且到医院的距离为300m,公园到医院的距离为400m.若公园到超市的距离为500m,则公园在医院的北偏东 的方向.
东
医院
公园
超市
北
65°
小试牛刀
2.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中摆放方法正确的是 ( )
A. B.
C. D.
D
小试牛刀
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行了12×2=24(km),B组行了9×2=18(km),
又∵A,B两组相距30km,
且有242+182=302,
∴A,B两组行进的方向成直角.
小试牛刀
4.如图,在△ABC中,AB=17,BC=16,BC边上的中线AD=15,试说明:AB=AC.
解:∵BC=16,AD是BC边上的中线,
∴BD=CD= BC=8.
∵在△ABD中,
AD2+BD2=152+82=172=AB2,
∴△ABD是直角三角形,即∠ADB=90°.
∴△ADC是直角三角形.
在Rt△ADC中,
∴AB=AC.
小试牛刀
课堂小结
1.勾股定理的逆定理的内容和作用是什么?
2.用勾股定理的逆定理解决实际问题的步骤有哪些?
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
第十七章
17.2勾股定理逆定理
第二课时
勾股定理的逆定理的应用
人教版数学 八年级下册
学习目标
灵活应用勾股定理及其逆定理解决实际问题.
进一步加深性质定理与判定定理之间关系的认识.
将实际问题转化成用勾股定理的逆定理解决的数学问题.
在军事和航海上经常要确定方向和位置,从而常需要使用一些数学知识和方法,其中勾股定理的逆定理经常会被用到,这节课让我们一起来学习吧.
新知讲解
勾股定理的逆定理的内容和作用是什么?
新知讲解
如果三角形的三边长a、b、c满足
a2 + b2 = c2
那么这个三角形是直角三角形。
判定直角三角形
作用:
逆定理:
1
2
例1 如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
N
E
P
Q
R
新知讲解
问题1 认真审题,弄清已知是什么?要解决的问题是什么?
1
2
N
E
P
Q
R
16×1.5=24
12×1.5=18
30
“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如图.
问题2 由于我们现在所能得到的都是线段长,要求角,由此你联想到了什么?
实质是要求出两艘船航
向所成角.
勾股定理逆定理
新知讲解
解:根据题意得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30海里.
∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
新知讲解
新知讲解
解决实际问题的步骤:
1.构建几何模型(从整体到局部);
2.标注有用信息,明确已知和所求;
3.应用数学知识求解.
【变式题】 如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
东
北
P
A
B
C
Q
D
分析:根据勾股定理的逆定可得△ABC是直角三角形,然后利用勾股定理的逆定理及直角三角形的面积公式可求PD,然后再利用勾股定理便可求CD.
新知讲解
解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三
角形面积公式有 BC·AB= AC·BD,
即6×8=10BD,解得BD=
在Rt△BCD中,
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
东
北
P
A
B
C
Q
D
新知讲解
例2 一个零件的形状如图 所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图 所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图
图
新知讲解
在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.
D
A
B
C
4
3
5
13
12
图
新知讲解
1.A、B、C三地的两两距离如图所示,A地在B地的正东方向,C在B地的什么方向?
A
B
C
5cm
12cm
13cm
解:∵ BC2+AB2=52+122=169,
AC2 =132=169,
∴BC2+AB2=AC2,
即△ABC是直角三角形,
∠B=90°.
答:C在B地的正北方向.
新知讲解
2.如图是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:∵AB=DC=8m,AD=BC=6m,
∴AB2+BC2=82+62=64+36=100.
又∵AC2=92=81,
∴AB2+BC2≠AC2,
∴∠ABC≠90°,
∴该农民挖的不合格.
新知讲解
例3 如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
解析:连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
A
D
B
C
3
4
13
12
新知讲解
解:连接AC.
A
D
B
C
3
4
13
12
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
新知讲解
新知讲解
四边形问题对角线是常用的辅助线,它把四边形问题转化成两个三角形的问题.在使用勾股定理的逆定理解决问题时,它与勾股定理是“黄金搭挡”,经常配套使用.
【变式题1】 如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:连接BD.
在Rt△ABD中,
由勾股定理得 BD2=AB2+AD2,
∴BD=5m.
又∵ CD=12cm,BC=13cm,
∴ BC2=CD2+BD2,∴△BDC是直角三角形.
∴S四边形ABCD=SRt△BCD-SRt△ABD= BD CD- AB AD
= ×(5×12-3×4)=24 (cm2).
C
B
A
D
新知讲解
【变式题2】 如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积.
解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm.
又∵
∴△ABC是直角三角形, ∠B是直角.
∴
D
C
B
A
新知讲解
(1)证明:∵CD=1,BC= 5 ,BD=2,
∴CD2+BD2=BC2,
∴△BDC是直角三角形;
(2)解:设腰长AB=AC=x,
在Rt△ADB中,∵AB2=AD2+BD2,
∴x2=(x-1)2+22,
解得
用到了方程的思想
例4 如图,△ABC中,AB=AC,D是AC边上的一点,CD=1,BC= 5 ,BD=2.
(1)求证:△BCD是直角三角形;
(2)求△ABC的面积.
新知讲解
1. 医院、公园和超市的平面示意图如图所示,超市在医院的南偏东25°的方向,且到医院的距离为300m,公园到医院的距离为400m.若公园到超市的距离为500m,则公园在医院的北偏东 的方向.
东
医院
公园
超市
北
65°
小试牛刀
2.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中摆放方法正确的是 ( )
A. B.
C. D.
D
小试牛刀
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行了12×2=24(km),B组行了9×2=18(km),
又∵A,B两组相距30km,
且有242+182=302,
∴A,B两组行进的方向成直角.
小试牛刀
4.如图,在△ABC中,AB=17,BC=16,BC边上的中线AD=15,试说明:AB=AC.
解:∵BC=16,AD是BC边上的中线,
∴BD=CD= BC=8.
∵在△ABD中,
AD2+BD2=152+82=172=AB2,
∴△ABD是直角三角形,即∠ADB=90°.
∴△ADC是直角三角形.
在Rt△ADC中,
∴AB=AC.
小试牛刀
课堂小结
1.勾股定理的逆定理的内容和作用是什么?
2.用勾股定理的逆定理解决实际问题的步骤有哪些?
谢谢观看!
注:本课件所有素材来源于网络,如有侵权,请联系我们。
