人教版数学五年级下册9.2《图形和几何》课件(共22张PPT)
文档属性
| 名称 | 人教版数学五年级下册9.2《图形和几何》课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 29.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 09:45:14 | ||
图片预览




文档简介
(共22张PPT)
图形与几何
人教版 五年级下册
学习目标
激发对学习空间和图形的兴趣,积极参加教学活动,主动和他人合作交流的意识。
能感悟图形的形状,进一步丰富学生对几何图形的认识。
学会观察物体和图形的运动,认识长方体和正方体的计算,会灵活应用。
观察物体、图形的运动
观察物体
根据从正面、左面和上面看到的图形摆几何体。
图形的运动
图形旋转的性质和特征
用图形变换还原基本图形
旋转的意义和三要素
新课讲解
【观察物体】
根据从正面、左面或上面看到的图形摆几何体:根据从一个方向看到的图形摆几何体,使小正方体的行数、列数、层数符合要求,所摆的几何体通常不止一种。
根据从正面、左面或上面看到的图形摆几何体:先根据从上面看到的图形确定小正方体的列数和行数,再根据从正面和左面看到的图形确定各列和各行小正方体的层数,所摆的几何体通常只有一种。
新课讲解
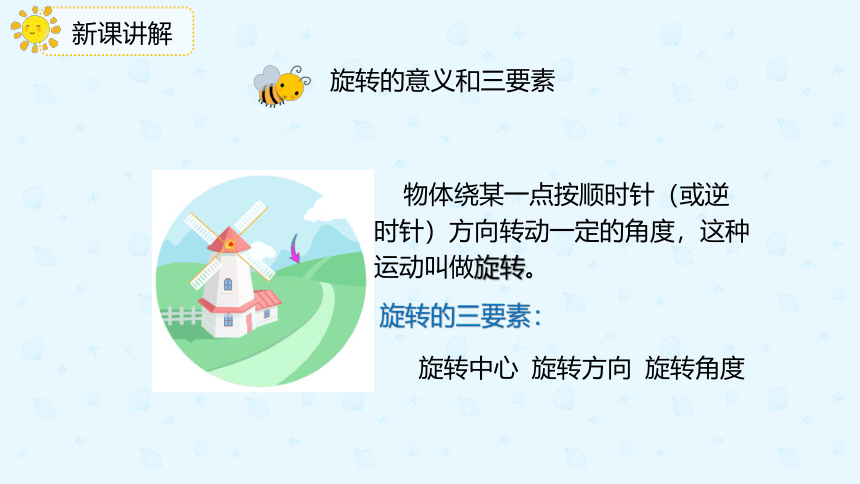
物体绕某一点按顺时针(或逆时针)方向转动一定的角度,这种运动叫做旋转。
旋转的三要素:
旋转中心
旋转方向
旋转角度
旋转的意义和三要素
新课讲解
图形旋转,图形中所有点和线段都旋转相应的
度数,对应点到旋转点的距离相等,对应线段相等,
对应角相等。图形旋转后,形状、大小都没有变化,
只有位置和方向变了。
图形旋转的性质和特征
新课讲解
长方体和正方体
长方体与正方体的认识
表面积的意义
长方体和正方体的表面积
体积的意义与单位
体积的计算方法
长方体和正方体的体积
表面积的计算方法
新课讲解
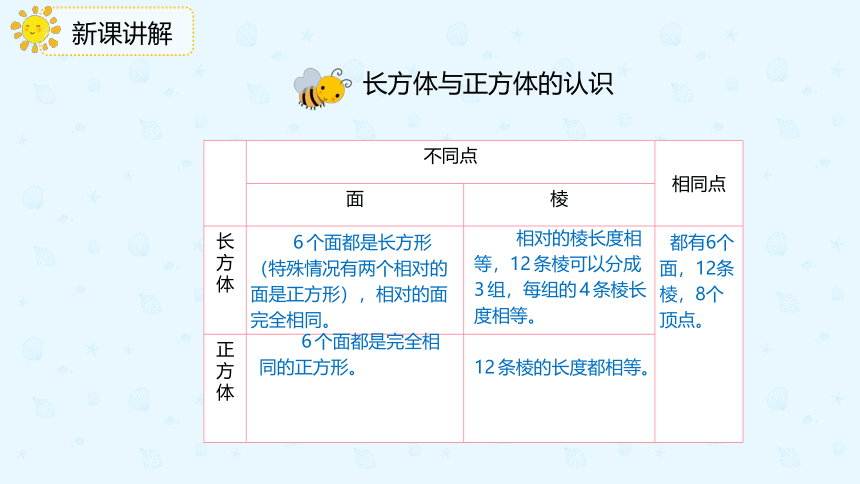
不同点 相同点
面 棱
长方体
正方体
6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面完全相同。
6个面都是完全相同的正方形。
相对的棱长度相等,12条棱可以分成3组,每组的4条棱长度相等。
12条棱的长度都相等。
都有6个面,12条棱,8个顶点。
长方体与正方体的认识
新课讲解
新课讲解
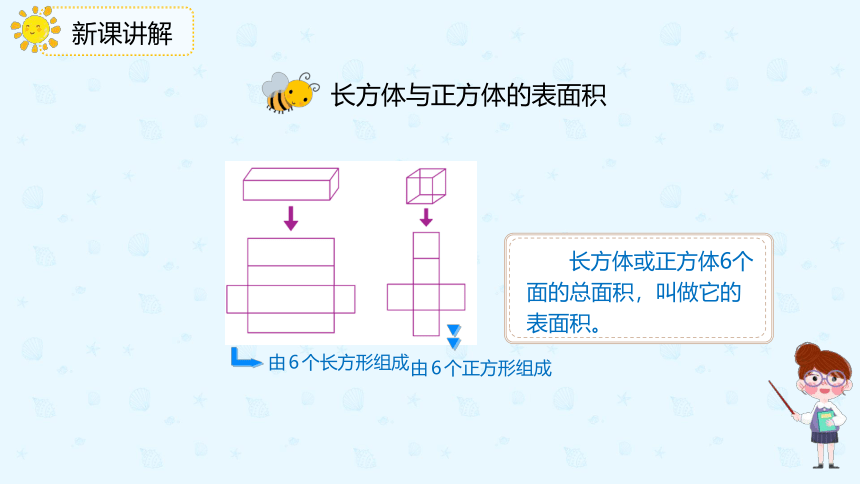
长方体与正方体的表面积
由6个长方形组成
由6个正方形组成
长方体或正方体6个面的总面积,叫做它的表面积。
新课讲解
长方体与正方体表面积的计算方法:
长方体的表面积:(长×宽+长×高+宽×高)×2
正方体的表面积:棱长×棱长×6
新课讲解
物体所占空间的大小叫做物体的体积。
体积和体积单位
单位名称 相邻两个单位间的进率
长度 米,分米,厘米
面积 平方米,平方分米,平方厘米
体积 立方米,立方分米,立方厘米
10
100
1000
新课讲解
长方体与正方体体积的计算方法:
长方体的体积:长×宽×高
正方体的体积:棱长×棱长×棱长
V=abh
V=a
正方体或长方体的体积:底面积×高
V=Sh
新课讲解
箱子、油桶、仓库等所能容纳物体的体积,通常叫做容器的容积。
1L=1000mL 1L=1dm 1mL=1cm
计量容积,一般就用体积单位。计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写成L和mL。
容积和体积单位
新课讲解
长方体或正方体容器容积的计算方法,跟体积的计算方法相同,但要从容器里面量长、宽、高。
不规则物体容积的计算方法,一是将不规则物体转化成规则物体;二是用排水测量法测量物体体积。
有些物体放入水中,会浮在水面或溶解、融化,则这类物品不能用排水测量法测量物体的体积,如乒乓球、冰块的体积等。
容积的计算方法
课堂练习
1.一个长方体游泳池,长30m,宽10m,深1.6m,池的四壁和底边都铺砌瓷砖。如果每平方米用瓷砖25块,共需要瓷砖多少块?
30×10+30×1.6×2+10×1.6×2=428(m )
25×428=10700(块)
答:共需要瓷砖10700块。
课堂练习
2.分别求出下面长方体、正方体的表面积和体积(单位:cm)
7.5×4×4+42×2=152(cm2)
4×4×7.5=120(cm3)
1.52×6=13.5(cm2)
1.53=3.375(cm3)
课堂练习
3.一个体积为160cm 的长方体中相邻两个面的面积分别为20cm 和32cm ,求它的表面积。
160÷20=8(cm)
160÷32=5(cm)
(8×5+20+32)×2=184(cm )
答:它的表面积是184平方厘米。
课堂练习
4.画一画。
(1)将图形A像右平移5格,得到图形B。
(2)将图形A绕点O顺时针旋转90°,得到图形C。
O1
B
C
5.在一个长5m、宽2m的水池中,放入一块棱长为10dm的正方体石块,这时水深为20dm。如果把这个石块从水池中拿出来,水池中的水深变为多少?
10dm=1m
20dm=2m
(5×2×2 1×1×1)÷(5×2)=1.9(m)
答:水池中的水深变为1.9米。
课堂小结
课堂小结
1.观察物体
2.旋转
3.长方体和正方体
1、课后练习P56第1、2题;
2、练习册P45.
课后作业
感 谢 聆 听
人教版 五年级下册
注:本课件所有素材来源于网络,如有侵权,请联系我们。
图形与几何
人教版 五年级下册
学习目标
激发对学习空间和图形的兴趣,积极参加教学活动,主动和他人合作交流的意识。
能感悟图形的形状,进一步丰富学生对几何图形的认识。
学会观察物体和图形的运动,认识长方体和正方体的计算,会灵活应用。
观察物体、图形的运动
观察物体
根据从正面、左面和上面看到的图形摆几何体。
图形的运动
图形旋转的性质和特征
用图形变换还原基本图形
旋转的意义和三要素
新课讲解
【观察物体】
根据从正面、左面或上面看到的图形摆几何体:根据从一个方向看到的图形摆几何体,使小正方体的行数、列数、层数符合要求,所摆的几何体通常不止一种。
根据从正面、左面或上面看到的图形摆几何体:先根据从上面看到的图形确定小正方体的列数和行数,再根据从正面和左面看到的图形确定各列和各行小正方体的层数,所摆的几何体通常只有一种。
新课讲解
物体绕某一点按顺时针(或逆时针)方向转动一定的角度,这种运动叫做旋转。
旋转的三要素:
旋转中心
旋转方向
旋转角度
旋转的意义和三要素
新课讲解
图形旋转,图形中所有点和线段都旋转相应的
度数,对应点到旋转点的距离相等,对应线段相等,
对应角相等。图形旋转后,形状、大小都没有变化,
只有位置和方向变了。
图形旋转的性质和特征
新课讲解
长方体和正方体
长方体与正方体的认识
表面积的意义
长方体和正方体的表面积
体积的意义与单位
体积的计算方法
长方体和正方体的体积
表面积的计算方法
新课讲解
不同点 相同点
面 棱
长方体
正方体
6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面完全相同。
6个面都是完全相同的正方形。
相对的棱长度相等,12条棱可以分成3组,每组的4条棱长度相等。
12条棱的长度都相等。
都有6个面,12条棱,8个顶点。
长方体与正方体的认识
新课讲解
新课讲解
长方体与正方体的表面积
由6个长方形组成
由6个正方形组成
长方体或正方体6个面的总面积,叫做它的表面积。
新课讲解
长方体与正方体表面积的计算方法:
长方体的表面积:(长×宽+长×高+宽×高)×2
正方体的表面积:棱长×棱长×6
新课讲解
物体所占空间的大小叫做物体的体积。
体积和体积单位
单位名称 相邻两个单位间的进率
长度 米,分米,厘米
面积 平方米,平方分米,平方厘米
体积 立方米,立方分米,立方厘米
10
100
1000
新课讲解
长方体与正方体体积的计算方法:
长方体的体积:长×宽×高
正方体的体积:棱长×棱长×棱长
V=abh
V=a
正方体或长方体的体积:底面积×高
V=Sh
新课讲解
箱子、油桶、仓库等所能容纳物体的体积,通常叫做容器的容积。
1L=1000mL 1L=1dm 1mL=1cm
计量容积,一般就用体积单位。计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写成L和mL。
容积和体积单位
新课讲解
长方体或正方体容器容积的计算方法,跟体积的计算方法相同,但要从容器里面量长、宽、高。
不规则物体容积的计算方法,一是将不规则物体转化成规则物体;二是用排水测量法测量物体体积。
有些物体放入水中,会浮在水面或溶解、融化,则这类物品不能用排水测量法测量物体的体积,如乒乓球、冰块的体积等。
容积的计算方法
课堂练习
1.一个长方体游泳池,长30m,宽10m,深1.6m,池的四壁和底边都铺砌瓷砖。如果每平方米用瓷砖25块,共需要瓷砖多少块?
30×10+30×1.6×2+10×1.6×2=428(m )
25×428=10700(块)
答:共需要瓷砖10700块。
课堂练习
2.分别求出下面长方体、正方体的表面积和体积(单位:cm)
7.5×4×4+42×2=152(cm2)
4×4×7.5=120(cm3)
1.52×6=13.5(cm2)
1.53=3.375(cm3)
课堂练习
3.一个体积为160cm 的长方体中相邻两个面的面积分别为20cm 和32cm ,求它的表面积。
160÷20=8(cm)
160÷32=5(cm)
(8×5+20+32)×2=184(cm )
答:它的表面积是184平方厘米。
课堂练习
4.画一画。
(1)将图形A像右平移5格,得到图形B。
(2)将图形A绕点O顺时针旋转90°,得到图形C。
O1
B
C
5.在一个长5m、宽2m的水池中,放入一块棱长为10dm的正方体石块,这时水深为20dm。如果把这个石块从水池中拿出来,水池中的水深变为多少?
10dm=1m
20dm=2m
(5×2×2 1×1×1)÷(5×2)=1.9(m)
答:水池中的水深变为1.9米。
课堂小结
课堂小结
1.观察物体
2.旋转
3.长方体和正方体
1、课后练习P56第1、2题;
2、练习册P45.
课后作业
感 谢 聆 听
人教版 五年级下册
注:本课件所有素材来源于网络,如有侵权,请联系我们。
