浙江省乐清市第二中学2013届高三第一次月考数学(文)试题
文档属性
| 名称 | 浙江省乐清市第二中学2013届高三第一次月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 518.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
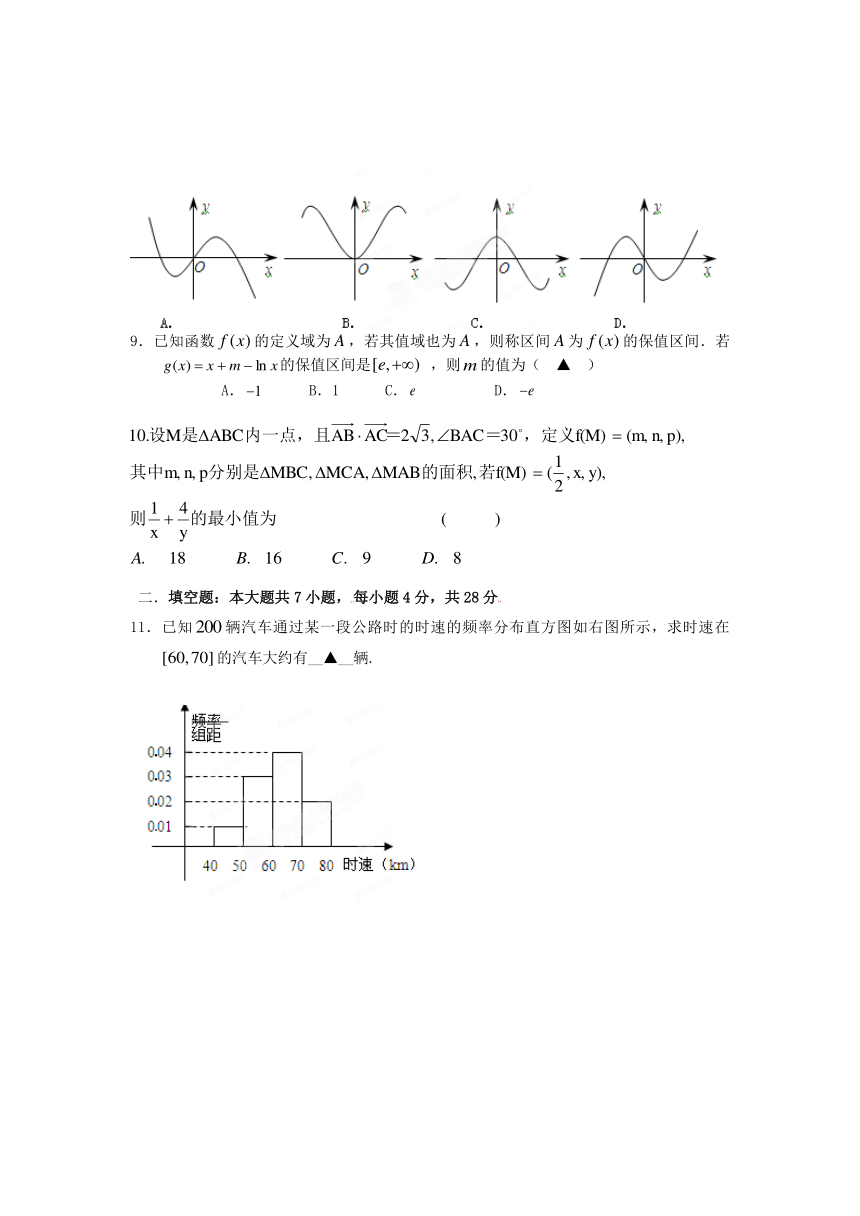
| 科目 | 数学 | ||
| 更新时间 | 2012-11-13 00:00:00 | ||
图片预览

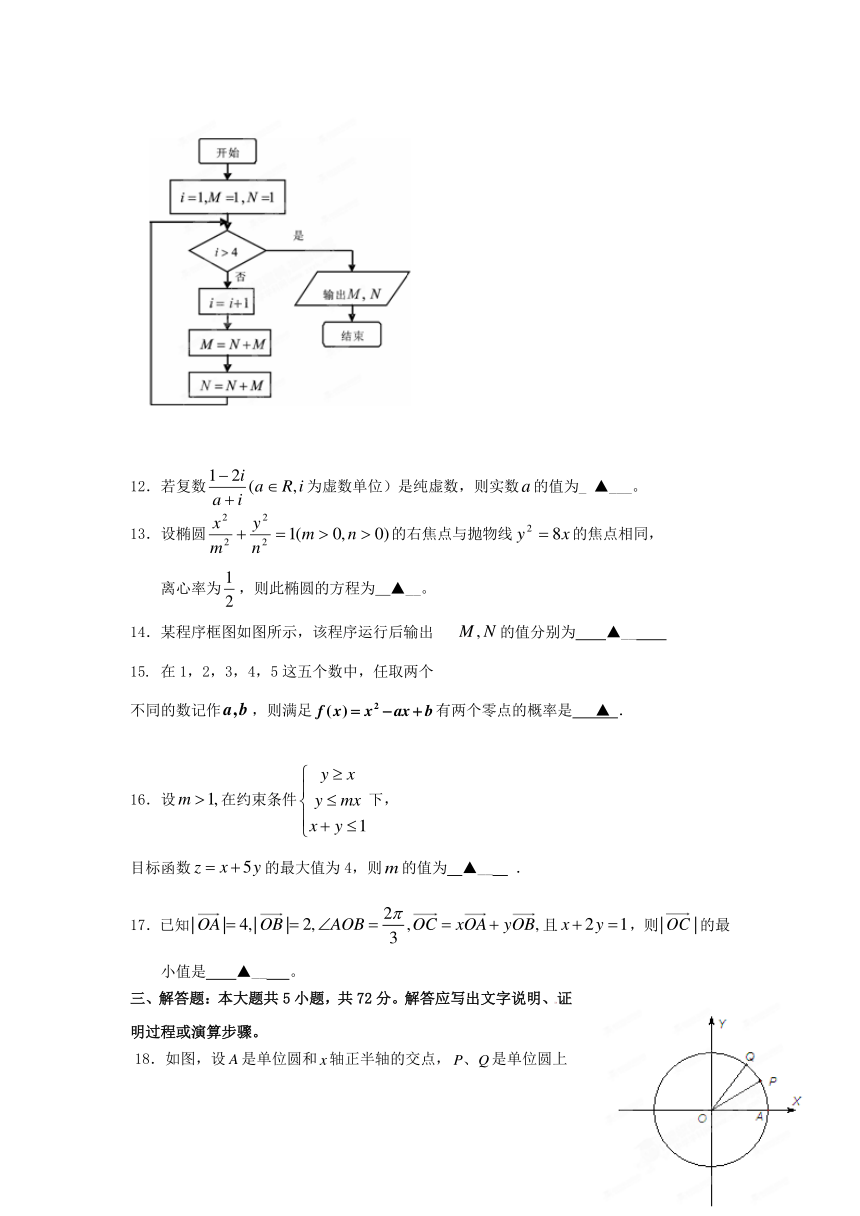

文档简介
(时间:120分钟, 满分:150分,本次考试不得使用计算器)
一.选择题:本大题共10题,每小题5分,共50分.
1.若集合,则为( ▲ )
A. B. C. D.
2.已知是平面,是直线,则下列命题中不正确的是( ▲ ).
A.若,,则 B.若,,则
C.若,,则 D.若,,则
3.设等比数列的前n项和为,已知,
则的值是 ( ▲ )
A. B. C. D.
4.一空间几何体三视图如图所示,
则该几何体的体积为 ( ▲ )
A. B. C.2 D.6
5.函数是( ▲ ).
A.周期为的奇函数 B.周期为的偶函数
C.周期为的奇函数 D.周期为的偶函数
6.“a>0”是“方程至少有一个负数根”的 ( ▲ )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
7.下列命题中是假命题的是 ( ▲ )
A.,使是幂函数,且在上递减
B.,函数有零点
C.,使
D.,函数都不是偶函数
8.设曲线在点处的切线的斜率为,则函数的部分图象可以为
( ▲ )
9.已知函数的定义域为,若其值域也为,则称区间为的保值区间.若的保值区间是 ,则的值为( ▲ )
A. B.1 C. D.
二.填空题:本大题共7小题,每小题4分,共28分
11.已知辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,求时速在的汽车大约有__▲__辆.
12.若复数为虚数单位)是纯虚数,则实数的值为_ ▲___。
13.设椭圆的右焦点与抛物线的焦点相同,
离心率为,则此椭圆的方程为_▲__。
14.某程序框图如图所示,该程序运行后输出 的值分别为? ▲__?
15. 在1,2,3,4,5这五个数中,任取两个
不同的数记作,则满足有两个零点的概率是 ▲ .
16.设在约束条件下,
目标函数的最大值为4,则的值为 ▲__ .
17.已知且,则的最小值是 ▲__ 。
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.如图,设是单位圆和轴正半轴的交点,是单位圆上
的两点,是坐标原点,,.
(1)若,求的值;
(2)设函数,求的值域.
19.(本题满分14分)如图,已知平面,∥,
是正三角形,且.
(1)设是线段的中点,求证:∥平面;
(2)求直线与平面所成角的余弦值.
20.(本小题14分)已知数列的前项和为,且,数列为等差数列,且公差,。
(1)求数列的通项公式;
(2)若成等比数列,求数列的前项和。
.co
m21.(本小题满分15分)已知.
(I)如果函数的单调递减区间为,求函数的解析式;
(II)在(Ⅰ)的条件下,求函数y=的图像在点处的切线方程;
(III)若不等式恒成立,求实数的取值范围.
22、(本题满分15分)已知抛物线:(),焦点为,直线交抛物线于、两点,是线段的中点,
过作轴的垂线交抛物线于点,
(1)若抛物线上有一点到焦点的距离为,求此时的值;
(2)是否存在实数,使是以为直角顶点的直角三角形?若存在,求出的值;若不存在,说明理由。
一.选择题 : 本大题共10小题, 每小题5分, 共50分.
11、80 12、 2 13、 14、 34 55
15、 16、 3 17、
三、解答题:(本大题共5小题,共52分. 解答应写出文字说明、证明过程或演算步骤)
………………………………11分
……………………………12分
………………………………14分
19、解: (I)证明:取CE中点N,连接MN,BN
则MN∥DE∥AB且MN=DE=AB
∴四边形ABNM为平行四边形∴AM∥BN ………....4分
∴AM∥平面BCE ………………………....6分
(Ⅱ)解:取AD中点H,连接BH,
∵是正三角形, ∴CH⊥AD …....8分
又∵平面 ∴CH⊥AB
∴CH⊥平面ABED ....10分
∴∠CBH为直线 与平面所成的角………....12分
设AB=a,则AC=AD=2a , ∴BH=a BC=a
cos∠CBH= ………………....14分
(2)∵,∴…………(8分)
由题意,而
设,∴,∴,得或(舍去)…………(13分)
故……………(14分)
21.解:(1) 由题意的解集是
即的两根分别是.
将或代入方程得.
. …………4分
(2)由(Ⅰ)知:,,
点处的切线斜率,
函数y=的图像在点处的切线方程为:
,即. …………9分
的取值范围是. …………15分
22、(本题满分15分)已知抛物线:(),焦点为,直线交抛物线于、两点,是线段的中点,过作轴的垂线交抛物线于点,
解:(1)抛物线的焦点,---------------------------------------------------2分
,得。----------------------------------6分
(或利用得
,或(舍去))
,-------------------------------------------------------------10分
得,
若存在实数,使是以为直角顶点的直角三角形,则,-----11分
即,结合()化简得,
同课章节目录
