3.2 函数模型及其应用(Word含答案解析)
文档属性
| 名称 | 3.2 函数模型及其应用(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 194.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 13:13:50 | ||
图片预览


文档简介
3.2 函数模型及其应用
一、选择题(共10小题;共50分)
1. 某种商品进价为每件 元,按进价增加 出售,后因库存积压降价,按九折出售,每件还获利
A. 元 B. 元 C. 元 D. 元
2. 三个变量 随着变量 的变化情况如下表:
则与 呈对数型函数、指数型函数、幂函数型函数变化的变量依次是
A. B. C. D.
3. 某产品的总成本 (万元)与产量 (台)之间的函数关系是 ,若每件产品的售价为 万元,则生产者不亏本时(销售收入不小于总成本)的最低产量为
A. 台 B. 台 C. 台 D. 台
4. 某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过 立方米的,按每立方米 元水费收费;用水超过 立方米的,超过部分按每立方米 元收费.某职工某月缴水费 元,则该职工这个月实际用水为
A. 立方米 B. 立方米 C. 立方米 D. 立方米
5. 据报道,青海的湖水量在最近 年内减少了 ,如果按此规律,设 2010 年的湖水量为 ,从 2010 年起,过 年后湖水量 与 的函数关系式为
A. B.
C. D.
6. 已知每生产100克饼干的原材料加工费为1.8元.某食品加工厂对饼干采用两种包装,其包装费用、销售价格如下表所示:
则下列说法中正确的是
①买小包装实惠 ②买大包装实惠 ③卖 小包比卖 大包盈利多 ④卖 大包比卖 小包盈利多
A. ①③ B. ①④ C. ②③ D. ②④
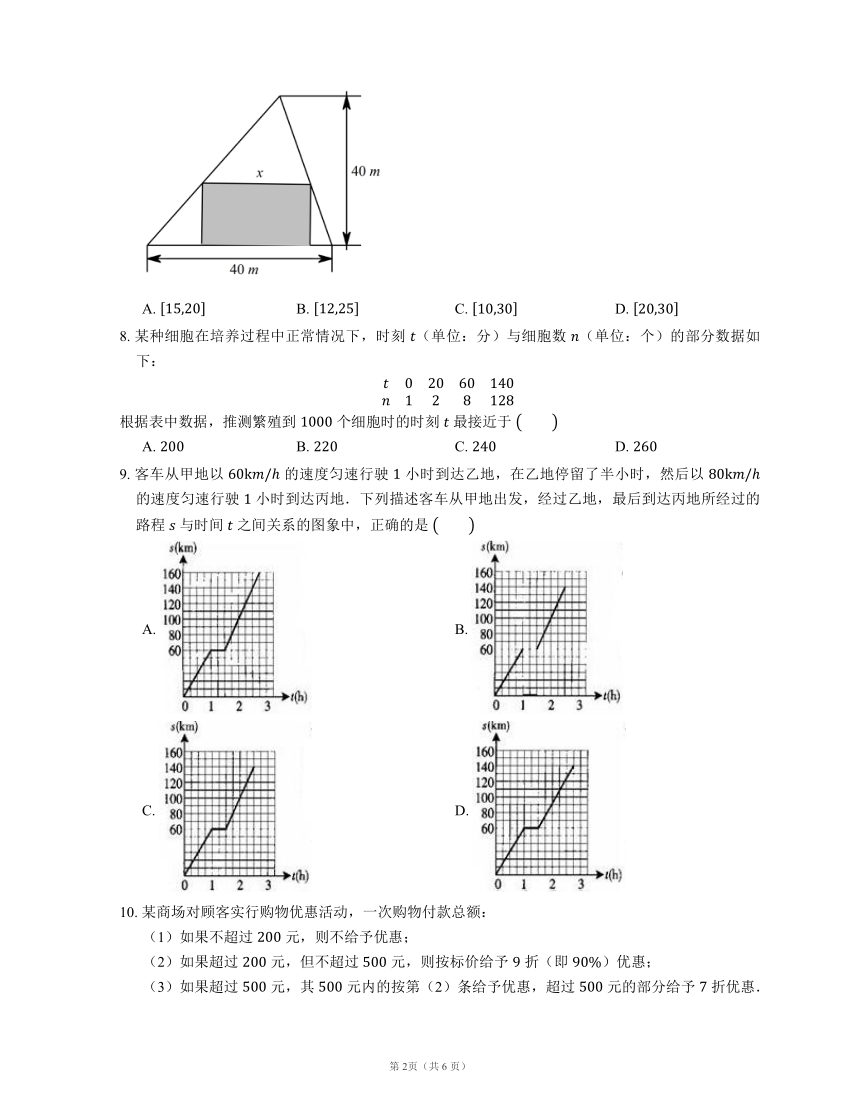
7. 在如图所示的锐角三角形空地中,欲建一个面积不小于 的内接矩形花园(阴影部分),则其边长 (单位 )的取值范围是
A. B. C. D.
8. 某种细胞在培养过程中正常情况下,时刻 (单位:分)与细胞数 (单位:个)的部分数据如下:
根据表中数据,推测繁殖到 个细胞时的时刻 最接近于
A. B. C. D.
9. 客车从甲地以 的速度匀速行驶 小时到达乙地,在乙地停留了半小时,然后以 的速度匀速行驶 小时到达丙地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程 与时间 之间关系的图象中,正确的是
A. B.
C. D.
10. 某商场对顾客实行购物优惠活动,一次购物付款总额:
(1)如果不超过 元,则不给予优惠;
(2)如果超过 元,但不超过 元,则按标价给予 折(即 )优惠;
(3)如果超过 元,其 元内的按第(2)条给予优惠,超过 元的部分给予 折优惠.
某人两次去购物,分别付款 元和 元,假设他一次性购买上述两种同样的商品,则应付款是
A. 元 B. 元 C. 元 D. 元
二、填空题(共5小题;共25分)
11. 某企业年初有资金 万元,若该企业经过有效经营能使每年资金平均增长 ,但每年年底要扣除消费基金 万元,余下投入再生产,为实现 年后资金达 万元(扣除消费基金后),则 .
12. 计算机的价格大约每 年下降 ,那么今年花 元买的一台计算机, 年后的价格大约是 元.
13. 某食品的保鲜时间 (单位:小时)与储藏温度 (单位:)满足函数关系 ( 为自然对数的底数,, 为常数).若该食品在 的保鲜时间是 小时,在 的保鲜时间是 小时,则该食品在 的保鲜时间是 小时.
14. 某种型号的汽车紧急刹车后滑行的距离 与刹车时的速度 的关系可以用 来描述,已知这种型号的汽车在速度为 时,紧急刹车后滑行的距离为 .一辆这种型号的汽车紧急刹车后滑行的距离为 ,则这辆车的行驶速度为 .
15. 已知 , 两地相距 千米,某人开汽车以 的速度从 地到达 地,在 地停留 小时后再以 的速度返回 地,则把汽车离开 地的距离 (千米)表示为时间 (小时)的函数表达式是 .
三、解答题(共3小题;共39分)
16. 有一批影碟机(VCD),原销售价为每台 元,在甲、乙两家家电商场均有销售.甲商场用如下的方法促销:买一台单价为 元,买两台单价都为 元,依此类推,每多买一台则所买各台单价均减少 元,但每台最低不能低于 元;乙商场一律按原价的 销售.某单位需购买一批此类影碟机,问去哪家商场购买花费较少
17. 通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用 表示学生掌握和接受概念的能力( 的值越大,表示接受能力越强), 表示提出和讲授概念的时间(单位:),则有以下关系式:
.
(1)开讲多少分钟后,学生的接受能力最强 能维持多少分钟
(2)一道数学难题,需要 的接受能力以及 的时间,老师能否及时在学生处于所需接受能力的状态下讲授完这道难题
18. 如图设计一幅矩形宣传画,要求画面面积为 ,画面上下边要留 空白,左右要留 空白,怎样确定画面的高与宽的尺寸,才能使宣传画面所用纸张面积最小
答案
第一部分
1. D 【解析】每件获利 元.
2. C
3. C
4. A 【解析】该单位职工每月应缴水费 与实际用水量 满足的关系式为 .
由 ,可知 .
令 ,解得 .
5. C
【解析】设年平均变化率为 ,则 ,, 所求的解析式为 .
6. D 【解析】买小包装时每克费用为 元,买大包装每克费用为 元,而 ,所以买大包装实惠,卖 小包的利润为 (元),卖 大包的利润是 (元).而 ,卖 大包盈利多.
7. C
8. A 【解析】 与 的函数关系式是 .
9. C
10. C
第二部分
11.
【解析】第一年后剩余资金为 ;
第二年剩余资金为 ;
第三年剩余资金为 ,
根据题意,得 ,
解得 .
12.
【解析】 年后的价格是 (元).
13.
【解析】由题可知,, . 当 时,.
14.
15.
【解析】提示:从 地到达 地共用了 小时;从 地到达 地共用 小时.
第三部分
16. 设某单位购买 台影碟机,甲、乙两商场的差价为 ,则去甲商场买共花费 ,由题意
所以 ,去乙商场共花费 ,
①当 时,,
令 且 得 ;
令 且 得 .
令 且 得 .
②当 时,.
则 时,; 时,; 时,.
所以若买少于 台,去乙商场花费较少,若买 台,去甲、乙两商场花费一样,若买多于 台,去甲商场花费较少.
17. (1) 当 时,
.
故当 时,函数 单调递增,故最大值为 .
当 时,.
当 时, 单调递减,且 .
因此,开讲 后,学生达到最强接受能力,能维持 .
(2) 当 时,令 ,解得 ( 舍去).
时,令 ,解得 .
因此学生达到(含超过) 的接受能力时间为 .
故老师来不及在学生处于所需接受能力的状态下讲授完这道难题.
18. 设画面高为 ,宽为 ,
依题意有 ,,,
则所需纸张面积 ,
即 ,
因为 ,,,
所以 ,
当且仅当 ,即 , 时等号成立.
即当画面高为 ,宽为 时,所需纸张面积最小为 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 某种商品进价为每件 元,按进价增加 出售,后因库存积压降价,按九折出售,每件还获利
A. 元 B. 元 C. 元 D. 元
2. 三个变量 随着变量 的变化情况如下表:
则与 呈对数型函数、指数型函数、幂函数型函数变化的变量依次是
A. B. C. D.
3. 某产品的总成本 (万元)与产量 (台)之间的函数关系是 ,若每件产品的售价为 万元,则生产者不亏本时(销售收入不小于总成本)的最低产量为
A. 台 B. 台 C. 台 D. 台
4. 某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过 立方米的,按每立方米 元水费收费;用水超过 立方米的,超过部分按每立方米 元收费.某职工某月缴水费 元,则该职工这个月实际用水为
A. 立方米 B. 立方米 C. 立方米 D. 立方米
5. 据报道,青海的湖水量在最近 年内减少了 ,如果按此规律,设 2010 年的湖水量为 ,从 2010 年起,过 年后湖水量 与 的函数关系式为
A. B.
C. D.
6. 已知每生产100克饼干的原材料加工费为1.8元.某食品加工厂对饼干采用两种包装,其包装费用、销售价格如下表所示:
则下列说法中正确的是
①买小包装实惠 ②买大包装实惠 ③卖 小包比卖 大包盈利多 ④卖 大包比卖 小包盈利多
A. ①③ B. ①④ C. ②③ D. ②④
7. 在如图所示的锐角三角形空地中,欲建一个面积不小于 的内接矩形花园(阴影部分),则其边长 (单位 )的取值范围是
A. B. C. D.
8. 某种细胞在培养过程中正常情况下,时刻 (单位:分)与细胞数 (单位:个)的部分数据如下:
根据表中数据,推测繁殖到 个细胞时的时刻 最接近于
A. B. C. D.
9. 客车从甲地以 的速度匀速行驶 小时到达乙地,在乙地停留了半小时,然后以 的速度匀速行驶 小时到达丙地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程 与时间 之间关系的图象中,正确的是
A. B.
C. D.
10. 某商场对顾客实行购物优惠活动,一次购物付款总额:
(1)如果不超过 元,则不给予优惠;
(2)如果超过 元,但不超过 元,则按标价给予 折(即 )优惠;
(3)如果超过 元,其 元内的按第(2)条给予优惠,超过 元的部分给予 折优惠.
某人两次去购物,分别付款 元和 元,假设他一次性购买上述两种同样的商品,则应付款是
A. 元 B. 元 C. 元 D. 元
二、填空题(共5小题;共25分)
11. 某企业年初有资金 万元,若该企业经过有效经营能使每年资金平均增长 ,但每年年底要扣除消费基金 万元,余下投入再生产,为实现 年后资金达 万元(扣除消费基金后),则 .
12. 计算机的价格大约每 年下降 ,那么今年花 元买的一台计算机, 年后的价格大约是 元.
13. 某食品的保鲜时间 (单位:小时)与储藏温度 (单位:)满足函数关系 ( 为自然对数的底数,, 为常数).若该食品在 的保鲜时间是 小时,在 的保鲜时间是 小时,则该食品在 的保鲜时间是 小时.
14. 某种型号的汽车紧急刹车后滑行的距离 与刹车时的速度 的关系可以用 来描述,已知这种型号的汽车在速度为 时,紧急刹车后滑行的距离为 .一辆这种型号的汽车紧急刹车后滑行的距离为 ,则这辆车的行驶速度为 .
15. 已知 , 两地相距 千米,某人开汽车以 的速度从 地到达 地,在 地停留 小时后再以 的速度返回 地,则把汽车离开 地的距离 (千米)表示为时间 (小时)的函数表达式是 .
三、解答题(共3小题;共39分)
16. 有一批影碟机(VCD),原销售价为每台 元,在甲、乙两家家电商场均有销售.甲商场用如下的方法促销:买一台单价为 元,买两台单价都为 元,依此类推,每多买一台则所买各台单价均减少 元,但每台最低不能低于 元;乙商场一律按原价的 销售.某单位需购买一批此类影碟机,问去哪家商场购买花费较少
17. 通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用 表示学生掌握和接受概念的能力( 的值越大,表示接受能力越强), 表示提出和讲授概念的时间(单位:),则有以下关系式:
.
(1)开讲多少分钟后,学生的接受能力最强 能维持多少分钟
(2)一道数学难题,需要 的接受能力以及 的时间,老师能否及时在学生处于所需接受能力的状态下讲授完这道难题
18. 如图设计一幅矩形宣传画,要求画面面积为 ,画面上下边要留 空白,左右要留 空白,怎样确定画面的高与宽的尺寸,才能使宣传画面所用纸张面积最小
答案
第一部分
1. D 【解析】每件获利 元.
2. C
3. C
4. A 【解析】该单位职工每月应缴水费 与实际用水量 满足的关系式为 .
由 ,可知 .
令 ,解得 .
5. C
【解析】设年平均变化率为 ,则 ,, 所求的解析式为 .
6. D 【解析】买小包装时每克费用为 元,买大包装每克费用为 元,而 ,所以买大包装实惠,卖 小包的利润为 (元),卖 大包的利润是 (元).而 ,卖 大包盈利多.
7. C
8. A 【解析】 与 的函数关系式是 .
9. C
10. C
第二部分
11.
【解析】第一年后剩余资金为 ;
第二年剩余资金为 ;
第三年剩余资金为 ,
根据题意,得 ,
解得 .
12.
【解析】 年后的价格是 (元).
13.
【解析】由题可知,, . 当 时,.
14.
15.
【解析】提示:从 地到达 地共用了 小时;从 地到达 地共用 小时.
第三部分
16. 设某单位购买 台影碟机,甲、乙两商场的差价为 ,则去甲商场买共花费 ,由题意
所以 ,去乙商场共花费 ,
①当 时,,
令 且 得 ;
令 且 得 .
令 且 得 .
②当 时,.
则 时,; 时,; 时,.
所以若买少于 台,去乙商场花费较少,若买 台,去甲、乙两商场花费一样,若买多于 台,去甲商场花费较少.
17. (1) 当 时,
.
故当 时,函数 单调递增,故最大值为 .
当 时,.
当 时, 单调递减,且 .
因此,开讲 后,学生达到最强接受能力,能维持 .
(2) 当 时,令 ,解得 ( 舍去).
时,令 ,解得 .
因此学生达到(含超过) 的接受能力时间为 .
故老师来不及在学生处于所需接受能力的状态下讲授完这道难题.
18. 设画面高为 ,宽为 ,
依题意有 ,,,
则所需纸张面积 ,
即 ,
因为 ,,,
所以 ,
当且仅当 ,即 , 时等号成立.
即当画面高为 ,宽为 时,所需纸张面积最小为 .
第1页(共1 页)
