数学人教版六年级下册5.1《鸽巢问题》(1)课件(共20张PPT)
文档属性
| 名称 | 数学人教版六年级下册5.1《鸽巢问题》(1)课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 28.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 09:45:14 | ||
图片预览




文档简介
(共20张PPT)
鸽巢问题(1)
人教版 六年级下册
学习目标
理解“总有”“至少”的意义,理解“至少数=商+1”。
理解鸽巢原理,掌握先“平均分”,再调整的方法。
了解什么是鸽巢原理,学会简单的鸽巢原理分析方法。
我给大家表演一个“魔术”。
一副牌,取出大小王,还剩52张牌。
你们5人每人随意抽一张,我知道至少有两张牌是同花色的。相信吗?
情境导入
情境导入
新课讲解
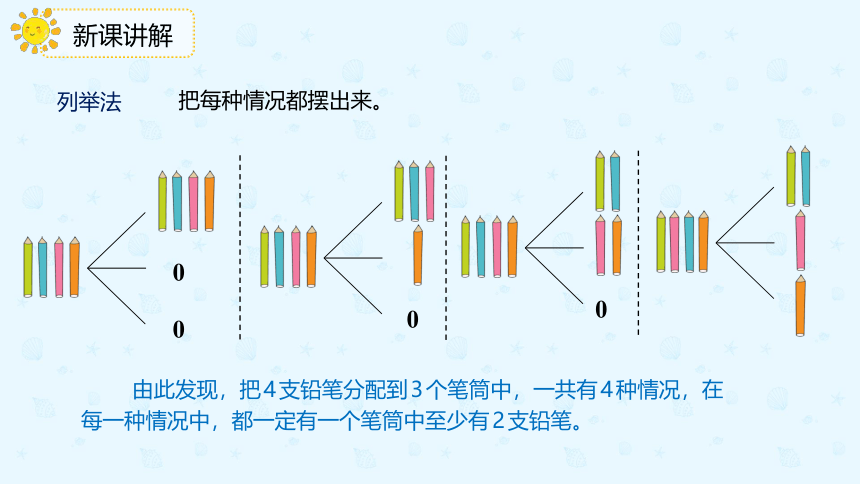
列举法
0
0
0
0
把每种情况都摆出来。
由此发现,把4支铅笔分配到3个笔筒中,一共有4种情况,在每一种情况中,都一定有一个笔筒中至少有2支铅笔。
新课讲解
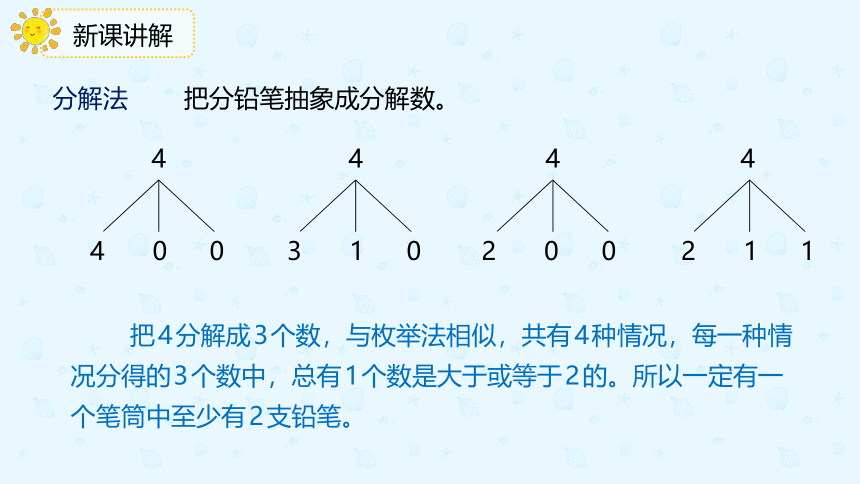
分解法
把分铅笔抽象成分解数。
4
4
0
0
4
3
1
0
4
2
0
0
4
2
1
1
把4分解成3个数,与枚举法相似,共有4种情况,每一种情况分得的3个数中,总有1个数是大于或等于2的。所以一定有一个笔筒中至少有2支铅笔。
先放 3 支,在每个笔筒中放 1 支,剩下的 1 支就要放进其中的一个笔筒。所以至少有一个笔筒中有 2 支铅笔。
新课讲解
假设法
新课讲解
新课讲解
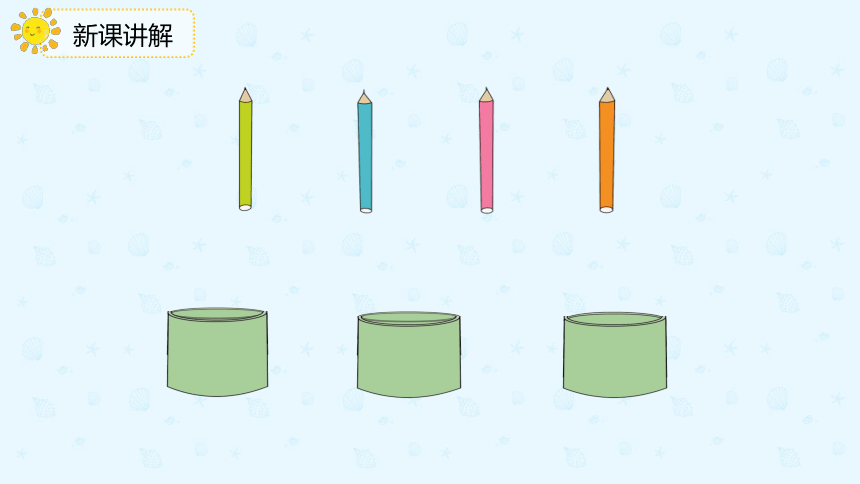
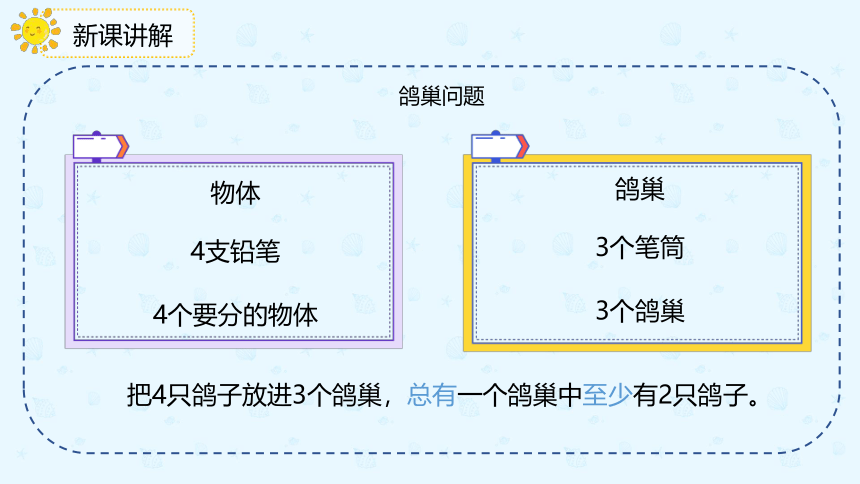
鸽巢问题
物体
4支铅笔
4个要分的物体
鸽巢
3个笔筒
3个鸽巢
把4只鸽子放进3个鸽巢,总有一个鸽巢中至少有2只鸽子。
新课讲解
小结(1):
鸽巢原理(也叫抽屉原理)
把m个物体任意放进n个鸽巢(抽屉)中,(m>n,m和n是非0的自然数,)若m÷n=1······a,那么一定有一个鸽巢问(抽屉)中至少放进了2个物体。
新课讲解
小结(2):
鸽巢问题的一般形式
把m个物体任意放进n个鸽巢(抽屉)中,(m>n),如果m÷n=k······b,那么总有一个抽屉放入(k+1)个物体。
课堂练习
(1)5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了两只鸽子。为什么?
如果每个鸽笼只飞进1只鸽子,最多能飞进3只鸽子,剩下的2只鸽子还要飞进任意一个鸽笼里,所以至少有2只鸽子要飞进同一鸽笼。
课堂练习
(2)选8个小朋友分35块糖,总有一个小朋友至少分得几糖?
求至少数用商+1计算。
35÷8=4(块)······3(块)
4+1=5(块)
答:总有一个小朋友至少分得5块糖。
课堂练习
(3)张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于9环。为什么?
看作5个抽屉。
41÷5=8(环)······1(环)
8+1=9(块)
这道题相当于把41环分到5个抽屉中,必有一个抽屉至少有9环。
课堂练习
(4)11只鸽子飞进了4个鸽笼,总有一个鸽笼至少进了3只鸽子。为什么?
11÷4=2(只)······3(只)
2+1=3(只)
因为平均每个鸽笼都飞进了2只鸽子,还剩下3只,不论怎么飞,总有1个鸽笼里至少飞进3只鸽子。
课堂练习
(5)5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
5÷4=1(人)······1(人)
1+1=2(人)
因为平均每把椅子上都坐一个人,还剩下1人,不论怎么坐,总有1把椅子上至少坐2人。
课堂练习
(6)把若干枝花插入5个花瓶里,不管怎么放,要保证总有一个花瓶里至少插10枝花,那么花的总数至少应该有多少枝?
5个花瓶:抽屉数
物体的个数比抽屉数多1。
5×(10-1)+1=46(枝)
答:花的总数至少应该有46枝。
插10枝花:物体的个数
课堂小结
鸽巢原理(也叫抽屉原理):
把m个物体任意放进n个鸽巢(抽屉)中,(m>n,m和n是非0的自然数,)若m÷n=1······a,那么一定有一个鸽巢问(抽屉)中至少放进了2个物体。
鸽巢问题的一般形式:
把m个物体任意放进n个鸽巢(抽屉)中,(m>n),如果m÷n=k······b,那么总有一个抽屉放入(k+1)个物体。
1、课后练习:9、11题
2、练习册:《鸽巢问题(1)》
课后作业
感 谢 聆 听
人教版 六年级下册
注:本课件所有素材来源于网络,如有侵权,请联系我们。
鸽巢问题(1)
人教版 六年级下册
学习目标
理解“总有”“至少”的意义,理解“至少数=商+1”。
理解鸽巢原理,掌握先“平均分”,再调整的方法。
了解什么是鸽巢原理,学会简单的鸽巢原理分析方法。
我给大家表演一个“魔术”。
一副牌,取出大小王,还剩52张牌。
你们5人每人随意抽一张,我知道至少有两张牌是同花色的。相信吗?
情境导入
情境导入
新课讲解
列举法
0
0
0
0
把每种情况都摆出来。
由此发现,把4支铅笔分配到3个笔筒中,一共有4种情况,在每一种情况中,都一定有一个笔筒中至少有2支铅笔。
新课讲解
分解法
把分铅笔抽象成分解数。
4
4
0
0
4
3
1
0
4
2
0
0
4
2
1
1
把4分解成3个数,与枚举法相似,共有4种情况,每一种情况分得的3个数中,总有1个数是大于或等于2的。所以一定有一个笔筒中至少有2支铅笔。
先放 3 支,在每个笔筒中放 1 支,剩下的 1 支就要放进其中的一个笔筒。所以至少有一个笔筒中有 2 支铅笔。
新课讲解
假设法
新课讲解
新课讲解
鸽巢问题
物体
4支铅笔
4个要分的物体
鸽巢
3个笔筒
3个鸽巢
把4只鸽子放进3个鸽巢,总有一个鸽巢中至少有2只鸽子。
新课讲解
小结(1):
鸽巢原理(也叫抽屉原理)
把m个物体任意放进n个鸽巢(抽屉)中,(m>n,m和n是非0的自然数,)若m÷n=1······a,那么一定有一个鸽巢问(抽屉)中至少放进了2个物体。
新课讲解
小结(2):
鸽巢问题的一般形式
把m个物体任意放进n个鸽巢(抽屉)中,(m>n),如果m÷n=k······b,那么总有一个抽屉放入(k+1)个物体。
课堂练习
(1)5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了两只鸽子。为什么?
如果每个鸽笼只飞进1只鸽子,最多能飞进3只鸽子,剩下的2只鸽子还要飞进任意一个鸽笼里,所以至少有2只鸽子要飞进同一鸽笼。
课堂练习
(2)选8个小朋友分35块糖,总有一个小朋友至少分得几糖?
求至少数用商+1计算。
35÷8=4(块)······3(块)
4+1=5(块)
答:总有一个小朋友至少分得5块糖。
课堂练习
(3)张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于9环。为什么?
看作5个抽屉。
41÷5=8(环)······1(环)
8+1=9(块)
这道题相当于把41环分到5个抽屉中,必有一个抽屉至少有9环。
课堂练习
(4)11只鸽子飞进了4个鸽笼,总有一个鸽笼至少进了3只鸽子。为什么?
11÷4=2(只)······3(只)
2+1=3(只)
因为平均每个鸽笼都飞进了2只鸽子,还剩下3只,不论怎么飞,总有1个鸽笼里至少飞进3只鸽子。
课堂练习
(5)5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
5÷4=1(人)······1(人)
1+1=2(人)
因为平均每把椅子上都坐一个人,还剩下1人,不论怎么坐,总有1把椅子上至少坐2人。
课堂练习
(6)把若干枝花插入5个花瓶里,不管怎么放,要保证总有一个花瓶里至少插10枝花,那么花的总数至少应该有多少枝?
5个花瓶:抽屉数
物体的个数比抽屉数多1。
5×(10-1)+1=46(枝)
答:花的总数至少应该有46枝。
插10枝花:物体的个数
课堂小结
鸽巢原理(也叫抽屉原理):
把m个物体任意放进n个鸽巢(抽屉)中,(m>n,m和n是非0的自然数,)若m÷n=1······a,那么一定有一个鸽巢问(抽屉)中至少放进了2个物体。
鸽巢问题的一般形式:
把m个物体任意放进n个鸽巢(抽屉)中,(m>n),如果m÷n=k······b,那么总有一个抽屉放入(k+1)个物体。
1、课后练习:9、11题
2、练习册:《鸽巢问题(1)》
课后作业
感 谢 聆 听
人教版 六年级下册
注:本课件所有素材来源于网络,如有侵权,请联系我们。
