数学人教版六年级下册6.1.3《式与方程》课件(共21张PPT)
文档属性
| 名称 | 数学人教版六年级下册6.1.3《式与方程》课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 26.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第三课时
式与方程
人教版 六年级下册
学习目标
培养学生用字母表示数的意识和兴趣,使学生产生对数学学习的好奇心。
通过教学的过程,使学生能正确解方程,解题能力得到提高。
使学生掌握用字母表示数和常见的数量关系;会根据字母所取的值,求含有字母的式子的值。
方程这个名词,最早见于我国古代算书《九章算术》。《九章算术》是在我国东汉初年编定的一部现有传本的、最古老的中国数学经典著作.书中收集了246个应用问题和其他问题的解法,分为九章,“方程”是其中的一章。
“方程”一词是中国发明的词汇,但方程本身却不是发源于中国。
十六世纪,随着各种数学符号的相继出现,特别是法国数学家韦达创立了较系统的表示未知量和已知量的符号后,“方程”这一专门的概念就出现了
可用特殊的字母表示
情境导入
字母表示数为研究和解决问题带来很多方便,
简明地表达数量、数量关系
运算定律
计算公式
那就一起学习吧!
新课讲解
用字母
表示数
用字母表示数量关系
用字母表示运算定律
用字母表示计算公式
用字母表示计算方法
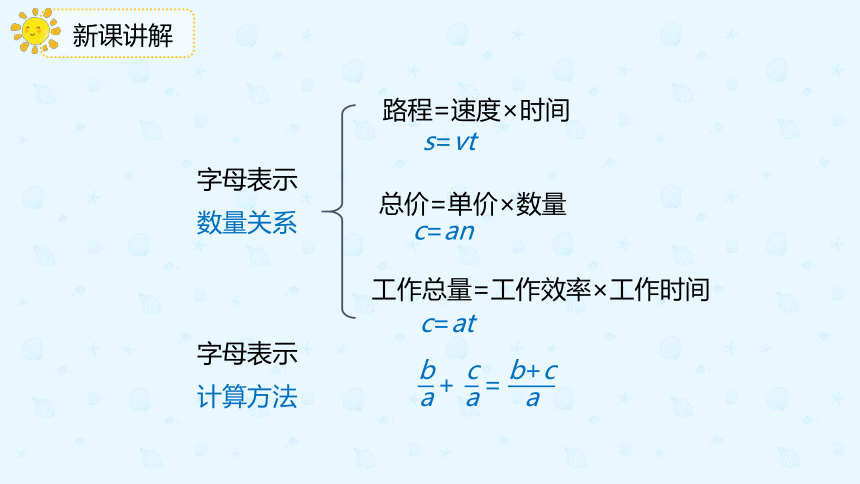
新课讲解
路程=速度×时间
s=vt
总价=单价×数量
c=an
字母表示 数量关系
字母表示
计算方法
+
=
工作总量=工作效率×工作时间
c=at
新课讲解
名称 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
举手回答:说一说运算定律用字母该怎样表示?
新课讲解
举手回答:在一个含有字母的式子里,数与字母、字母与字母相乘,书写时应注意什么?
在含有字母的式子里,数和字母中间的乘号可以用“ ”代替,也可以省略不写。
省略乘号时,应当把数写在字母的前面。
数与数之间的乘号不能省略。加号、减号、除号都不能省略。
新课讲解
方程
方程的意义:
方程与等式的关系:
解方程:
含有未知数的等式叫作方程。
方程
等式
求方程解的过程叫作解方程。
新课讲解
方程与等式的联系和区别
所有的方程都是等式,等式包括方程。
联系
所有的等式不一定是方程,等式范围更大;等式不一定含有未知数,方程必须含有未知数。
区别
新课讲解
2.5 + x = 5.3
解:2.5-2.5 +x = 5.3-2.5
x = 2.8
等式的性质1:等式两边同时加上或减去同一个数,等式仍然成立。
解: x ÷10×10 = 12.5×10
x÷10 = 12.5
x = 125
小组交流:试着举例说明等式的性质
等式的性质2:等式两边同时乘或除以同一个数(0除外),等式仍然成立。
新课讲解
用方程解决问题的步骤
审题,理解题意;
1
找出等量关系;
2
根据等量关系列方程;
3
解方程;
4
检验写答语。
5
新课讲解
列方程解决实际问题的类型
是一个数的几倍(或几分之几);比一个数的几倍少几(或几倍多几)的数是多少的实际问题。
1
行程问题。
2
和倍问题或差倍问题。
3
年龄问题。
4
综合问题。
5
新课讲解
比a多3的数
比a少3的数
3个a相加的和
3个a相乘的积
a的3倍
a的
a3
3a
a+3
a-3
连一连。
课堂练习
1.李奶奶家本月用电a千瓦时,比上个月多用10千瓦时,上个月用电
( )千瓦时。
2.如果每千瓦时电的价格是c元,李奶奶家本月的电费是( )元。
李奶奶家银行缴费卡上原有215元,扣除本月电费后,还剩( )元。
3.三个连续的自然数,最大的一个是n,那么最小的一个数是( )。
a-10
ac
215-ac
n-2
填一填。
课堂练习
6x+20% = 24.2
解:6x+0.2-0.2 = 24.2-0.2
6x=24
x=4
x
x
-
= 32
解:( - )x=32
x=32
x÷
=32÷
x=64
6x÷6=24÷6
解方程。
课堂练在踢毽子比赛中踢了42下,她踢毽子的数量是小云的 。小云踢了多少下?
小云踢的下数× =小平踢的下数
解:设小云踢了x下。
x=42
x ÷ =42 ÷
x=56
答:小云踢了56下。
课堂练习
一台数码摄像机的价格是8800元,比一台数码照相机的价格的3倍少200元。一台数码照相机的价格是多少元?
解:设一台数码照相机的价格是x元。
3 x -200=8800
3 x -200+200=8800+200
3 x =9000
x =3000
答:一台数码照相机的价格是3000元。
照相机的价格×3-200 =数码摄像机的价格
课堂练习
课堂小结
方程与等式的联系和区别
所有的方程都是等式,等式包括方程。
联系
所有的等式不一定是方程,等式范围更大;等式不一定含有未知数,方程必须含有未知数。
区别
课后作业
1、从教材课后习题中选取2、从课时练中选取
感 谢 聆 听
人教版 六年级下册
注:本视频所有素材来源于网络,如有侵权,请联系我们。
第三课时
式与方程
人教版 六年级下册
学习目标
培养学生用字母表示数的意识和兴趣,使学生产生对数学学习的好奇心。
通过教学的过程,使学生能正确解方程,解题能力得到提高。
使学生掌握用字母表示数和常见的数量关系;会根据字母所取的值,求含有字母的式子的值。
方程这个名词,最早见于我国古代算书《九章算术》。《九章算术》是在我国东汉初年编定的一部现有传本的、最古老的中国数学经典著作.书中收集了246个应用问题和其他问题的解法,分为九章,“方程”是其中的一章。
“方程”一词是中国发明的词汇,但方程本身却不是发源于中国。
十六世纪,随着各种数学符号的相继出现,特别是法国数学家韦达创立了较系统的表示未知量和已知量的符号后,“方程”这一专门的概念就出现了
可用特殊的字母表示
情境导入
字母表示数为研究和解决问题带来很多方便,
简明地表达数量、数量关系
运算定律
计算公式
那就一起学习吧!
新课讲解
用字母
表示数
用字母表示数量关系
用字母表示运算定律
用字母表示计算公式
用字母表示计算方法
新课讲解
路程=速度×时间
s=vt
总价=单价×数量
c=an
字母表示 数量关系
字母表示
计算方法
+
=
工作总量=工作效率×工作时间
c=at
新课讲解
名称 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
举手回答:说一说运算定律用字母该怎样表示?
新课讲解
举手回答:在一个含有字母的式子里,数与字母、字母与字母相乘,书写时应注意什么?
在含有字母的式子里,数和字母中间的乘号可以用“ ”代替,也可以省略不写。
省略乘号时,应当把数写在字母的前面。
数与数之间的乘号不能省略。加号、减号、除号都不能省略。
新课讲解
方程
方程的意义:
方程与等式的关系:
解方程:
含有未知数的等式叫作方程。
方程
等式
求方程解的过程叫作解方程。
新课讲解
方程与等式的联系和区别
所有的方程都是等式,等式包括方程。
联系
所有的等式不一定是方程,等式范围更大;等式不一定含有未知数,方程必须含有未知数。
区别
新课讲解
2.5 + x = 5.3
解:2.5-2.5 +x = 5.3-2.5
x = 2.8
等式的性质1:等式两边同时加上或减去同一个数,等式仍然成立。
解: x ÷10×10 = 12.5×10
x÷10 = 12.5
x = 125
小组交流:试着举例说明等式的性质
等式的性质2:等式两边同时乘或除以同一个数(0除外),等式仍然成立。
新课讲解
用方程解决问题的步骤
审题,理解题意;
1
找出等量关系;
2
根据等量关系列方程;
3
解方程;
4
检验写答语。
5
新课讲解
列方程解决实际问题的类型
是一个数的几倍(或几分之几);比一个数的几倍少几(或几倍多几)的数是多少的实际问题。
1
行程问题。
2
和倍问题或差倍问题。
3
年龄问题。
4
综合问题。
5
新课讲解
比a多3的数
比a少3的数
3个a相加的和
3个a相乘的积
a的3倍
a的
a3
3a
a+3
a-3
连一连。
课堂练习
1.李奶奶家本月用电a千瓦时,比上个月多用10千瓦时,上个月用电
( )千瓦时。
2.如果每千瓦时电的价格是c元,李奶奶家本月的电费是( )元。
李奶奶家银行缴费卡上原有215元,扣除本月电费后,还剩( )元。
3.三个连续的自然数,最大的一个是n,那么最小的一个数是( )。
a-10
ac
215-ac
n-2
填一填。
课堂练习
6x+20% = 24.2
解:6x+0.2-0.2 = 24.2-0.2
6x=24
x=4
x
x
-
= 32
解:( - )x=32
x=32
x÷
=32÷
x=64
6x÷6=24÷6
解方程。
课堂练在踢毽子比赛中踢了42下,她踢毽子的数量是小云的 。小云踢了多少下?
小云踢的下数× =小平踢的下数
解:设小云踢了x下。
x=42
x ÷ =42 ÷
x=56
答:小云踢了56下。
课堂练习
一台数码摄像机的价格是8800元,比一台数码照相机的价格的3倍少200元。一台数码照相机的价格是多少元?
解:设一台数码照相机的价格是x元。
3 x -200=8800
3 x -200+200=8800+200
3 x =9000
x =3000
答:一台数码照相机的价格是3000元。
照相机的价格×3-200 =数码摄像机的价格
课堂练习
课堂小结
方程与等式的联系和区别
所有的方程都是等式,等式包括方程。
联系
所有的等式不一定是方程,等式范围更大;等式不一定含有未知数,方程必须含有未知数。
区别
课后作业
1、从教材课后习题中选取2、从课时练中选取
感 谢 聆 听
人教版 六年级下册
注:本视频所有素材来源于网络,如有侵权,请联系我们。
