数学人教版六年级下册4.3.6《用比例解决问题(2)》课件(共21张PPT)
文档属性
| 名称 | 数学人教版六年级下册4.3.6《用比例解决问题(2)》课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 26.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
用比例解决问题(2)
人教版 六年级下册
学习目标
根据题目意思确定用哪种方法解决问题。
能正确运用比例知识解决问题,发展学生的应用意思和实际能力。
使学生掌握运用比例解决问题的方法。能正确运用比例知识解决问题,发展学生的应用意思和实际能力。
复习导入
下面各题中的两种量是否成比例,成什么比例?
(1)比例尺一定,图上距离和实际距离。
(2)工作总量一定,工作效率和工作时间。
(3)总路程一定,已行的路程和剩下的路程。
(4)平行四边形的面积一定,平行四边形的底和对应的高。
正比例
反比例
不成比例
反比例
复习导入
光辉服装厂4天加工服装160套,照这样计算,生产360套服装,需要多少天?(用比例解答)
解:设生产360套服装需要X天。
4
160
=
X
360
160X=360×4
答:生产360套服装需要9天。
X=9
新课讲解
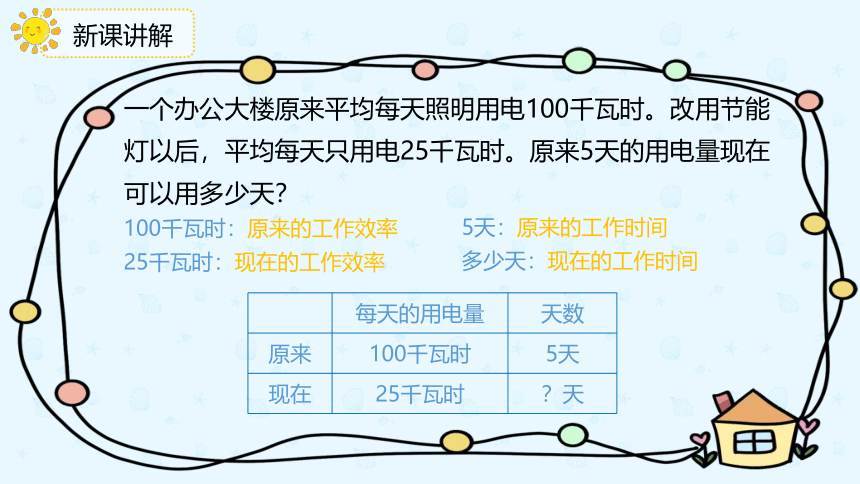
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
100千瓦时:原来的工作效率
25千瓦时:现在的工作效率
5天:原来的工作时间
多少天:现在的工作时间
每天的用电量 天数
原来 100千瓦时 5天
现在 25千瓦时 ?天
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
算术法:
先求原来5天的用电量。
100×5=500(千瓦时)
再求现在可以用的天数。
500÷25=20(天)
100×5÷25
=500÷25
=20(天)
答:原来5天的用电量现在可以用20天。
新课讲解
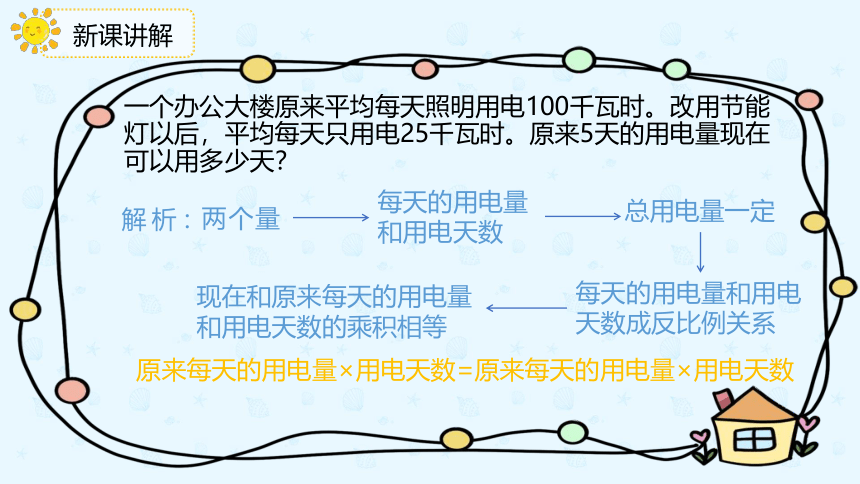
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
原来每天的用电量×用电天数=原来每天的用电量×用电天数
解析:
两个量
每天的用电量和用电天数
总用电量一定
每天的用电量和用电天数成反比例关系
现在和原来每天的用电量和用电天数的乘积相等
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
用比例
的方法:
解:设原来5天用的电量现在可以用X天。
X=20
现在用
电总量
原来用
电总量
答:原来5天的用电量现在可以用20天。
25X=100×5
新课讲解
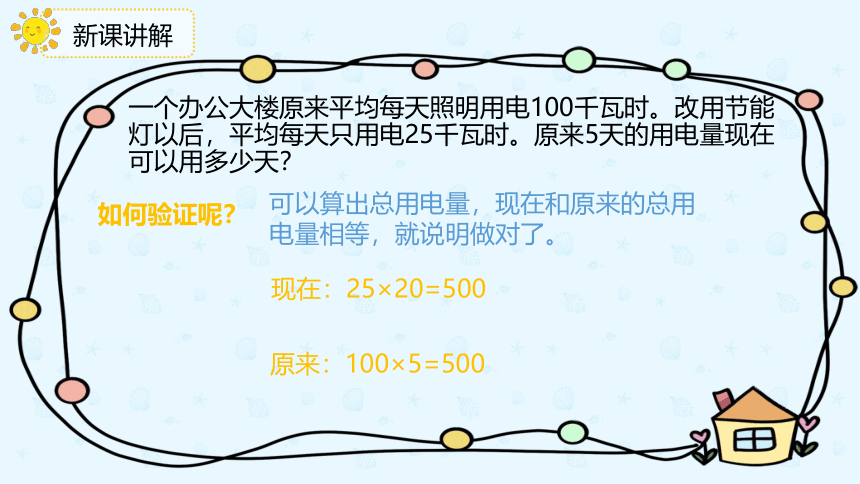
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
如何验证呢?
可以算出总用电量,现在和原来的总用电量相等,就说明做对了。
现在:25×20=500
原来:100×5=500
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来30天的用电量现在可以用多少天?
解:设原来30天用的电量现在可以用X天。
X=7.5
答:原来30天的用电量现在可以用7.5天。
100X=25×30
新课讲解
用正、反比例知识解决问题的异同点
相同
都是用比例的知识解答,解题思路相同。
不相同
用正比例知识解决问题是根据比值一定列出比例,
用反比例知识解决问题是根据积一定列出比例。
新课讲解
用比例解决问题的一般步骤
(1)根据不变量判断题中哪两种相关联的量成比例关系。
(2)找出两组相对应的数,并设出未知数,列出方程。
(3)解方程。
(4)检验并写出答语。
课堂练习
1.学校小商店有两种圆珠笔,小明带的钱刚好可以买4支单价是1.5元的,如果他只买单价是2元的,可以买多少支?
总价一定,单价和数量成反比例关系。
解:设如果只买单价2元的,可以买X支。
X=3
答:如果只买单价2元的,可以买3支。
2X=4×1.5
课堂练习
2.小明家用收割收割机小麦。如果每小时收割0.3公顷,40小时能完成任务。现在想用30小时收割完,那么每小时应收割多少公顷?
工作总量一定,工作时间和工作效率成反比例关系。
解:设每小时应收割X公顷。
X=0.4
答:每小时应收割0.4公顷。
30X=0.3×40
课堂练习
3.工程队修一条水渠,每天工作6小时,12天可以完成任务。如果工作效率不变,每天工作8小时,多少天可以完成任务?
解:设X天可以完成任务。
X=9
答:9天可以完成任务。
8X=6×12
课堂练习
4.一辆运货汽车从甲地开往乙地,平均每小时行72km,10小时到达。回来时空车原路返回,每小时可行90km。多长时间能够返回原地?
解:设X小时能够返回原地。
X=8
答:8小时能够返回原地。
90X=72×10
课堂练习
5.填空。
(1)比例尺一定,实际距离和图上距离成( )比例。
(2)如果X÷Y=6.5×4,那么X和Y成( )比例。
(3)如果4:X=5:Y,那么X和Y成( )比例。
正
正
正
课堂练习
6.小红的身高是1.6m,她的影长是2.5m,如果同一时间、同一地点测得一棵树的影长4m,那么这棵树有多高?
解:设这棵树有Xm高。
X=2.56
答:这棵树有2.56m高。
1.6:2.5=X:4
课堂小结
分析题意,弄清两个相关联的量积不变还是商不变。
用正比例知识解决问题是根据比值一定列出比例,用反比例知识解决问题是根据积一定列出比例
1、课后练习:第9、11题
2、练习册:用比例解决问题(2)
课后作业
感 谢 聆 听
人教版 六年级下册
注:本课件所有素材来源于网络,如有侵权,请联系我们。
用比例解决问题(2)
人教版 六年级下册
学习目标
根据题目意思确定用哪种方法解决问题。
能正确运用比例知识解决问题,发展学生的应用意思和实际能力。
使学生掌握运用比例解决问题的方法。能正确运用比例知识解决问题,发展学生的应用意思和实际能力。
复习导入
下面各题中的两种量是否成比例,成什么比例?
(1)比例尺一定,图上距离和实际距离。
(2)工作总量一定,工作效率和工作时间。
(3)总路程一定,已行的路程和剩下的路程。
(4)平行四边形的面积一定,平行四边形的底和对应的高。
正比例
反比例
不成比例
反比例
复习导入
光辉服装厂4天加工服装160套,照这样计算,生产360套服装,需要多少天?(用比例解答)
解:设生产360套服装需要X天。
4
160
=
X
360
160X=360×4
答:生产360套服装需要9天。
X=9
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
100千瓦时:原来的工作效率
25千瓦时:现在的工作效率
5天:原来的工作时间
多少天:现在的工作时间
每天的用电量 天数
原来 100千瓦时 5天
现在 25千瓦时 ?天
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
算术法:
先求原来5天的用电量。
100×5=500(千瓦时)
再求现在可以用的天数。
500÷25=20(天)
100×5÷25
=500÷25
=20(天)
答:原来5天的用电量现在可以用20天。
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
原来每天的用电量×用电天数=原来每天的用电量×用电天数
解析:
两个量
每天的用电量和用电天数
总用电量一定
每天的用电量和用电天数成反比例关系
现在和原来每天的用电量和用电天数的乘积相等
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
用比例
的方法:
解:设原来5天用的电量现在可以用X天。
X=20
现在用
电总量
原来用
电总量
答:原来5天的用电量现在可以用20天。
25X=100×5
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
如何验证呢?
可以算出总用电量,现在和原来的总用电量相等,就说明做对了。
现在:25×20=500
原来:100×5=500
新课讲解
一个办公大楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来30天的用电量现在可以用多少天?
解:设原来30天用的电量现在可以用X天。
X=7.5
答:原来30天的用电量现在可以用7.5天。
100X=25×30
新课讲解
用正、反比例知识解决问题的异同点
相同
都是用比例的知识解答,解题思路相同。
不相同
用正比例知识解决问题是根据比值一定列出比例,
用反比例知识解决问题是根据积一定列出比例。
新课讲解
用比例解决问题的一般步骤
(1)根据不变量判断题中哪两种相关联的量成比例关系。
(2)找出两组相对应的数,并设出未知数,列出方程。
(3)解方程。
(4)检验并写出答语。
课堂练习
1.学校小商店有两种圆珠笔,小明带的钱刚好可以买4支单价是1.5元的,如果他只买单价是2元的,可以买多少支?
总价一定,单价和数量成反比例关系。
解:设如果只买单价2元的,可以买X支。
X=3
答:如果只买单价2元的,可以买3支。
2X=4×1.5
课堂练习
2.小明家用收割收割机小麦。如果每小时收割0.3公顷,40小时能完成任务。现在想用30小时收割完,那么每小时应收割多少公顷?
工作总量一定,工作时间和工作效率成反比例关系。
解:设每小时应收割X公顷。
X=0.4
答:每小时应收割0.4公顷。
30X=0.3×40
课堂练习
3.工程队修一条水渠,每天工作6小时,12天可以完成任务。如果工作效率不变,每天工作8小时,多少天可以完成任务?
解:设X天可以完成任务。
X=9
答:9天可以完成任务。
8X=6×12
课堂练习
4.一辆运货汽车从甲地开往乙地,平均每小时行72km,10小时到达。回来时空车原路返回,每小时可行90km。多长时间能够返回原地?
解:设X小时能够返回原地。
X=8
答:8小时能够返回原地。
90X=72×10
课堂练习
5.填空。
(1)比例尺一定,实际距离和图上距离成( )比例。
(2)如果X÷Y=6.5×4,那么X和Y成( )比例。
(3)如果4:X=5:Y,那么X和Y成( )比例。
正
正
正
课堂练习
6.小红的身高是1.6m,她的影长是2.5m,如果同一时间、同一地点测得一棵树的影长4m,那么这棵树有多高?
解:设这棵树有Xm高。
X=2.56
答:这棵树有2.56m高。
1.6:2.5=X:4
课堂小结
分析题意,弄清两个相关联的量积不变还是商不变。
用正比例知识解决问题是根据比值一定列出比例,用反比例知识解决问题是根据积一定列出比例
1、课后练习:第9、11题
2、练习册:用比例解决问题(2)
课后作业
感 谢 聆 听
人教版 六年级下册
注:本课件所有素材来源于网络,如有侵权,请联系我们。
