5.1.1 变化率问题 2021-2022学年高二下学期同步课件(人教A版2019选择性必修第二册)(30张ppt)
文档属性
| 名称 | 5.1.1 变化率问题 2021-2022学年高二下学期同步课件(人教A版2019选择性必修第二册)(30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 871.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-16 12:41:54 | ||
图片预览




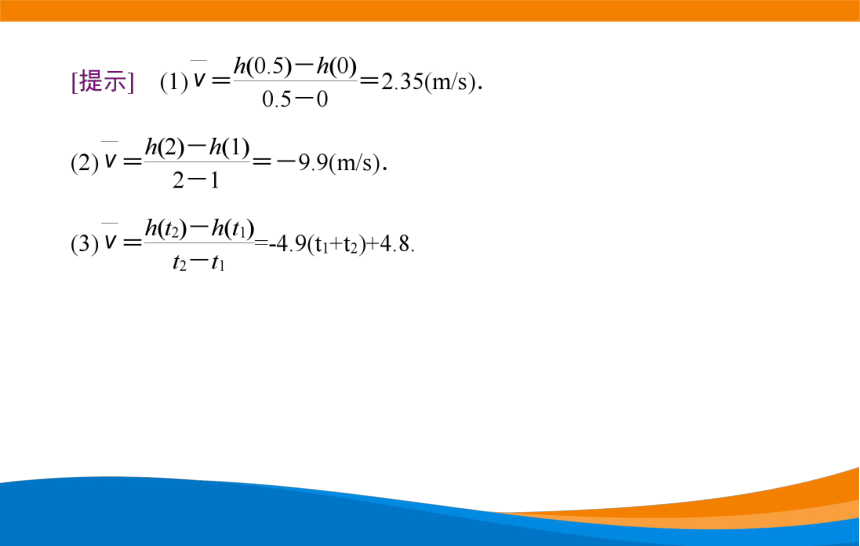





文档简介
(共30张PPT)
第五章
一元函数的导数及其应用
5.1 导数的概念及其意义
5.1.1 变化率问题
思考:在0≤t≤这段时间里,运动员的平均速度是多少?
提示:在0≤t≤这段时间里,运动员的平均速度是0
思考:平均速度是0,是否意味着运动在这段时间内是静止的呢?
提示:不是,运动员是运动的
思考:那怎么来描述运动员在这段时间内的运动状态呢?
提示:用瞬时速度来描述运动员在这段时间内的运动状态
某一时刻
×
√
×
×
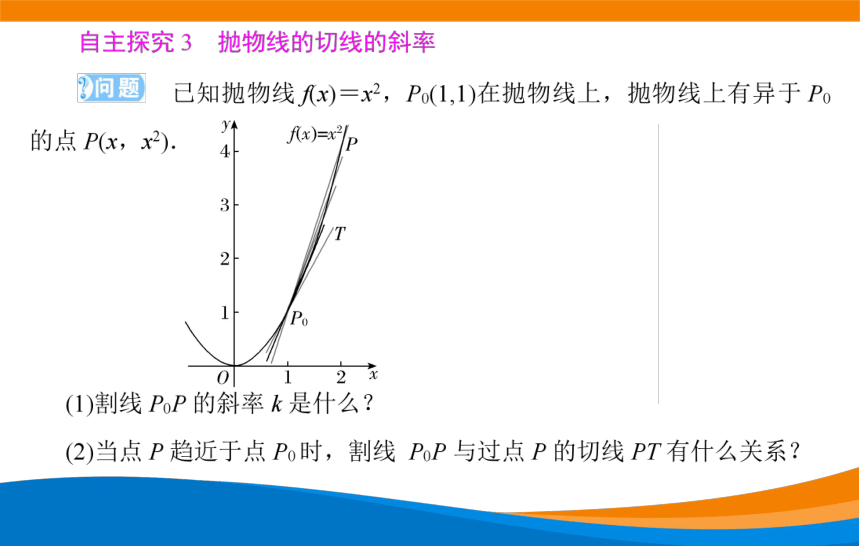
(3)记△x=x-1,则点P的坐标为(1+△x,(1+△x)2)。
于是割线P0P的斜率k=;
从几何图形上看,当横坐标的间隔|△x|无限小时,点P无限趋近于点P0,
于是割线P0P无限趋近于点P0处的切线P0T。
这时割线P0P的斜率k无限趋近于点P0处的切线P0T。
因此,切线P0T的斜率k0=
◎结论形成
函数f(x)在点(x0,f(x0))处的切线斜率k=
在该点处的切线l的方程为:y-f(x0)=k(x-x0).
2022/1/14
【题型探究】
THANKS FOR YOUR LISTENING
f(a
K=n
2
结论形成
第五章
一元函数的导数及其应用
5.1 导数的概念及其意义
5.1.1 变化率问题
思考:在0≤t≤这段时间里,运动员的平均速度是多少?
提示:在0≤t≤这段时间里,运动员的平均速度是0
思考:平均速度是0,是否意味着运动在这段时间内是静止的呢?
提示:不是,运动员是运动的
思考:那怎么来描述运动员在这段时间内的运动状态呢?
提示:用瞬时速度来描述运动员在这段时间内的运动状态
某一时刻
×
√
×
×
(3)记△x=x-1,则点P的坐标为(1+△x,(1+△x)2)。
于是割线P0P的斜率k=;
从几何图形上看,当横坐标的间隔|△x|无限小时,点P无限趋近于点P0,
于是割线P0P无限趋近于点P0处的切线P0T。
这时割线P0P的斜率k无限趋近于点P0处的切线P0T。
因此,切线P0T的斜率k0=
◎结论形成
函数f(x)在点(x0,f(x0))处的切线斜率k=
在该点处的切线l的方程为:y-f(x0)=k(x-x0).
2022/1/14
【题型探究】
THANKS FOR YOUR LISTENING
f(a
K=n
2
结论形成
