2022版高中数学第二章函数本章达标检测含解析北师大版必修1(word版含解析)
文档属性
| 名称 | 2022版高中数学第二章函数本章达标检测含解析北师大版必修1(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 115.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-15 08:17:17 | ||
图片预览




文档简介
第二章 函数
本章达标检测
(满分:150分;时间:120分钟)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设α∈-1,,1,2,3,使函数y=xα的定义域为R且为奇函数的所有α的值为 ( )
A.1,3 B.1,2
C.2,3 D.-1,1,3
2.下列函数中,既是偶函数又在区间(0,+∞)上是增函数的是 ( )
A.y=|x| B.y=3-x
C.y= D.y=-x2+4
3.二次函数f(x)=ax2+bx+8满足条件f(-1)=f(3),则f(2)的值为 ( )
A.5 B.6
C.8 D.与a,b值有关
4.函数f(x)=(x+2)2+mx+1是偶函数,则m= ( )
A.0 B.2
C.4 D.-4
5.已知f=2x-5,且f(a)=6,则a等于 ( )
A.- B.
C. D.-
6.已知函数f(x)=的定义域是一切实数,则m的取值范围是 ( )
A.0C.m≥4 D.0≤m≤4
7.已知奇函数f(x)在(-∞,+∞)上单调递减,若f(1)=-2,则满足f(x-1)≤2的x的取值区间是 ( )
A.[0,+∞) B.(-∞,0]
C.[2,+∞) D.(-∞,2]
8.已知定义域为R的函数f(x)满足f(3-x)=f(x+1),当x≥2时,f(x)单调递减,且f(a)≥f(0),则实数a的取值范围是( )
A.[2,+∞) B.[0,4]
C.(-∞,0) D.(-∞,0)∪[4,+∞)
9.函数f(x)=2+3x在区间[-1,1]上的最大值为 ( )
A.2 B.3+2
C.13-4 D.-4
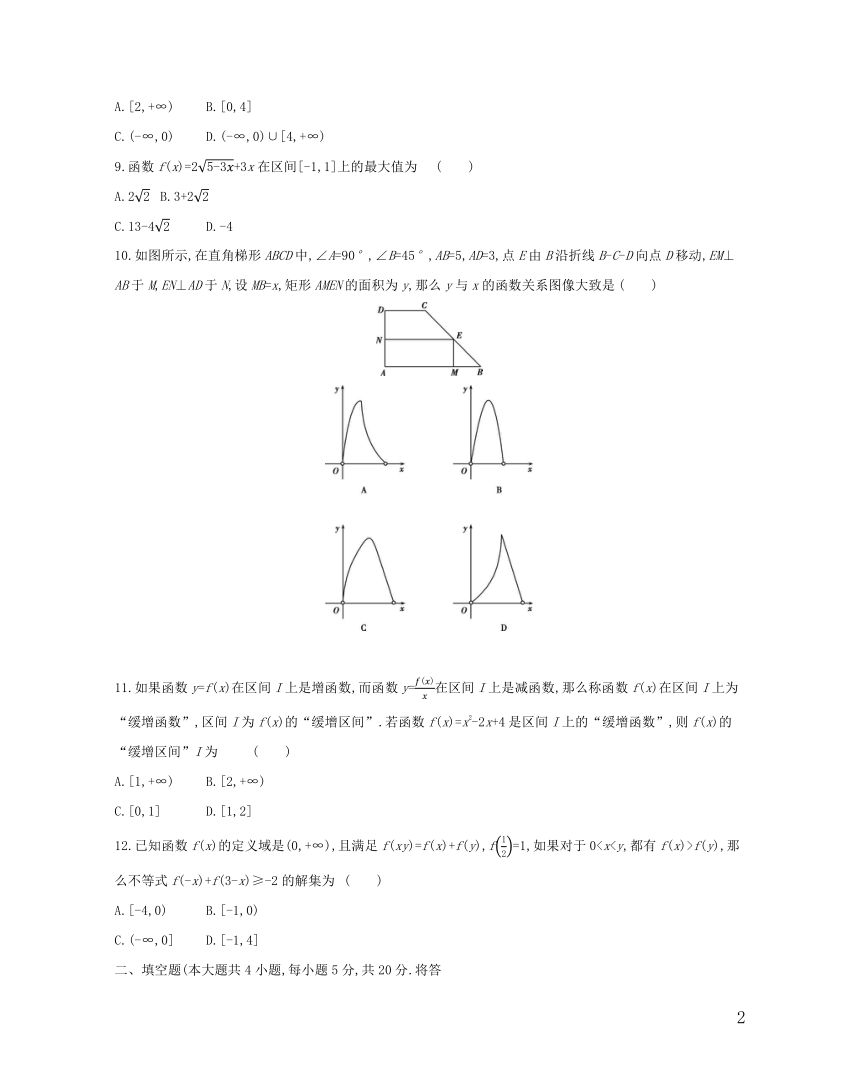
10.如图所示,在直角梯形ABCD中,∠A=90°,∠B=45°,AB=5,AD=3,点E由B沿折线B-C-D向点D移动,EM⊥AB于M,EN⊥AD于N,设MB=x,矩形AMEN的面积为y,那么y与x的函数关系图像大致是 ( )
11.如果函数y=f(x)在区间I上是增函数,而函数y=在区间I上是减函数,那么称函数f(x)在区间I上为“缓增函数”,区间I为f(x)的“缓增区间”.若函数f(x)=x2-2x+4是区间I上的“缓增函数”,则f(x)的“缓增区间”I为 ( )
A.[1,+∞) B.[2,+∞)
C.[0,1] D.[1,2]
12.已知函数f(x)的定义域是(0,+∞),且满足f(xy)=f(x)+f(y),f=1,如果对于0f(y),那么不等式f(-x)+f(3-x)≥-2的解集为 ( )
A.[-4,0) B.[-1,0)
C.(-∞,0] D.[-1,4]
二、填空题(本大题共4小题,每小题5分,共20分.将答
案填在题中横线上)
13.已知f(-1)=x-2,则函数f(x)的解析式为 .
14.已知函数f(x)=|2x-a|的单调递增区间是[3,+∞),则a的值为 .
15.已知函数f(x)=2x2-ax的单调递减区间是(-∞,1],则f(x)在[0,3]上的最大值为 .
16.函数f(x)=[x]的函数值表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2.已知定义在R上的函数g(x)=[x]+[2x],若A={y|y=g(x),0≤x≤1},则A中所有元素的和为 .
三、解答题(本大题共6小题,共70分.解答应写出文字
说明、证明过程或演算步骤)
17.(本小题满分10分)已知幂函数f(x)=(m2-5m+7)·xm-1为偶函数.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-ax-3在[1,3]上不是单调函数,求实数a的取值范围.
18.(本小题满分12分)已知函数y=f(x)是在[-1,1]上的奇函数,当-1≤x<0时,f(x)=-.
(1)判断并证明y=f(x)在[-1,0)上的单调性;
(2)求y=f(x)的值域.
19.(本小题满分12分)已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图像,如图所示.
(1)写出函数f(x)(x∈R)的增区间;
(2)写出函数f(x)(x∈R)的解析式;
(3)若函数g(x)=f(x)-2ax+2(x∈[1,2]),求函数g(x)的最小值.
20.(本小题满分12分)已知函数f(x)=(x∈R).
(1)证明:函数f(x)是偶函数;
(2)记A=f(1)+f(2)+f(3)+…+f(2017),B=f(1)+f+f+…+f,求A+B的值;
(3)若实数x1,x2满足f(x1)+f(x2)>1,求证:|x1x2|>1.
21.(本小题满分12分)已知函数f(x)对任意的实数m,n都有f(m+n)=f(m)+f(n)-1,且当x>0时,有f(x)>1.
(1)求f(0);
(2)求证:f(x)在R上为增函数;
(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.
22.(本小题满分12分)小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元)之间的关系用如图的折线ABC表示,职工每人每月工资为1000元,该店还应交付的其他费用为每月10000元.
(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润 (注:利润=收入-支出).
答案全解全析
第二章 函 数
本章达标检测
1.A 2.A 3.C 4.D 5.B
6.D 7.A 8.B 9.B 10.C
11.D 12.B
一、选择题
1.A 当α=-1时,幂函数y=x-1的定义域为{x|x∈R,且x≠0},不符合题意;当α=时,幂函数y=的定义域为[0,+∞),不符合题意;当α=1时,幂函数y=x的定义域为R且为奇函数,符合题意;当α=2时,幂函数y=x2的定义域为R且为偶函数,不符合题意;当α=3时,幂函数y=x3的定义域为R且为奇函数,符合题意.故选A.
2.A B中,函数非奇非偶;C中,函数是奇函数,均不符合题意;A、D中,函数均为偶函数,A中,函数在(0,+∞)上递增,D中,函数在(0,+∞)上递减,因此A符合题意,故选A.
3.C 解法一:由题可得a-b+8=9a+3b+8,即2a+b=0,所以f(2)=2(2a+b)+8=8.
解法二:由f(-1)=f(3)知,函数图像的对称轴为直线x=1,即-=1,所以2a+b=0,
所以f(2)=2(2a+b)+8=8.
4.D f(-x)=(-x+2)2-mx+1=x2-(4+m)x+5,f(x)=x2+(m+4)x+5.∵函数f(x)=(x+2)2+mx+1是偶函数,∴f(-x)=f(x),即-(4+m)=m+4,解得m=-4.故选D.
5.B 由f=2x-5=4-1,得f(x)=4x-1,又f(a)=6,∴4a-1=6,解得a=.
6.D 依题意得,对于任意x∈R,mx2+mx+1≥0恒成立.
当m=0时,mx2+mx+1=1>0,符合题意;
当m≠0时,由二次函数y=mx2+mx+1的图像没有在x轴下方的点知,
解得0综上所述,0≤m≤4,故选D.
7.A 由函数f(x)是奇函数,且f(1)=-2,可得f(-1)=-f(1)=2,又由函数f(x)在(-∞,+∞)上单调递减,且f(x-1)≤2,即f(x-1)≤f(-1),所以x-1≥-1,解得x≥0,故满足f(x-1)≤2的x的取值区间是[0,+∞).故选A.
8.B 由f(3-x)=f(x+1)可知,f(x)的图像关于直线x=2对称,则f(0)=f(4).
因为当x≥2时,f(x)单调递减,
所以当x<2时,f(x)单调递增,
又f(x)的定义域为R,f(a)≥f(0),
所以a∈[0,4].故选B.
9.B 由题意得y∈[2,8],令=t,所以t∈[,2],x=,所以g(t)=-t2+2t+5(t∈[,2]).因为g(t)在[,2]上单调递减,所以g(t)max=g()=-2+2+5=3+2,所以f(x)在区间[-1,1]上的最大值为3+2,故选B.
10.C ∵EM⊥AB,∠B=45°,
∴EM=MB=x,AM=5-x.
当点E在BC上运动时,
即当0当点E在CD上运动时,矩形AMEN即为矩形AMED,此时3∴y与x的函数关系式为
y=
画出图像如选项C所示.故选C.
11.D 由二次函数的基本性质可知,函数f(x)=x2-2x+4的单调递增区间为[1,+∞).
设g(x)==x+-2,则由对勾函数的性质可知,g(x)在区间(0,2]上为减函数,在区间[2,+∞)上为增函数.因此,f(x)的“缓增区间”I为[1,+∞)∩(0,2]=[1,2].故选D.
12.B 令x=y=1,得f(1)=2f(1),即f(1)=0;令x=,y=2,得f(1)=f(2)+f,即f(2)=-1;令x=y=2,得f(4)=2f(2)=-2.由f(-x)+f(3-x)≥-2,可得f(x2-3x)≥f(4),又因为函数f(x)的定义域是(0,+∞),且对于0f(y),所以即解得-1≤x<0,即不等式f(-x)+f(3-x)≥-2的解集为[-1,0).
二、填空题
13.答案 f(x)=x2-1(x≥-1)
解析 令t=-1,得=t+1,且t≥-1,因此f(t)=(t+1)2-2(t+1)=t2-1(t≥-1).
故函数f(x)的解析式为f(x)=x2-1(x≥-1).
14.答案 6
解析 因为f(x)=|2x-a|=
所以f(x)=|2x-a|的单调递减区间是,单调递增区间是,
又函数f(x)=|2x-a|的单调递增区间是[3,+∞),所以=3,解得a=6.
15.答案 6
解析 因为函数f(x)=2x2-ax的单调递减区间为(-∞,1],所以=1,所以a=4,即f(x)=2x2-4x,所以f(x)在[0,1]上单调递减,在[1,3]上单调递增,又f(0)=0,f(3)=6,所以函数f(x)在[0,3]上的最大值为6.
16.答案 4
解析 当x∈时,0≤2x<1,g(x)=[x]+[2x]=0;当x∈时,1≤2x<2,g(x)=[x]+[2x]=1;
当x=1时,2x=2,g(x)=[x]+[2x]=3.
所以A={y|y=g(x),0≤x≤1}={0,1,3},
所以A中所有元素的和为4.
三、解答题
17.解析 (1)由题意得,m2-5m+7=1,即m2-5m+6=0,解得m=2或m=3, (3分)
又f(x)为偶函数,所以m=3,此时f(x)=x2. (5分)
(2)由(1)知,g(x)=x2-ax-3, (7分)
因为g(x)=f(x)-ax-3在[1,3]上不是单调函数,所以1<<3,解得218.解析 (1)设-1≤x1f(x1)-f(x2)=-=. (3分)
∵-1≤x10,
∴f(x1)-f(x2)<0,即f(x1)∴f(x)在[-1,0)上单调递增. (6分)
(2)∵函数f(x)在[-1,0)上是增函数,
∴f(-1)≤f(x)∴f(x)∈, (8分)
又函数f(x)为奇函数,所以由对称性可知,函数y=f(x)在(0,1]上的取值范围为.(10分)
又f(0)=0,故y=f(x)的值域为∪{0}∪. (12分)
19.解析 (1)根据偶函数的性质及已知条件,将题中f(x)的图像补充完整(图略),由函数图像知f(x)的增区间为[-1,0]和[1,+∞). (3分)
(2)当x>0时,-x<0,f(-x)=(-x)2+2(-x)=x2-2x,又函数f(x)是定义在R上的偶函数,所以f(x)=f(-x)=x2-2x,
所以f(x)= (6分)
(3)由(2)知,g(x)=x2-(2a+2)x+2(x∈[1,2]).因为函数g(x)的图像的对称轴为直线x=-=a+1,
所以①当a+1≤1,即a≤0时,函数g(x)的最小值为g(1)=1-2a;
②当a+1≥2,即a≥1时,函数g(x)的最小值为g(2)=2-4a;
③当1综上所述,g(x)min= (12分)
20.解析 (1)证明:∵x∈R,∴定义域关于原点对称,又f(-x)===f(x),
∴函数f(x)是偶函数. (3分)
(2)当x≠0时,f(x)+f=+=+=1,
∴A+B=[f(1)+f(1)]+f(2)+f
+…+f(2017)+f=2017. (8分)
(3)证明:由f(x1)+f(x2)>1 +>1 (+1)+(+1)>(+1)(+1) >1 |x1x2|>1. (12分)
21.解析 (1)令m=n=0,则f(0)=2f(0)-1,∴f(0)=1. (3分)
(2)证明:任取x1,x2∈R且x1∴x2-x1>0,f(x2-x1)>1.
∵f(m+n)=f(m)+f(n)-1,
∴f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1),
∴f(x2)>f(x1),∴f(x)在R上为增函数. (6分)
(3)∵f(ax-2)+f(x-x2)<3,
即f(ax-2)+f(x-x2)-1<2,
∴f(ax-2+x-x2)<2.
∵f(1)=2,∴f(ax-2+x-x2)又∵f(x)在R上为增函数,
∴ax-2+x-x2<1,
∴x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立. (8分)
令g(x)=x2-(a+1)x+3(x≥1),
只需满足g(x)min>0即可.
当≤1,即a≤1时,g(x)在[1,+∞)上递增,
因此g(x)min=g(1),
由g(1)>0得a<3,此时a≤1; (10分)
当>1,即a>1时,g(x)min=g,
由g>0得-2-1此时1综上,实数a的取值范围为(-∞,2-1). (12分)
22.解析 (1)当40≤x≤60时,设AB的方程为y=k1x+b1,将A,B两点坐标代入方程得解得所以AB的方程为y=-2x+140;
当60≤x≤80时,同理可得BC的方程为y=-x+50,
所以y= (4分)
(2)设该店有职工m名,当x=50时,
该店总收入为100(-2×50+140)(50-40)=40000(元),
又该店的总支出为(1000m+10000)元,
所以依题意得40000=1000m+10000,
解得m=30.
所以此时该店有30名职工. (6分)
(3)设月利润为S元,若该店只有20名职工,则月利润
S= (8分)
当40≤x≤60时,S=-200(x-55)2+15000,
所以当x=55时,S取最大值,为15000;
当60所以当x=70时,S取最大值,为15000. (10分)
故当x=55或x=70时,S取最大值15000元,即销售单价定为55元或70元时,该专卖店月利润最大. (12分)
11
本章达标检测
(满分:150分;时间:120分钟)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设α∈-1,,1,2,3,使函数y=xα的定义域为R且为奇函数的所有α的值为 ( )
A.1,3 B.1,2
C.2,3 D.-1,1,3
2.下列函数中,既是偶函数又在区间(0,+∞)上是增函数的是 ( )
A.y=|x| B.y=3-x
C.y= D.y=-x2+4
3.二次函数f(x)=ax2+bx+8满足条件f(-1)=f(3),则f(2)的值为 ( )
A.5 B.6
C.8 D.与a,b值有关
4.函数f(x)=(x+2)2+mx+1是偶函数,则m= ( )
A.0 B.2
C.4 D.-4
5.已知f=2x-5,且f(a)=6,则a等于 ( )
A.- B.
C. D.-
6.已知函数f(x)=的定义域是一切实数,则m的取值范围是 ( )
A.0
7.已知奇函数f(x)在(-∞,+∞)上单调递减,若f(1)=-2,则满足f(x-1)≤2的x的取值区间是 ( )
A.[0,+∞) B.(-∞,0]
C.[2,+∞) D.(-∞,2]
8.已知定义域为R的函数f(x)满足f(3-x)=f(x+1),当x≥2时,f(x)单调递减,且f(a)≥f(0),则实数a的取值范围是( )
A.[2,+∞) B.[0,4]
C.(-∞,0) D.(-∞,0)∪[4,+∞)
9.函数f(x)=2+3x在区间[-1,1]上的最大值为 ( )
A.2 B.3+2
C.13-4 D.-4
10.如图所示,在直角梯形ABCD中,∠A=90°,∠B=45°,AB=5,AD=3,点E由B沿折线B-C-D向点D移动,EM⊥AB于M,EN⊥AD于N,设MB=x,矩形AMEN的面积为y,那么y与x的函数关系图像大致是 ( )
11.如果函数y=f(x)在区间I上是增函数,而函数y=在区间I上是减函数,那么称函数f(x)在区间I上为“缓增函数”,区间I为f(x)的“缓增区间”.若函数f(x)=x2-2x+4是区间I上的“缓增函数”,则f(x)的“缓增区间”I为 ( )
A.[1,+∞) B.[2,+∞)
C.[0,1] D.[1,2]
12.已知函数f(x)的定义域是(0,+∞),且满足f(xy)=f(x)+f(y),f=1,如果对于0
A.[-4,0) B.[-1,0)
C.(-∞,0] D.[-1,4]
二、填空题(本大题共4小题,每小题5分,共20分.将答
案填在题中横线上)
13.已知f(-1)=x-2,则函数f(x)的解析式为 .
14.已知函数f(x)=|2x-a|的单调递增区间是[3,+∞),则a的值为 .
15.已知函数f(x)=2x2-ax的单调递减区间是(-∞,1],则f(x)在[0,3]上的最大值为 .
16.函数f(x)=[x]的函数值表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2.已知定义在R上的函数g(x)=[x]+[2x],若A={y|y=g(x),0≤x≤1},则A中所有元素的和为 .
三、解答题(本大题共6小题,共70分.解答应写出文字
说明、证明过程或演算步骤)
17.(本小题满分10分)已知幂函数f(x)=(m2-5m+7)·xm-1为偶函数.
(1)求f(x)的解析式;
(2)若g(x)=f(x)-ax-3在[1,3]上不是单调函数,求实数a的取值范围.
18.(本小题满分12分)已知函数y=f(x)是在[-1,1]上的奇函数,当-1≤x<0时,f(x)=-.
(1)判断并证明y=f(x)在[-1,0)上的单调性;
(2)求y=f(x)的值域.
19.(本小题满分12分)已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图像,如图所示.
(1)写出函数f(x)(x∈R)的增区间;
(2)写出函数f(x)(x∈R)的解析式;
(3)若函数g(x)=f(x)-2ax+2(x∈[1,2]),求函数g(x)的最小值.
20.(本小题满分12分)已知函数f(x)=(x∈R).
(1)证明:函数f(x)是偶函数;
(2)记A=f(1)+f(2)+f(3)+…+f(2017),B=f(1)+f+f+…+f,求A+B的值;
(3)若实数x1,x2满足f(x1)+f(x2)>1,求证:|x1x2|>1.
21.(本小题满分12分)已知函数f(x)对任意的实数m,n都有f(m+n)=f(m)+f(n)-1,且当x>0时,有f(x)>1.
(1)求f(0);
(2)求证:f(x)在R上为增函数;
(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.
22.(本小题满分12分)小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元)之间的关系用如图的折线ABC表示,职工每人每月工资为1000元,该店还应交付的其他费用为每月10000元.
(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润 (注:利润=收入-支出).
答案全解全析
第二章 函 数
本章达标检测
1.A 2.A 3.C 4.D 5.B
6.D 7.A 8.B 9.B 10.C
11.D 12.B
一、选择题
1.A 当α=-1时,幂函数y=x-1的定义域为{x|x∈R,且x≠0},不符合题意;当α=时,幂函数y=的定义域为[0,+∞),不符合题意;当α=1时,幂函数y=x的定义域为R且为奇函数,符合题意;当α=2时,幂函数y=x2的定义域为R且为偶函数,不符合题意;当α=3时,幂函数y=x3的定义域为R且为奇函数,符合题意.故选A.
2.A B中,函数非奇非偶;C中,函数是奇函数,均不符合题意;A、D中,函数均为偶函数,A中,函数在(0,+∞)上递增,D中,函数在(0,+∞)上递减,因此A符合题意,故选A.
3.C 解法一:由题可得a-b+8=9a+3b+8,即2a+b=0,所以f(2)=2(2a+b)+8=8.
解法二:由f(-1)=f(3)知,函数图像的对称轴为直线x=1,即-=1,所以2a+b=0,
所以f(2)=2(2a+b)+8=8.
4.D f(-x)=(-x+2)2-mx+1=x2-(4+m)x+5,f(x)=x2+(m+4)x+5.∵函数f(x)=(x+2)2+mx+1是偶函数,∴f(-x)=f(x),即-(4+m)=m+4,解得m=-4.故选D.
5.B 由f=2x-5=4-1,得f(x)=4x-1,又f(a)=6,∴4a-1=6,解得a=.
6.D 依题意得,对于任意x∈R,mx2+mx+1≥0恒成立.
当m=0时,mx2+mx+1=1>0,符合题意;
当m≠0时,由二次函数y=mx2+mx+1的图像没有在x轴下方的点知,
解得0
7.A 由函数f(x)是奇函数,且f(1)=-2,可得f(-1)=-f(1)=2,又由函数f(x)在(-∞,+∞)上单调递减,且f(x-1)≤2,即f(x-1)≤f(-1),所以x-1≥-1,解得x≥0,故满足f(x-1)≤2的x的取值区间是[0,+∞).故选A.
8.B 由f(3-x)=f(x+1)可知,f(x)的图像关于直线x=2对称,则f(0)=f(4).
因为当x≥2时,f(x)单调递减,
所以当x<2时,f(x)单调递增,
又f(x)的定义域为R,f(a)≥f(0),
所以a∈[0,4].故选B.
9.B 由题意得y∈[2,8],令=t,所以t∈[,2],x=,所以g(t)=-t2+2t+5(t∈[,2]).因为g(t)在[,2]上单调递减,所以g(t)max=g()=-2+2+5=3+2,所以f(x)在区间[-1,1]上的最大值为3+2,故选B.
10.C ∵EM⊥AB,∠B=45°,
∴EM=MB=x,AM=5-x.
当点E在BC上运动时,
即当0
y=
画出图像如选项C所示.故选C.
11.D 由二次函数的基本性质可知,函数f(x)=x2-2x+4的单调递增区间为[1,+∞).
设g(x)==x+-2,则由对勾函数的性质可知,g(x)在区间(0,2]上为减函数,在区间[2,+∞)上为增函数.因此,f(x)的“缓增区间”I为[1,+∞)∩(0,2]=[1,2].故选D.
12.B 令x=y=1,得f(1)=2f(1),即f(1)=0;令x=,y=2,得f(1)=f(2)+f,即f(2)=-1;令x=y=2,得f(4)=2f(2)=-2.由f(-x)+f(3-x)≥-2,可得f(x2-3x)≥f(4),又因为函数f(x)的定义域是(0,+∞),且对于0
二、填空题
13.答案 f(x)=x2-1(x≥-1)
解析 令t=-1,得=t+1,且t≥-1,因此f(t)=(t+1)2-2(t+1)=t2-1(t≥-1).
故函数f(x)的解析式为f(x)=x2-1(x≥-1).
14.答案 6
解析 因为f(x)=|2x-a|=
所以f(x)=|2x-a|的单调递减区间是,单调递增区间是,
又函数f(x)=|2x-a|的单调递增区间是[3,+∞),所以=3,解得a=6.
15.答案 6
解析 因为函数f(x)=2x2-ax的单调递减区间为(-∞,1],所以=1,所以a=4,即f(x)=2x2-4x,所以f(x)在[0,1]上单调递减,在[1,3]上单调递增,又f(0)=0,f(3)=6,所以函数f(x)在[0,3]上的最大值为6.
16.答案 4
解析 当x∈时,0≤2x<1,g(x)=[x]+[2x]=0;当x∈时,1≤2x<2,g(x)=[x]+[2x]=1;
当x=1时,2x=2,g(x)=[x]+[2x]=3.
所以A={y|y=g(x),0≤x≤1}={0,1,3},
所以A中所有元素的和为4.
三、解答题
17.解析 (1)由题意得,m2-5m+7=1,即m2-5m+6=0,解得m=2或m=3, (3分)
又f(x)为偶函数,所以m=3,此时f(x)=x2. (5分)
(2)由(1)知,g(x)=x2-ax-3, (7分)
因为g(x)=f(x)-ax-3在[1,3]上不是单调函数,所以1<<3,解得2
∵-1≤x1
∴f(x1)-f(x2)<0,即f(x1)
(2)∵函数f(x)在[-1,0)上是增函数,
∴f(-1)≤f(x)
又函数f(x)为奇函数,所以由对称性可知,函数y=f(x)在(0,1]上的取值范围为.(10分)
又f(0)=0,故y=f(x)的值域为∪{0}∪. (12分)
19.解析 (1)根据偶函数的性质及已知条件,将题中f(x)的图像补充完整(图略),由函数图像知f(x)的增区间为[-1,0]和[1,+∞). (3分)
(2)当x>0时,-x<0,f(-x)=(-x)2+2(-x)=x2-2x,又函数f(x)是定义在R上的偶函数,所以f(x)=f(-x)=x2-2x,
所以f(x)= (6分)
(3)由(2)知,g(x)=x2-(2a+2)x+2(x∈[1,2]).因为函数g(x)的图像的对称轴为直线x=-=a+1,
所以①当a+1≤1,即a≤0时,函数g(x)的最小值为g(1)=1-2a;
②当a+1≥2,即a≥1时,函数g(x)的最小值为g(2)=2-4a;
③当1
20.解析 (1)证明:∵x∈R,∴定义域关于原点对称,又f(-x)===f(x),
∴函数f(x)是偶函数. (3分)
(2)当x≠0时,f(x)+f=+=+=1,
∴A+B=[f(1)+f(1)]+f(2)+f
+…+f(2017)+f=2017. (8分)
(3)证明:由f(x1)+f(x2)>1 +>1 (+1)+(+1)>(+1)(+1) >1 |x1x2|>1. (12分)
21.解析 (1)令m=n=0,则f(0)=2f(0)-1,∴f(0)=1. (3分)
(2)证明:任取x1,x2∈R且x1
∵f(m+n)=f(m)+f(n)-1,
∴f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1),
∴f(x2)>f(x1),∴f(x)在R上为增函数. (6分)
(3)∵f(ax-2)+f(x-x2)<3,
即f(ax-2)+f(x-x2)-1<2,
∴f(ax-2+x-x2)<2.
∵f(1)=2,∴f(ax-2+x-x2)
∴ax-2+x-x2<1,
∴x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立. (8分)
令g(x)=x2-(a+1)x+3(x≥1),
只需满足g(x)min>0即可.
当≤1,即a≤1时,g(x)在[1,+∞)上递增,
因此g(x)min=g(1),
由g(1)>0得a<3,此时a≤1; (10分)
当>1,即a>1时,g(x)min=g,
由g>0得-2-1
22.解析 (1)当40≤x≤60时,设AB的方程为y=k1x+b1,将A,B两点坐标代入方程得解得所以AB的方程为y=-2x+140;
当60≤x≤80时,同理可得BC的方程为y=-x+50,
所以y= (4分)
(2)设该店有职工m名,当x=50时,
该店总收入为100(-2×50+140)(50-40)=40000(元),
又该店的总支出为(1000m+10000)元,
所以依题意得40000=1000m+10000,
解得m=30.
所以此时该店有30名职工. (6分)
(3)设月利润为S元,若该店只有20名职工,则月利润
S= (8分)
当40≤x≤60时,S=-200(x-55)2+15000,
所以当x=55时,S取最大值,为15000;
当60
故当x=55或x=70时,S取最大值15000元,即销售单价定为55元或70元时,该专卖店月利润最大. (12分)
11
