河南省顶尖名校2021-2022学年高二上学期第二次素养调研(1月)理科数学试题(PDF版含答案)
文档属性
| 名称 | 河南省顶尖名校2021-2022学年高二上学期第二次素养调研(1月)理科数学试题(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 661.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-15 12:48:09 | ||
图片预览



文档简介
河南省顶尖名校 2021-2022 学年高二上学期第二次素养调研
理科数学试卷
考生注意:
1.本试卷满分 150 分,考试时间 120 分钟。
2.答题前,考生务必用直径 0.5 毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用 2B 铅笔把答题卡上
对应题目的答案标号涂黑;非选择题请用直径 0.5 毫米黑色墨水签字笔在答题卡上各题的
答题区域内作答,超.出.答.题.区.域.书.写.的.答.案.无.效.,.在.试.题.卷.、.草.稿.纸.上.作.答.无.效.。
一、选择题(本大题共 12 小题,每小题 5 分,满分 60 分. 在每小题给出的四个选项中,只
有一项是符合题目要求的。)
1. 与向量(-3,-4,5)共线的单位向量是 ( )
(A) (3 2 , 2 2 , 2 ) ( 3 2 , 2 2 , 2 ) (B) (3 2 , 2 2 2. 和 . , )
10 5 2 10 5 2 10 5 2
(C) (3 2. , 2 2 , 2 ) 和 ( 3 2 , 2 2 , 2 ) (D) 3 2 2 2 2. ( , , )
10 5 2 10 5 2 10 5 2
x2 y2
2.已知点 (3, 2) 在椭圆 2 2 1上,则 ( )a b
(A) .点 ( 3, 2) 不在椭圆上 (B) . 点 (3, 2) 不在椭圆上
(C) .点 ( 3,2)在椭圆上 (D) .无法判断点 ( 3, 2) 、 (3, 2) 、 ( 3,2)是否在椭圆上
3.平行六面体 ABCD A1B1C1D1 中, AC1 xAB 2yBC 3zC1C ,
则 x y z ( )
(A) .1 (B) 7. (C) . 5 (D) .2
6 6 3
4.已知向量a (0,0,1),b (0,1,1), 则a与b的夹角为 ( )
(A) .0° (B).45° (C).90° (D).180°
5.已知六棱锥 P-ABCDEF 的底面是正六边形,PA⊥平面 ABC,PA=2AB,则下列结论正确的个
数是 ( )
①PA⊥AD
②平面 ABC⊥平面 PBC
③直线 BC∥平面 PAE
④直线 PD与平面 ABC 所成角为30
(A).1 个 (B) .2 个 (C) .3 个 (D) .4 个
6.如图是抛物线形拱桥,当水面在图中位置时,拱顶离水面 2 米,水面宽 4 米.水下降 1 米后,
水面宽为 ( )
(A) . 3 米 (B) . 2 3 米
(C) . 6 米 (D) . 2 6 米
7.给出下列命题:
①直线 l的方向向量为a=(1,-1,2) 1,直线m的方向向量为b=(2,1,- )则 l m
2
②直线 l的方向向量为a=(0,1,-1),平面 的法向量为n=(1,-1,-1), l 则 l .
③平面 , 的法向量分别为n1=(0,1,3),n2=(1,0,2),则 // .
④平面 经过三点 A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面 的法向量,
则 u+t=1.
其中真命题的序号是 ( )
(A) .②③ (B) .①④ (C) .③④ (D) .①②
x2 16y2
8.若双曲线 2 1的左焦点在抛物线 y
2 2px的准线上,则 p的值为 ( )
3 p
A. 2 B. 3 C. 4 D. 4 2
9.如图,正方体 ABCD A1B1C1D1 的棱长为 1,O 是底面
A1B1C1D1的中心,则点 O 到平面 ABC1D1的距离为( )
(A) .1 (B) . 2 (C) . 2 (D) . 3
2 4 2 2
x2 y2
10.若双曲线 2 2 1 ( a 0,b 0 )的右支上到原点和右焦点距离相等的点有两个, 则a b
双曲线离心率的取值范围是 ( )
(A) . e 2 (B) . 1 e 2 (C) . e 2 (D) .1 e 2
11. C y 2 4x y 2对于抛物线 : ,我们称满足 0 4x0 的点M (x0 , y0 )在抛物线的内部.若点
M (x0 , y0 )在抛物线内部,则直线 l : y0 y 2(x x0 ) 与曲线 C ( )
(A) . 恰有一个公共点 (B) . 恰有 2 个公共点
(C) . 可能有一个公共点,也可能有两个公共点 (D) . 没有公共点
x2 y2
12.已知 F1 、F2 是椭圆 2 2 1( a b 0 )的两个焦点, P是椭圆上任意一点,从任一焦a b
点引 F1PF2 的外角平分线的垂线,垂足为Q , 则点Q的轨迹 ( )
(A) . 圆 (B) . 椭圆 (C) . 双曲线 (D) . 抛物线
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.已知命题 p: x∈R,x2+x+1>0,则 p 为 。
14.2021 年 2 月某地发生新冠肺炎疫情,急需从一所三甲医院的呼吸科抽调部分医生参加救
援,该呼吸科共有男女医生各 10 人,要求抽调的女医生至少有 1 人,男医生至少比女医生
多 2 人,为了保证该院呼吸科的正常运转,从该院呼吸科抽调的医生人数不能超过 10 人。
已知每名男医生一天可以给 40 名病人进行康复治疗,每名女医生一天可以给 35 名病人进行
康复治疗,那么应该从该呼吸科抽调男医生 人,女医生 人,从而使
每天获得康复治疗的病人最多。
15.在等比数列{an}中,a5-a3=12,a6-a4=24,记数列{an}的前 n 项和、前 n 项积分别为 Sn,
Sn 1
2
Tn,则 n= 时, 的值最大。
Tn
B C
16.在△ABC 中,角 A,B,C 所对应的边分别为 a,b,c, 3 bsin =asinB,△ABC 的
2
外接圆面积为 12π,则△ABC 面积的最大值是 。
三、解答题(本大题共 6个小题,共 70分)
17.(本题 10 分)如图所示,在空间四边形 ABCD中, E, F分别为 AB, AD的中点,G,
H 分别在BC,CD上,且BG :GC DH :HC 1: 2.求证:(1)E、F、G、H 四点共面;
(2) EG与HF的交点在直线 AC上.
18.在四棱锥 P﹣ABCD 中,∠ABC=∠ACD=90°,∠
BAC=∠CAD=60°,PA⊥平面 ABCD,E 为 PD 的中点,PA=2AB=2.求:
(1)求四棱锥 P﹣ABCD 的体积 V;
(2)若 F 为 PC 的中点,求证 PC⊥平面 AEF.
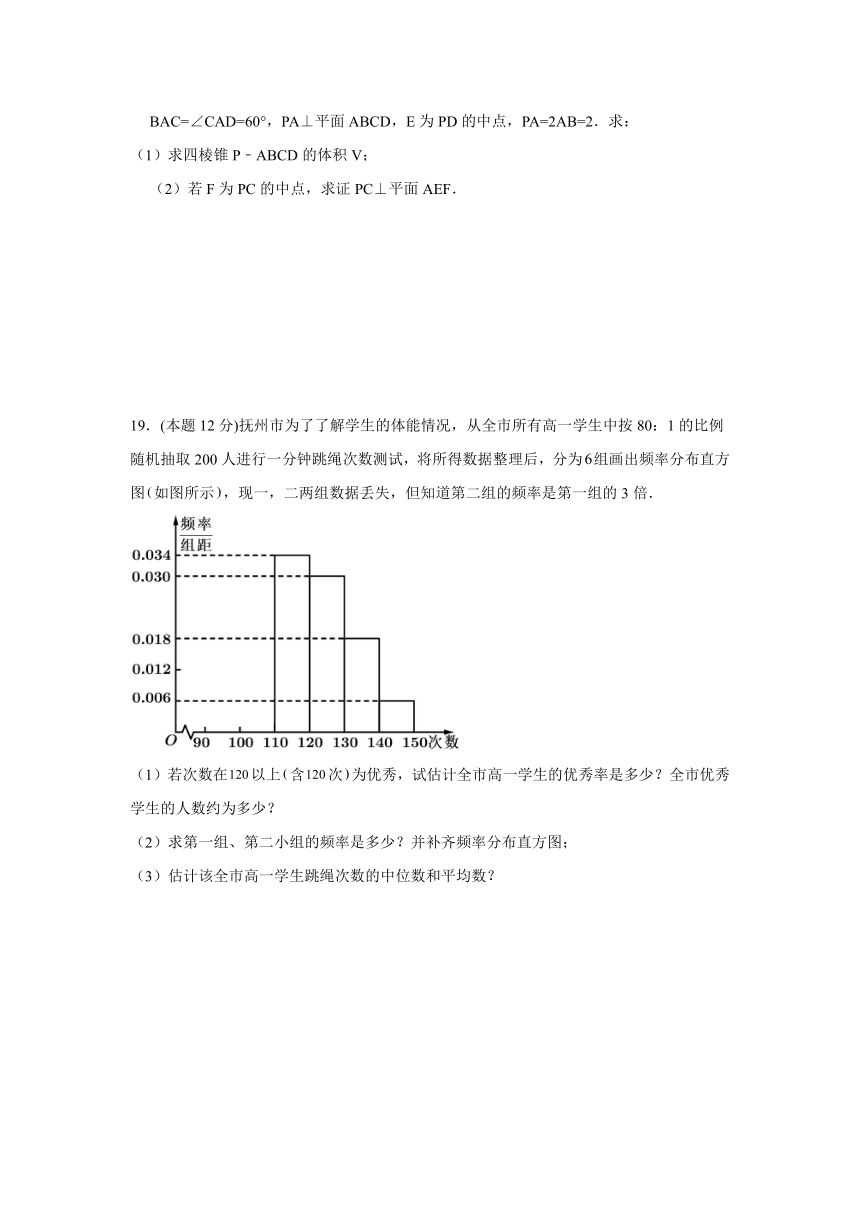
19.(本题 12 分)抚州市为了了解学生的体能情况,从全市所有高一学生中按 80:1 的比例
随机抽取 200 人进行一分钟跳绳次数测试,将所得数据整理后,分为6组画出频率分布直方
图 (如图所示 ),现一,二两组数据丢失,但知道第二组的频率是第一组的 3 倍.
(1)若次数在120以上 (含120次 )为优秀,试估计全市高一学生的优秀率是多少?全市优秀
学生的人数约为多少?
(2)求第一组、第二小组的频率是多少?并补齐频率分布直方图;
(3)估计该全市高一学生跳绳次数的中位数和平均数?
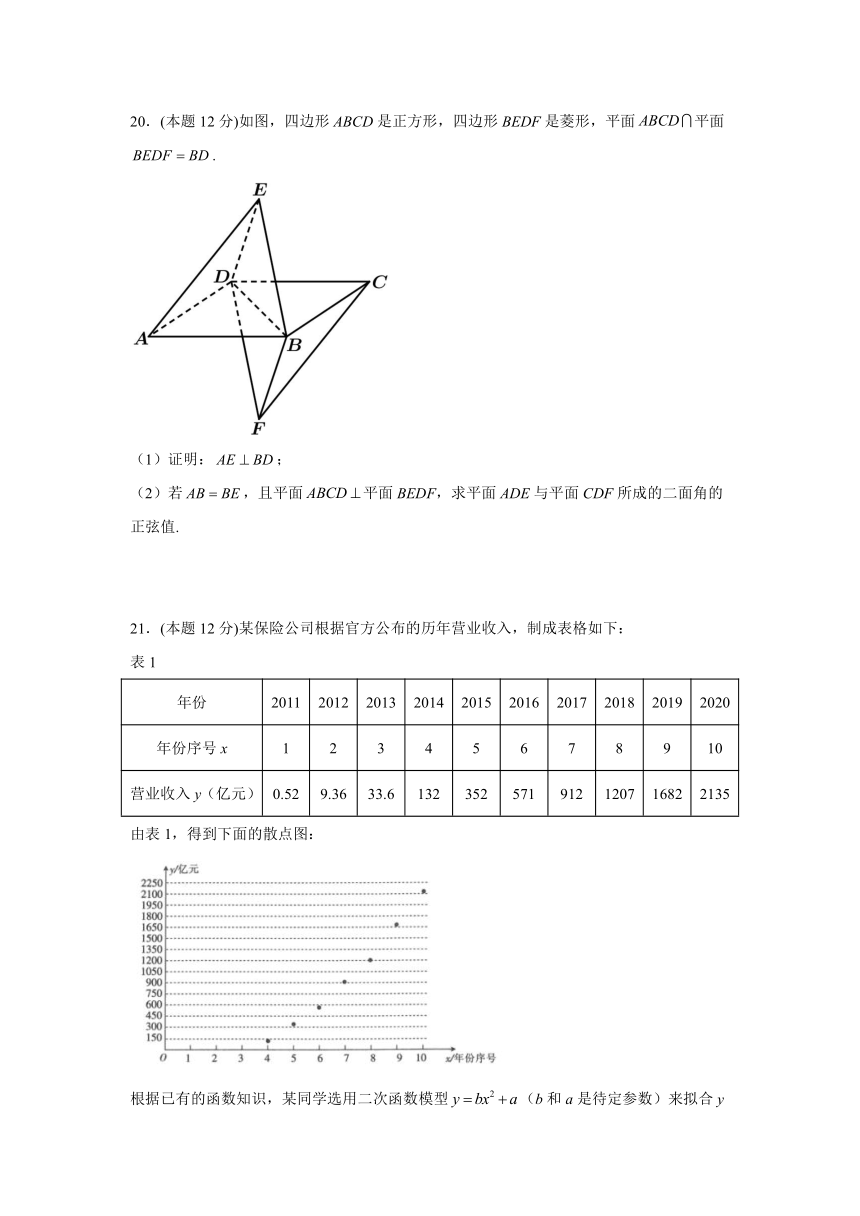
20.(本题 12 分)如图,四边形 ABCD是正方形,四边形 BEDF是菱形,平面 ABCD 平面
BEDF BD .
(1)证明: AE BD;
(2)若 AB BE,且平面 ABCD 平面 BEDF,求平面 ADE与平面 CDF所成的二面角的
正弦值.
21.(本题 12 分)某保险公司根据官方公布的历年营业收入,制成表格如下:
表 1
年份 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020
年份序号 x 1 2 3 4 5 6 7 8 9 10
营业收入 y(亿元) 0.52 9.36 33.6 132 352 571 912 1207 1682 2135
由表 1,得到下面的散点图:
根据已有的函数知识,某同学选用二次函数模型 y bx2 a(b和 a是待定参数)来拟合 y
和 x的关系.这时,可以对年份序号做变换,即令 t x2 ,得 y bt a,由表 1 可得变换后的
数据见表 2.
表 2
t 1 4 9 16 25 36 49 64 81 100
y 0.52 9.36 33.6 132 352 571 912 1207 1682 2135
(1)根据表中数据,建立 y关于 t的回归方程(系数精确到个位数);
(2)根据(1)中得到的回归方程估计 2021 年的营业收入,以及营业收入首次超过 4000
亿元的年份.
附:对于一组数据 u1,v1 , u2 ,v2 , , un ,vn ,其回归直线 v u 的斜率和截距的最小二
n
ui u vi v
乘估计分别为 i 1 n , v u .
2 ui u
i 1
10 2 10
参考数据: t 38.5, y 703.45, t i t 1.051 10 4, t i t y i y 2.327 10 5 .
i 1 i 1
22.(本题 12 分)如图,在三棱柱 ABC A1B1C1中, BB1 平面 ABC, AB BC,
AA1 AB BC 2 .
(1)求证:BC1 平面 A1B1C;
B M 1
(2)点 M BC 1在线段 1 上,且 B C 3 ,试问在线段 A1B上是否存在一点 N,满足MN // 平面1
AN
A1ACC
1
1 ,若存在求 AB 的值,若不存在,请说明理由?1
理科数学答案
题号 1 3 4 5 6 7 8 9 10 11 12
答案 A B B A D B C B C D A
17.(1)证明见解析;(2)证明见解析.
证明(1)∵BG :GC DH :HC,∴GH //BD. --------1 分
∵ E, F分别为 AB, AD的中点, --------3 分
∴ EF //BD,∴ EF //GH ,∴ E, F,G,H四点共面. --------5 分
(2)∵G,H不是 BC,CD的中点,
∴ EF //GH ,且 EF GH ,故 EFHG为梯形.
∴ EG与 FH 必相交,设交点为M , -------6 分
∴ EG 平面 ABC,FH 平面 ACD,
∴M 平面 ABC,且M 平面 ACD, -------8 分
∴M AC,即GE与HF的交点在直线 AC上. -------10 分
18 5 3.(1) ,(2)见解析.
3
试题解析:
(1)在 Rt ABC中, AB 1, BAC 60 , BC 3, AC 2 .
在 Rt ACD中 AC 2, CAD 60 , ---------2 分
CD 2 3, AD 4, S 1 1ABCD AB·BC AC·CD --------4 分2 2
1 1 5
1 3 2 2 3 3 .
2 2 2
V 1 5 3 2 5则 3 . ---------6 分
3 2 3
(2) PA CA, F为 PC的中点, AF PC .
PA 平面 ABCD, PA CD . ---------8 分
AC CD,PA AC A, CD 平面 PAC, CD PC .
E为 PD中点,F 为 PC为中点, EF CD,则 EF PC . --------10 分
AF EF F , PC 平面 AEF . --------12 分
考点:四棱锥的体积公式;直线与平面垂直的判定与证明.
19.(1)8640;(2)第一组频率为0.03,第二组频率为0.09 .频率分布直方图见解析;(3)
334
中位数为 ,均值为 121.9
3
(1)由频率分布直方图,分数在 120 分以上的频率为 (0.030 0.018 0.006) 10 0.54,
因此优秀学生有0.54 200 80 8640(人); -------4 分
(2)设第一组频率为 x,则第二组频率为3x,
所以 x 3x 0.34 0.54 1, x 0.03,
第一组频率为0.03,第二组频率为0.09 . -------6 分
频率分布直方图如下: -------8 分
(3)前 3 组数据的频率和为 (0.003 0.009 0.034) 10 0.46,中位数在第四组,
n n 110设中位数为 ,则 0.3 0.46 0.5, n 334 . ------10 分
120 110 3
均值为0.03 95 0.09 105 0.34 115 0.3 125 0.18 135 0.06 145 121.9.------12 分
20 1 2 2 2.( )证明见解析;( ) .
3
(1)证明:如图,连接 AC交 BD于点O,连接OE.
四边形 ABCD为正方形,
BD OA,且O为BD的中点.
又 四边形BEDF为菱形,
BD OE. -------2 分
∵OA OE O,OA,OE 平面OAE,
BD 平面OAE, -------4 分
又 AE 平面 OAE
BD AE. --------6 分
(2)解:如图,建立空间直角坐标系,不妨设 AB 2 ,
则 BD 2 2 ,OE 2 ,
则 A(2,0,0),D(0,0,0),C(0, 2,0).
由(1)得OE BD,
又 平面 ABCD 平面 BEDF,平面 ABCD 平面 BEDF BD,
OE 平面 ABCD,故 E(1,1, 2),同理F (1,1, 2) ,
DA (2,0,0),DE (1,1, 2),DC (0, 2,0),DF (1,1, 2). ------8 分
m (x 设 1, y1, z1)为平面DAE的法向量, n (x2 , y2 , z2 )为平面DCF的法向量,
m ·DA 2x1 0,
则 故可取m (0, 2,1),
m·DE x1 y1 2z1 0,
n ·DC 2y2 0,
同理 故可取 n ( 2,0,1), -------10 分
n·DF x2 y2 2z2 0,
m ·n 1 1
所以 cos m,n m n 3 3 3 .
2
设平面 ADE与平面CDF所成的二面角为 1 2 2,则 sin 1 ,
3 3
所以平面 ADE与平面CDF 2 2所成的二面角的正弦值为 . -------12 分
3
21.(1) y 22t 144 ;(2)估计 2021 年的营业收入约为 2518 亿元,估计营业收入首次超
过 4000 亿元的年份为 2024 年.
10
ti t yi y
b i 1 2.327 10
5
(1) 10 22, --------3 分
t t 2 1.051 10
4
i
i 1
a y b t 703.45 22 38.5 144 , --------5 分
故回归方程为 y 22t 144 . --------6 分
(2)2021 年对应的 t的值为 121,营业收入 y 22 121 144 2518,
所以估计 2021 年的营业收入约为 2518 亿元. -------8 分
依题意有 22t 144 4000,解得 t 188.4,故 x2 188.4 .
因为13 188.4 14, -------10 分
所以估计营业收入首次超过 4000 亿元的年份序号为 14,即 2024 年.--------12 分
AN 2
22.(1 1)证明见解析;(2)存在, AB 的值为 .1 3
(1)在三棱柱 ABC A1B1C1中, BB1 平面 ABC, AB BC, AA1 AB BC 2 .
∴ BC1 B1C,BB1 A1B1, A1B1 B1C1,
∵ BB1 B1C1 B1 , ------2 分
∴ A1B1 平面 BBC1B1,
∵BC1 平面 BBC1B1,
∴ A1B1 BC1, -------4 分
∵ A1B1 B1C B1 ,
∴BC1 平面 A1B1C . -------5 分
(2)以 B为原点, BC为 x轴, BA为 y轴, BB1 为轴,建立空间直角坐标系,如图,
A 0,2,0 C 2,0,0 C1 2,0, 2 , B 0,0,0 , B1 0,0,2 , A1 0, 2, 2 ,
所以CA 2, 2,0 ,CC 0,0, 2 , --------7 分1
n C A 2x 2y 0设平面 ACC1A1 的法向量 n x, y, z ,则 n
,
CC1 2z 0
取 x 1,得 n 1,1,0 , --------8 分
B M 1
点 M BC 1在线段 1 上,且 A BB C 3 ,点 N在线段 1 上,设M a,b,c , N x, y, z ,1
A1N 设 A B ,则 B1C 3B M,1 A N A B, 0≤ ≤1,1 11
即 2,0, 2 3 a,b,c 2 , x, y 2, z 2 0, 2, 2
M 2 ,0, 4 解得 , N 0,2 2 , 2 2 3 3 ,
MN 2 , 2 2 ,
2
2 , -------10 分
3 3
∵MN //平面A1ACC1,
2 AN
∴ n MN 2 2 0
2 1 2
,解得 .∴ 的值为 . --------12 分
3 3 A1B 3
理科数学试卷
考生注意:
1.本试卷满分 150 分,考试时间 120 分钟。
2.答题前,考生务必用直径 0.5 毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用 2B 铅笔把答题卡上
对应题目的答案标号涂黑;非选择题请用直径 0.5 毫米黑色墨水签字笔在答题卡上各题的
答题区域内作答,超.出.答.题.区.域.书.写.的.答.案.无.效.,.在.试.题.卷.、.草.稿.纸.上.作.答.无.效.。
一、选择题(本大题共 12 小题,每小题 5 分,满分 60 分. 在每小题给出的四个选项中,只
有一项是符合题目要求的。)
1. 与向量(-3,-4,5)共线的单位向量是 ( )
(A) (3 2 , 2 2 , 2 ) ( 3 2 , 2 2 , 2 ) (B) (3 2 , 2 2 2. 和 . , )
10 5 2 10 5 2 10 5 2
(C) (3 2. , 2 2 , 2 ) 和 ( 3 2 , 2 2 , 2 ) (D) 3 2 2 2 2. ( , , )
10 5 2 10 5 2 10 5 2
x2 y2
2.已知点 (3, 2) 在椭圆 2 2 1上,则 ( )a b
(A) .点 ( 3, 2) 不在椭圆上 (B) . 点 (3, 2) 不在椭圆上
(C) .点 ( 3,2)在椭圆上 (D) .无法判断点 ( 3, 2) 、 (3, 2) 、 ( 3,2)是否在椭圆上
3.平行六面体 ABCD A1B1C1D1 中, AC1 xAB 2yBC 3zC1C ,
则 x y z ( )
(A) .1 (B) 7. (C) . 5 (D) .2
6 6 3
4.已知向量a (0,0,1),b (0,1,1), 则a与b的夹角为 ( )
(A) .0° (B).45° (C).90° (D).180°
5.已知六棱锥 P-ABCDEF 的底面是正六边形,PA⊥平面 ABC,PA=2AB,则下列结论正确的个
数是 ( )
①PA⊥AD
②平面 ABC⊥平面 PBC
③直线 BC∥平面 PAE
④直线 PD与平面 ABC 所成角为30
(A).1 个 (B) .2 个 (C) .3 个 (D) .4 个
6.如图是抛物线形拱桥,当水面在图中位置时,拱顶离水面 2 米,水面宽 4 米.水下降 1 米后,
水面宽为 ( )
(A) . 3 米 (B) . 2 3 米
(C) . 6 米 (D) . 2 6 米
7.给出下列命题:
①直线 l的方向向量为a=(1,-1,2) 1,直线m的方向向量为b=(2,1,- )则 l m
2
②直线 l的方向向量为a=(0,1,-1),平面 的法向量为n=(1,-1,-1), l 则 l .
③平面 , 的法向量分别为n1=(0,1,3),n2=(1,0,2),则 // .
④平面 经过三点 A(1,0,-1),B(0,1,0),C(-1,2,0),向量n=(1,u,t)是平面 的法向量,
则 u+t=1.
其中真命题的序号是 ( )
(A) .②③ (B) .①④ (C) .③④ (D) .①②
x2 16y2
8.若双曲线 2 1的左焦点在抛物线 y
2 2px的准线上,则 p的值为 ( )
3 p
A. 2 B. 3 C. 4 D. 4 2
9.如图,正方体 ABCD A1B1C1D1 的棱长为 1,O 是底面
A1B1C1D1的中心,则点 O 到平面 ABC1D1的距离为( )
(A) .1 (B) . 2 (C) . 2 (D) . 3
2 4 2 2
x2 y2
10.若双曲线 2 2 1 ( a 0,b 0 )的右支上到原点和右焦点距离相等的点有两个, 则a b
双曲线离心率的取值范围是 ( )
(A) . e 2 (B) . 1 e 2 (C) . e 2 (D) .1 e 2
11. C y 2 4x y 2对于抛物线 : ,我们称满足 0 4x0 的点M (x0 , y0 )在抛物线的内部.若点
M (x0 , y0 )在抛物线内部,则直线 l : y0 y 2(x x0 ) 与曲线 C ( )
(A) . 恰有一个公共点 (B) . 恰有 2 个公共点
(C) . 可能有一个公共点,也可能有两个公共点 (D) . 没有公共点
x2 y2
12.已知 F1 、F2 是椭圆 2 2 1( a b 0 )的两个焦点, P是椭圆上任意一点,从任一焦a b
点引 F1PF2 的外角平分线的垂线,垂足为Q , 则点Q的轨迹 ( )
(A) . 圆 (B) . 椭圆 (C) . 双曲线 (D) . 抛物线
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.已知命题 p: x∈R,x2+x+1>0,则 p 为 。
14.2021 年 2 月某地发生新冠肺炎疫情,急需从一所三甲医院的呼吸科抽调部分医生参加救
援,该呼吸科共有男女医生各 10 人,要求抽调的女医生至少有 1 人,男医生至少比女医生
多 2 人,为了保证该院呼吸科的正常运转,从该院呼吸科抽调的医生人数不能超过 10 人。
已知每名男医生一天可以给 40 名病人进行康复治疗,每名女医生一天可以给 35 名病人进行
康复治疗,那么应该从该呼吸科抽调男医生 人,女医生 人,从而使
每天获得康复治疗的病人最多。
15.在等比数列{an}中,a5-a3=12,a6-a4=24,记数列{an}的前 n 项和、前 n 项积分别为 Sn,
Sn 1
2
Tn,则 n= 时, 的值最大。
Tn
B C
16.在△ABC 中,角 A,B,C 所对应的边分别为 a,b,c, 3 bsin =asinB,△ABC 的
2
外接圆面积为 12π,则△ABC 面积的最大值是 。
三、解答题(本大题共 6个小题,共 70分)
17.(本题 10 分)如图所示,在空间四边形 ABCD中, E, F分别为 AB, AD的中点,G,
H 分别在BC,CD上,且BG :GC DH :HC 1: 2.求证:(1)E、F、G、H 四点共面;
(2) EG与HF的交点在直线 AC上.
18.在四棱锥 P﹣ABCD 中,∠ABC=∠ACD=90°,∠
BAC=∠CAD=60°,PA⊥平面 ABCD,E 为 PD 的中点,PA=2AB=2.求:
(1)求四棱锥 P﹣ABCD 的体积 V;
(2)若 F 为 PC 的中点,求证 PC⊥平面 AEF.
19.(本题 12 分)抚州市为了了解学生的体能情况,从全市所有高一学生中按 80:1 的比例
随机抽取 200 人进行一分钟跳绳次数测试,将所得数据整理后,分为6组画出频率分布直方
图 (如图所示 ),现一,二两组数据丢失,但知道第二组的频率是第一组的 3 倍.
(1)若次数在120以上 (含120次 )为优秀,试估计全市高一学生的优秀率是多少?全市优秀
学生的人数约为多少?
(2)求第一组、第二小组的频率是多少?并补齐频率分布直方图;
(3)估计该全市高一学生跳绳次数的中位数和平均数?
20.(本题 12 分)如图,四边形 ABCD是正方形,四边形 BEDF是菱形,平面 ABCD 平面
BEDF BD .
(1)证明: AE BD;
(2)若 AB BE,且平面 ABCD 平面 BEDF,求平面 ADE与平面 CDF所成的二面角的
正弦值.
21.(本题 12 分)某保险公司根据官方公布的历年营业收入,制成表格如下:
表 1
年份 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020
年份序号 x 1 2 3 4 5 6 7 8 9 10
营业收入 y(亿元) 0.52 9.36 33.6 132 352 571 912 1207 1682 2135
由表 1,得到下面的散点图:
根据已有的函数知识,某同学选用二次函数模型 y bx2 a(b和 a是待定参数)来拟合 y
和 x的关系.这时,可以对年份序号做变换,即令 t x2 ,得 y bt a,由表 1 可得变换后的
数据见表 2.
表 2
t 1 4 9 16 25 36 49 64 81 100
y 0.52 9.36 33.6 132 352 571 912 1207 1682 2135
(1)根据表中数据,建立 y关于 t的回归方程(系数精确到个位数);
(2)根据(1)中得到的回归方程估计 2021 年的营业收入,以及营业收入首次超过 4000
亿元的年份.
附:对于一组数据 u1,v1 , u2 ,v2 , , un ,vn ,其回归直线 v u 的斜率和截距的最小二
n
ui u vi v
乘估计分别为 i 1 n , v u .
2 ui u
i 1
10 2 10
参考数据: t 38.5, y 703.45, t i t 1.051 10 4, t i t y i y 2.327 10 5 .
i 1 i 1
22.(本题 12 分)如图,在三棱柱 ABC A1B1C1中, BB1 平面 ABC, AB BC,
AA1 AB BC 2 .
(1)求证:BC1 平面 A1B1C;
B M 1
(2)点 M BC 1在线段 1 上,且 B C 3 ,试问在线段 A1B上是否存在一点 N,满足MN // 平面1
AN
A1ACC
1
1 ,若存在求 AB 的值,若不存在,请说明理由?1
理科数学答案
题号 1 3 4 5 6 7 8 9 10 11 12
答案 A B B A D B C B C D A
17.(1)证明见解析;(2)证明见解析.
证明(1)∵BG :GC DH :HC,∴GH //BD. --------1 分
∵ E, F分别为 AB, AD的中点, --------3 分
∴ EF //BD,∴ EF //GH ,∴ E, F,G,H四点共面. --------5 分
(2)∵G,H不是 BC,CD的中点,
∴ EF //GH ,且 EF GH ,故 EFHG为梯形.
∴ EG与 FH 必相交,设交点为M , -------6 分
∴ EG 平面 ABC,FH 平面 ACD,
∴M 平面 ABC,且M 平面 ACD, -------8 分
∴M AC,即GE与HF的交点在直线 AC上. -------10 分
18 5 3.(1) ,(2)见解析.
3
试题解析:
(1)在 Rt ABC中, AB 1, BAC 60 , BC 3, AC 2 .
在 Rt ACD中 AC 2, CAD 60 , ---------2 分
CD 2 3, AD 4, S 1 1ABCD AB·BC AC·CD --------4 分2 2
1 1 5
1 3 2 2 3 3 .
2 2 2
V 1 5 3 2 5则 3 . ---------6 分
3 2 3
(2) PA CA, F为 PC的中点, AF PC .
PA 平面 ABCD, PA CD . ---------8 分
AC CD,PA AC A, CD 平面 PAC, CD PC .
E为 PD中点,F 为 PC为中点, EF CD,则 EF PC . --------10 分
AF EF F , PC 平面 AEF . --------12 分
考点:四棱锥的体积公式;直线与平面垂直的判定与证明.
19.(1)8640;(2)第一组频率为0.03,第二组频率为0.09 .频率分布直方图见解析;(3)
334
中位数为 ,均值为 121.9
3
(1)由频率分布直方图,分数在 120 分以上的频率为 (0.030 0.018 0.006) 10 0.54,
因此优秀学生有0.54 200 80 8640(人); -------4 分
(2)设第一组频率为 x,则第二组频率为3x,
所以 x 3x 0.34 0.54 1, x 0.03,
第一组频率为0.03,第二组频率为0.09 . -------6 分
频率分布直方图如下: -------8 分
(3)前 3 组数据的频率和为 (0.003 0.009 0.034) 10 0.46,中位数在第四组,
n n 110设中位数为 ,则 0.3 0.46 0.5, n 334 . ------10 分
120 110 3
均值为0.03 95 0.09 105 0.34 115 0.3 125 0.18 135 0.06 145 121.9.------12 分
20 1 2 2 2.( )证明见解析;( ) .
3
(1)证明:如图,连接 AC交 BD于点O,连接OE.
四边形 ABCD为正方形,
BD OA,且O为BD的中点.
又 四边形BEDF为菱形,
BD OE. -------2 分
∵OA OE O,OA,OE 平面OAE,
BD 平面OAE, -------4 分
又 AE 平面 OAE
BD AE. --------6 分
(2)解:如图,建立空间直角坐标系,不妨设 AB 2 ,
则 BD 2 2 ,OE 2 ,
则 A(2,0,0),D(0,0,0),C(0, 2,0).
由(1)得OE BD,
又 平面 ABCD 平面 BEDF,平面 ABCD 平面 BEDF BD,
OE 平面 ABCD,故 E(1,1, 2),同理F (1,1, 2) ,
DA (2,0,0),DE (1,1, 2),DC (0, 2,0),DF (1,1, 2). ------8 分
m (x 设 1, y1, z1)为平面DAE的法向量, n (x2 , y2 , z2 )为平面DCF的法向量,
m ·DA 2x1 0,
则 故可取m (0, 2,1),
m·DE x1 y1 2z1 0,
n ·DC 2y2 0,
同理 故可取 n ( 2,0,1), -------10 分
n·DF x2 y2 2z2 0,
m ·n 1 1
所以 cos m,n m n 3 3 3 .
2
设平面 ADE与平面CDF所成的二面角为 1 2 2,则 sin 1 ,
3 3
所以平面 ADE与平面CDF 2 2所成的二面角的正弦值为 . -------12 分
3
21.(1) y 22t 144 ;(2)估计 2021 年的营业收入约为 2518 亿元,估计营业收入首次超
过 4000 亿元的年份为 2024 年.
10
ti t yi y
b i 1 2.327 10
5
(1) 10 22, --------3 分
t t 2 1.051 10
4
i
i 1
a y b t 703.45 22 38.5 144 , --------5 分
故回归方程为 y 22t 144 . --------6 分
(2)2021 年对应的 t的值为 121,营业收入 y 22 121 144 2518,
所以估计 2021 年的营业收入约为 2518 亿元. -------8 分
依题意有 22t 144 4000,解得 t 188.4,故 x2 188.4 .
因为13 188.4 14, -------10 分
所以估计营业收入首次超过 4000 亿元的年份序号为 14,即 2024 年.--------12 分
AN 2
22.(1 1)证明见解析;(2)存在, AB 的值为 .1 3
(1)在三棱柱 ABC A1B1C1中, BB1 平面 ABC, AB BC, AA1 AB BC 2 .
∴ BC1 B1C,BB1 A1B1, A1B1 B1C1,
∵ BB1 B1C1 B1 , ------2 分
∴ A1B1 平面 BBC1B1,
∵BC1 平面 BBC1B1,
∴ A1B1 BC1, -------4 分
∵ A1B1 B1C B1 ,
∴BC1 平面 A1B1C . -------5 分
(2)以 B为原点, BC为 x轴, BA为 y轴, BB1 为轴,建立空间直角坐标系,如图,
A 0,2,0 C 2,0,0 C1 2,0, 2 , B 0,0,0 , B1 0,0,2 , A1 0, 2, 2 ,
所以CA 2, 2,0 ,CC 0,0, 2 , --------7 分1
n C A 2x 2y 0设平面 ACC1A1 的法向量 n x, y, z ,则 n
,
CC1 2z 0
取 x 1,得 n 1,1,0 , --------8 分
B M 1
点 M BC 1在线段 1 上,且 A BB C 3 ,点 N在线段 1 上,设M a,b,c , N x, y, z ,1
A1N 设 A B ,则 B1C 3B M,1 A N A B, 0≤ ≤1,1 11
即 2,0, 2 3 a,b,c 2 , x, y 2, z 2 0, 2, 2
M 2 ,0, 4 解得 , N 0,2 2 , 2 2 3 3 ,
MN 2 , 2 2 ,
2
2 , -------10 分
3 3
∵MN //平面A1ACC1,
2 AN
∴ n MN 2 2 0
2 1 2
,解得 .∴ 的值为 . --------12 分
3 3 A1B 3
同课章节目录
