四川省成都高新区2013届高三11月检测数学(理)试题
文档属性
| 名称 | 四川省成都高新区2013届高三11月检测数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 350.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-13 18:50:33 | ||
图片预览




文档简介
一、选择题(每小题5分,共50分)
1.设i为虚数单位,复数的共轭复数为( )
A.2+i B.2-i C.-1+2i D.-1-2i
2.设全集U是实数集R,,则图中阴影部分所表示的集合是( )
A. B.
C. D.
3.下列命题正确的是( )
A. B.
C.若 D 的充分不必要条件
4.设X、Y、Z是空间不同的直线或平面,对下面四种情形,使“X⊥Z且Y⊥ZX//Y”为真命题的是( )
①X、Y、Z是直线;②X、Y是直线,Z是平面;③Z是直线,X、Y是平面;④X、Y、Z是平面
A.①② B.②③ C.①③ D.③④
5.给出下面类比推理命题:
①“若,则”类推出“若,则”;
②“若”类推出“”
③“”类推出“”
④“”类推出“”其中类比结论正确的个数为( )
A.1 B.2 C.3 D.4
6.将4名新来的同学分配到A、B、C三个班级中,每个班级至少安排1名学生,其中甲同学不能分配到A班,那么不同的分配方案有( )
A.18种 B.54种 C.60种 D.24种
7.已知①为函数的图象,则图②中的图象对应的函数可能是( )
A. B.
C. D.
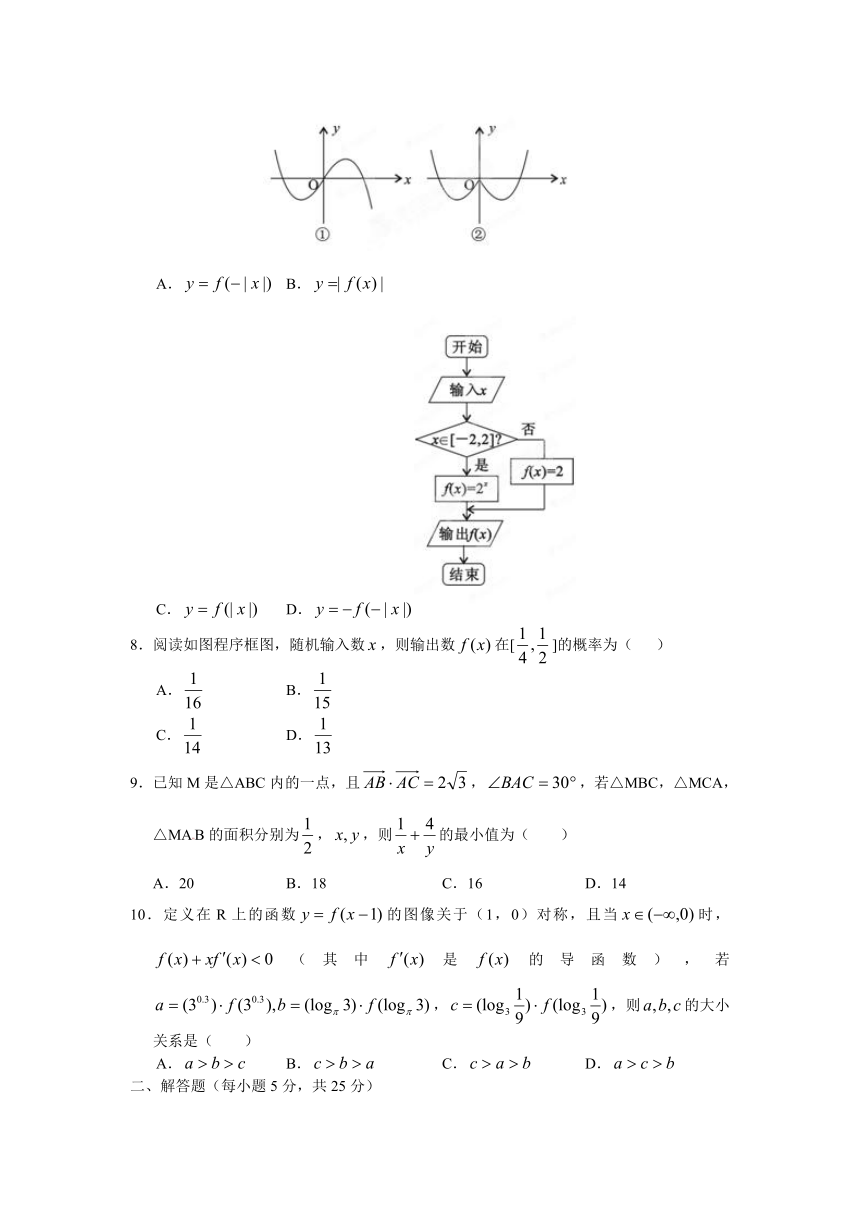
8.阅读如图程序框图,随机输入数,则输出数在[]的概率为( )
A. B.
C. D.
9.已知M是△ABC内的一点,且,,若△MBC,△MCA,△MAB的面积分别为,,则的最小值为( )
A.20 B.18 C.16 D.14
10.定义在R上的函数的图像关于(1,0)对称,且当时,(其中是的导函数),若,,则的大小关系是( )
A. B. C. D.
二、解答题(每小题5分,共25分)
11.的展开式中含项的系数为10,则实数a为____________
12.数列的前n项和为,,则数列中取得最大值的项是第_______项
13.某所学校计划招聘男教师x名,女教师y名,x和y必须满足约束条件,则该校招聘的教师人数最多是_______名。
14.四位同学在研究函数时,分别给出下面四个结论:
①函数的图象关于轴对称;②若,则一定有;
③函数的值域为(-1,1);④若规定
则对任意恒成立,你认为上述四个结论中正确的有_____
15.选做题(请在以下两题中任选一题作答,若两题都做,只计(1)题分)
(1)在极坐标系中,圆的圆心到直线的距离是_______
(2)已知命题p:“对任意的”,命题q:“存在”若命题“p且q”是真命题,则实数a的取值范围是_____
三、解答题(共75分)
16.(12分)某品牌车商为了在成都车展中树立其良好形象,车商决定从参聘的12名男志愿者和18名女志愿者中挑选出宣传人员,这30名志愿者的身高如下:单位:cm
若身高在175cm(含175cm)以上,定义为“高个子”,身高在175cm以下,定义为“非高个子”且只有“女高个子”才能担任“车模”
(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,那么至少有1人是“高个子”的概率是多少。
(2)若从所有“高个子”中选3名志愿者,用表示所选志愿者中能担任“车模”的人数,试写出的分布列,并求。
17.(12分)边长为的正方形SBAC,沿对角线BC翻折成如图所示的三棱锥S—ABC,且SA=,O为BC的中点。
(1)证明:平面SBC⊥平面ABC
(2)求二面角A—SC—B的余弦值。
18.(12分)函数在一个周期内的图象,如图,A为最高点,B、C为图象与x轴的交点,△ABC为正三角形
(1)求及值域;
(2)若,求的值。
19.(12分)工厂生产某种产品,次品率P与日产量x(万件)间的关系为其中函数的图象可由函数的图象向右平移6个单位而得,已知每生产1件合格产品盈利3元,每出现一件次品亏损1.5元。
(1)将日盈利额(万元)表示为日产量(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?
(注:次品率=)
20.(13分)已知是一个公差大于0的等差数列,且满足。数列是首项为1,公比为的等比数列。
(1)求数列的通项公式;
(2)求数列的通项公式,并求其前n项和Tn。
(3)若,求数列的前n项和Sn
21.(14分)已知函数,为实数)
(1)当时,求函数在上的最小值;
(2)若方程(其中)在区间上有解,求实数的取值范围;
(3)证明:(参考数据:
答案(理科)
(2)
=
……………………12分
同课章节目录
