2021-2022学年高二下学期数学人教A版选修2-3 1.1 分类加法计数原理与分步乘法计数原理 随堂检测(Word含解析)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版选修2-3 1.1 分类加法计数原理与分步乘法计数原理 随堂检测(Word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 93.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-17 00:00:00 | ||
图片预览

文档简介
1.1 分类加法计数原理与分步乘法计数原理-2021-2022学年高二数学人教A版选修2-3随堂检测
1.5名运动员争夺3项比赛冠军(每项比赛无并列冠军),获得冠军的可能种数为( )
A. B. C. D.
2.从1,2,3,4,5,6,7,8,9这9个数字中任取两个,其中一个作为底数,另一个作为真数,则可以得到不同对数值的个数为( )
A.64 B.56 C.53 D.51
3.如图所示,积木拼盘由A,B,C,D,E五块积木组成,若每块积木都要涂一种颜色,且为了体现拼盘的特色,相邻的区域需涂不同的颜色(如:A与B为相邻区域,A与D为不相邻区域),现有五种不同的颜色可供挑选,则不同的涂色方法的种数是( )
A.780 B.840 C.900 D.960
4.某旅行社共有5名专业导游,其中3人会英语,3人会日语,若在同一天要接待3个不同的外国旅游团,其中有2个旅游团要安排会英语的导游,1个旅游团要安排会日语的导游,则不同的安排方法种数有( )
A.12 B.13 C.14 D.15
5.某校高一年级有四个班,四位老师各教一个班的数学在该年级某次数学考试中,要求每位数学老师均不在本班监考,则不同的安排监考的方法种数为( )
A.8 B.9 C.12 D.24
6.某新闻采访组由5名记者组成,其中甲、乙、丙、丁为成员,戊为组长.甲、乙、丙、丁分别来自A,B,C,D四个地区.现在该新闻采访组要到A,B,C,D四个地区去采访,在安排采访时要求:一地至少安排一名记者采访且组长不单独去采访;若某记者要到自己所在地区采访时必须至少有一名记者陪同.则所有采访的不同安排方法有___________种.
7.有A,B,C三个城市,每天上午从A城去B城有5班汽车,2班火车,都能在12:00前到达B城,下午从B城去C城有3班汽车,2班轮船.某人上午从A城出发去B城,要求12:00前到达,下午从B城去C城,则不同的走法有__________种.
8.如图所示,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端异色,如果只有5种颜色可供使用,求不同的染色方法种数.
答案以及解析
1.答案:D
解析:每1项冠军的情况都有5种,故5名学生争夺3项冠军,获得冠军的可能的种数是.故选D.
2.答案:C
解析:由于1只能作为真数,则以1为真数,从其余各数中任取一数为底数,对数值均为0,
从除1外的其余各数中任取两数分别作为对数的底数和真数,共能组成个对数式,
其中,,,,,重复了4次,
所以得到不同对数值的个数为.
故选:C
3.答案:D
解析:解:先涂A,则A有种涂法,再涂B,因为B与A相邻,所以B的颜色只要与A不同即可,有种涂法,同理C有种涂法,D有种涂法,E有种涂法,由分步乘法计数原理,可知不同的涂色方法种数为.
故选:D.
4.答案:C
解析:由题意知有1名导游既会英语又会日语,记甲为既会英语又会日语的导游,按照甲是否被安排到需要会英语的旅游团可分为两类:
第一类,甲被安排到需要会英语的旅游团,则可分两步进行:
第一步,从会英语的另外2人中选出1人,有2种选法,将选出的人和甲安排到2个需要会英语的旅游团,有2种安排方法,所以有种安排方法;
第二步,从会日语的另外2人中选出1人安排到需要会日语的旅游团,共2种选法.
故此时共有种安排方法;
第二类,甲没有被安排到需要会英语的旅游团,则可分两步进行:
第一步,将会英语的另外2人安排到需要会英语的旅游团,有2种安排方法;
第二步,从会日语的3人(包括甲)中选出1人安排到需要会日语的旅游团,有3种选法.
故此时共有种选法.
综上,不同的安排方法种数为.
故选:C.
5.答案:B
解析:设四个班分别是A、B、C、D,对应的数学老师分别是a、b、c、d.
让a老师先选,可从B、C、D班中选一个,有3种选法,
不妨假设a老师选的是B,则b老师从剩下的三个班级中任选一个,有3种选法,剩下的两位老师都只有1种选法.
由分步乘法计数原理,知共有种不同的安排方法.
故选:B.
6.答案:44
解析:分两类:
①甲,乙,丙,丁都不到自己的地区,组长可任选一地有;
②甲,乙,丙,丁中只一人到自己的地区,并有组长陪同有.
所以总数.
故答案为:44.
7.答案:35
解析:由题意,知从A城到B城的走法有(种);从B城到C城的走法有(种).故不同的走法有(种).
8.答案:方法一按S,A,B,C,D的顺序分步染色.
第一步,S点染色,有5种方法;
第二步,A点染色,与S在同一条棱上,有4种方法;
第三步,B点染色,与S,A分别在同一条棱上,有3种方法;
第四步,C点染色,但考虑到D点与S,A,C分别在同一条棱上,需要针对A与C是否同色进行分类,当A与C同色时,D点有3种染色方法;当A与C不同色时,因为C与S,B也不同色,所以C点有2种染色方法,D点也有2种染色方法.
由分步乘法分类加法计数原理,得不同的染色方法种数为.
方法二按所用颜色种数分类.
第一类,5种颜色全用,共有种不同的方法;
第二类,只用4种颜色,则必有某两个顶点同色(A与C或B与D),共有种不同的方法;
第三类,只用3种颜色,则A与C,B与D必定同色,共有种不同的方.
由分类加法计数原理,得不同的染色方法种数为.
1.5名运动员争夺3项比赛冠军(每项比赛无并列冠军),获得冠军的可能种数为( )
A. B. C. D.
2.从1,2,3,4,5,6,7,8,9这9个数字中任取两个,其中一个作为底数,另一个作为真数,则可以得到不同对数值的个数为( )
A.64 B.56 C.53 D.51
3.如图所示,积木拼盘由A,B,C,D,E五块积木组成,若每块积木都要涂一种颜色,且为了体现拼盘的特色,相邻的区域需涂不同的颜色(如:A与B为相邻区域,A与D为不相邻区域),现有五种不同的颜色可供挑选,则不同的涂色方法的种数是( )
A.780 B.840 C.900 D.960
4.某旅行社共有5名专业导游,其中3人会英语,3人会日语,若在同一天要接待3个不同的外国旅游团,其中有2个旅游团要安排会英语的导游,1个旅游团要安排会日语的导游,则不同的安排方法种数有( )
A.12 B.13 C.14 D.15
5.某校高一年级有四个班,四位老师各教一个班的数学在该年级某次数学考试中,要求每位数学老师均不在本班监考,则不同的安排监考的方法种数为( )
A.8 B.9 C.12 D.24
6.某新闻采访组由5名记者组成,其中甲、乙、丙、丁为成员,戊为组长.甲、乙、丙、丁分别来自A,B,C,D四个地区.现在该新闻采访组要到A,B,C,D四个地区去采访,在安排采访时要求:一地至少安排一名记者采访且组长不单独去采访;若某记者要到自己所在地区采访时必须至少有一名记者陪同.则所有采访的不同安排方法有___________种.
7.有A,B,C三个城市,每天上午从A城去B城有5班汽车,2班火车,都能在12:00前到达B城,下午从B城去C城有3班汽车,2班轮船.某人上午从A城出发去B城,要求12:00前到达,下午从B城去C城,则不同的走法有__________种.
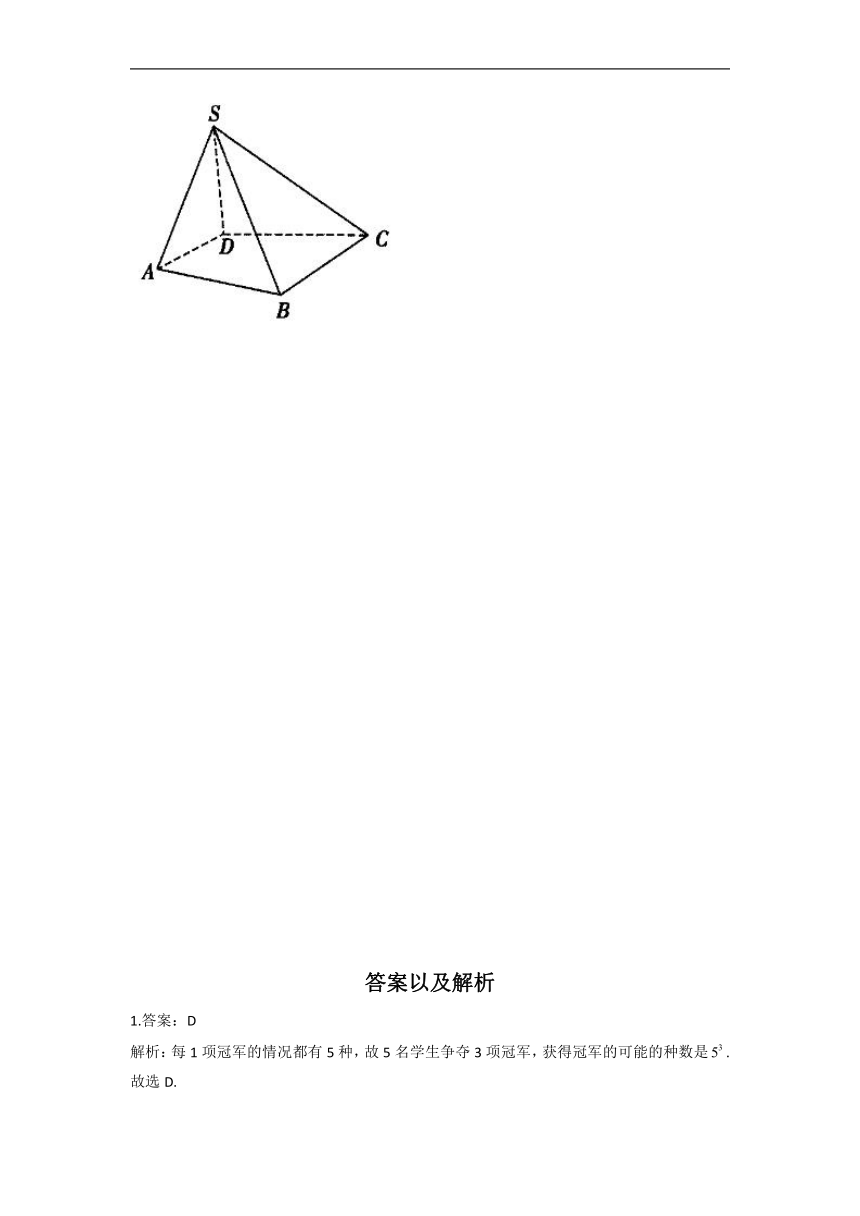
8.如图所示,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端异色,如果只有5种颜色可供使用,求不同的染色方法种数.
答案以及解析
1.答案:D
解析:每1项冠军的情况都有5种,故5名学生争夺3项冠军,获得冠军的可能的种数是.故选D.
2.答案:C
解析:由于1只能作为真数,则以1为真数,从其余各数中任取一数为底数,对数值均为0,
从除1外的其余各数中任取两数分别作为对数的底数和真数,共能组成个对数式,
其中,,,,,重复了4次,
所以得到不同对数值的个数为.
故选:C
3.答案:D
解析:解:先涂A,则A有种涂法,再涂B,因为B与A相邻,所以B的颜色只要与A不同即可,有种涂法,同理C有种涂法,D有种涂法,E有种涂法,由分步乘法计数原理,可知不同的涂色方法种数为.
故选:D.
4.答案:C
解析:由题意知有1名导游既会英语又会日语,记甲为既会英语又会日语的导游,按照甲是否被安排到需要会英语的旅游团可分为两类:
第一类,甲被安排到需要会英语的旅游团,则可分两步进行:
第一步,从会英语的另外2人中选出1人,有2种选法,将选出的人和甲安排到2个需要会英语的旅游团,有2种安排方法,所以有种安排方法;
第二步,从会日语的另外2人中选出1人安排到需要会日语的旅游团,共2种选法.
故此时共有种安排方法;
第二类,甲没有被安排到需要会英语的旅游团,则可分两步进行:
第一步,将会英语的另外2人安排到需要会英语的旅游团,有2种安排方法;
第二步,从会日语的3人(包括甲)中选出1人安排到需要会日语的旅游团,有3种选法.
故此时共有种选法.
综上,不同的安排方法种数为.
故选:C.
5.答案:B
解析:设四个班分别是A、B、C、D,对应的数学老师分别是a、b、c、d.
让a老师先选,可从B、C、D班中选一个,有3种选法,
不妨假设a老师选的是B,则b老师从剩下的三个班级中任选一个,有3种选法,剩下的两位老师都只有1种选法.
由分步乘法计数原理,知共有种不同的安排方法.
故选:B.
6.答案:44
解析:分两类:
①甲,乙,丙,丁都不到自己的地区,组长可任选一地有;
②甲,乙,丙,丁中只一人到自己的地区,并有组长陪同有.
所以总数.
故答案为:44.
7.答案:35
解析:由题意,知从A城到B城的走法有(种);从B城到C城的走法有(种).故不同的走法有(种).
8.答案:方法一按S,A,B,C,D的顺序分步染色.
第一步,S点染色,有5种方法;
第二步,A点染色,与S在同一条棱上,有4种方法;
第三步,B点染色,与S,A分别在同一条棱上,有3种方法;
第四步,C点染色,但考虑到D点与S,A,C分别在同一条棱上,需要针对A与C是否同色进行分类,当A与C同色时,D点有3种染色方法;当A与C不同色时,因为C与S,B也不同色,所以C点有2种染色方法,D点也有2种染色方法.
由分步乘法分类加法计数原理,得不同的染色方法种数为.
方法二按所用颜色种数分类.
第一类,5种颜色全用,共有种不同的方法;
第二类,只用4种颜色,则必有某两个顶点同色(A与C或B与D),共有种不同的方法;
第三类,只用3种颜色,则A与C,B与D必定同色,共有种不同的方.
由分类加法计数原理,得不同的染色方法种数为.
