2.3等差数列前n项和公式课件-2021-2022学年高二下学期数学人教A版必修5 (1)(共27张PPT)
文档属性
| 名称 | 2.3等差数列前n项和公式课件-2021-2022学年高二下学期数学人教A版必修5 (1)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
等差数列的前n项和公式及应用
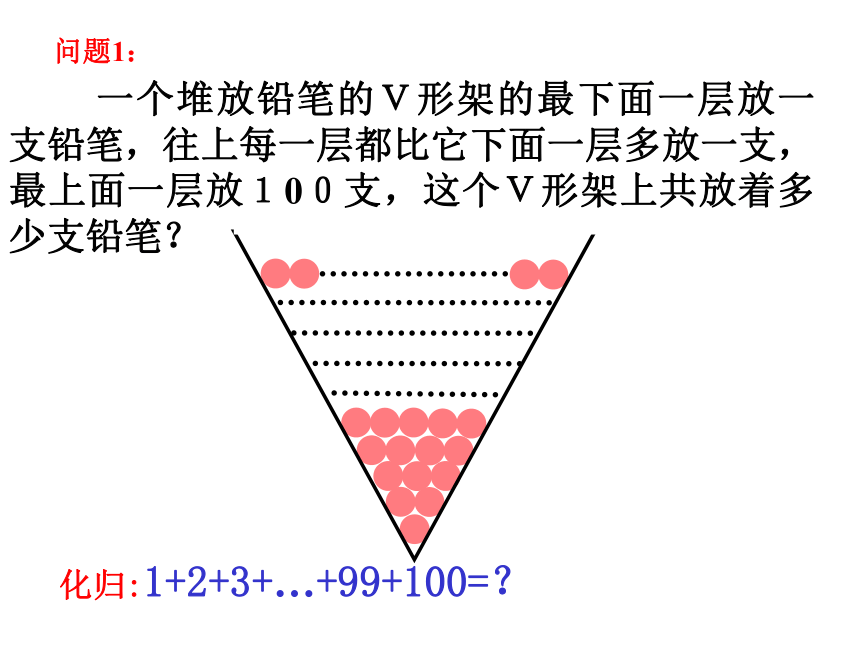
一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支,这个V形架上共放着多少支铅笔?
化归:1+2+3+…+99+100=?
问题1:
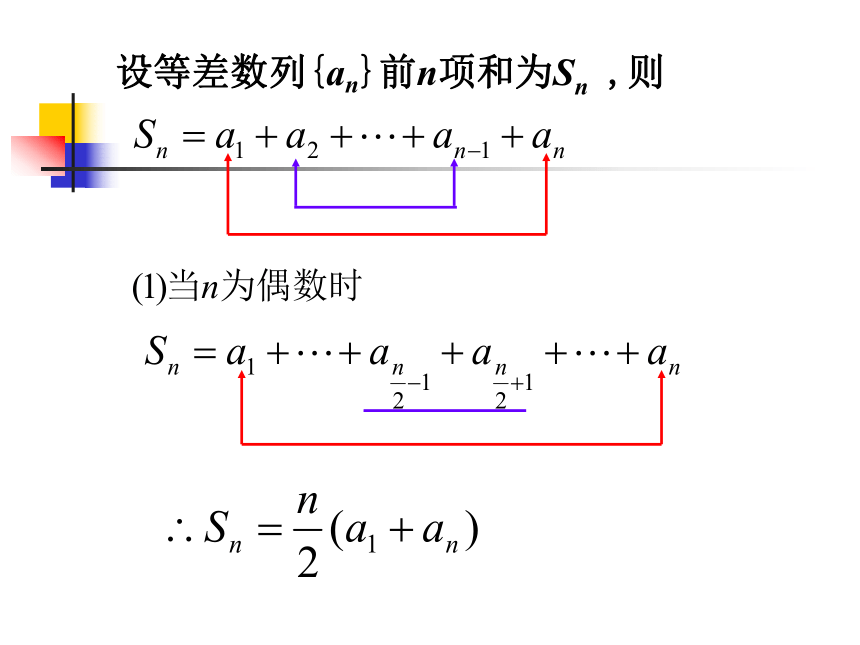
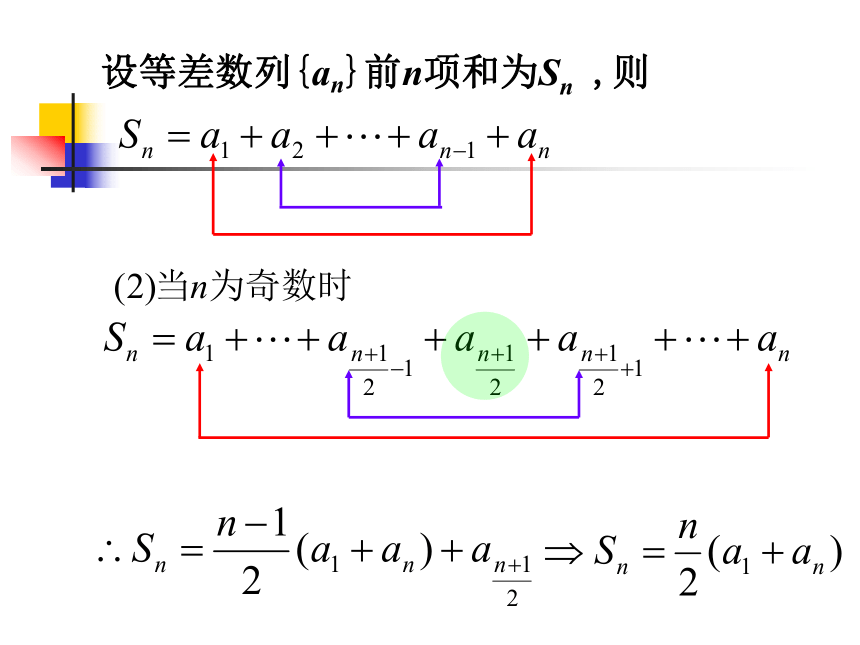
设等差数列{an}前n项和为Sn ,则
设等差数列{an}前n项和为Sn ,则
①
②
又
又
∴
(算法:倒序相加求和;
用到了等差数列的性质)
① +
②
1.推导公式:
1.推导公式(教材):
① +
②
①
②
2.记忆公式
2.记忆公式
3.剖析公式:
共5个量,由三个公式联系
,知三可求二.
通项公式
4. 公式的应用
例1、计算:
(1)1+2+3+…+n
(2)1+3+5+…+(2n-1)
(3)2+4+6+…+2n
(4)1-2+3-4+5-6+…+(2n-1)-2n
1
2
3
n
(1)1+2+3+…+n=
例1解答:
1
n
n-1
n-2
(2) 1+3+5+…+(2n-1)=
(3) 2+4+6+…+2n= .
例1解答:
(4)1-2+3-4+5-6+...+(2n-1)-2n
原式=[1+3+5+…+(2n-1)]-(2+4+6+...+2n)
= n2 -n(n+1)
=-n
原式=-1-1-…-1=-n
法1.
法2.
方程思想知三求一
例2.等差数列-10,-6,-2,2,…的前
多少项的和是54 ? ?
由
代入
化简得
思路:
(1)解:由已知可得:
整体思想认识公式
例3. 在等差数列{an} 中
(1)
已知:
求:
(2)
已知:
,求:
36
15
12
5
2
=
+
+
+
a
a
a
a
(2) 解:
例3. 在等差数列{an} 中
(1)
已知:
求:
(2)
已知:
,求:
36
15
12
5
2
=
+
+
+
a
a
a
a
思考:
与 的关系
即有奇数项的等差数列的前 项的和等于中间 项 的 倍 。 ,
思考:
与 的关系
5.函数的角度认识公式:
公式2可化为:
若令
,
当
,即
时,
上式是关于 的二次函数,
且常数项为零.
它的图象是抛物线上的离散点。
例2.等差数列-10,-6,-2,2,…的前多少项的和是54 ? ?
5.函数的角度认识公式:
思考1:
2.
若 是等差数列,则其前 项和是关于 的
函数,形如 ,
反过来也成立吗?
等差数列的前 项和 何时有最大值,最小值?如何求 ?有哪些方法 ?
3.
教材例4还有其它解法吗
小结:
回顾从特殊到一般,一般到特殊的研究方法;
体会等差数列的基本元表示方法,倒序相加的算法,及数形结合的数学思想;
掌握等差数列的两个求和公式及简单应用。
学会用函数的观点分析数列。
作业:
教材练习做书上
习题 1—4(作业本)
等差数列的前n项和公式及应用
一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支,这个V形架上共放着多少支铅笔?
化归:1+2+3+…+99+100=?
问题1:
设等差数列{an}前n项和为Sn ,则
设等差数列{an}前n项和为Sn ,则
①
②
又
又
∴
(算法:倒序相加求和;
用到了等差数列的性质)
① +
②
1.推导公式:
1.推导公式(教材):
① +
②
①
②
2.记忆公式
2.记忆公式
3.剖析公式:
共5个量,由三个公式联系
,知三可求二.
通项公式
4. 公式的应用
例1、计算:
(1)1+2+3+…+n
(2)1+3+5+…+(2n-1)
(3)2+4+6+…+2n
(4)1-2+3-4+5-6+…+(2n-1)-2n
1
2
3
n
(1)1+2+3+…+n=
例1解答:
1
n
n-1
n-2
(2) 1+3+5+…+(2n-1)=
(3) 2+4+6+…+2n= .
例1解答:
(4)1-2+3-4+5-6+...+(2n-1)-2n
原式=[1+3+5+…+(2n-1)]-(2+4+6+...+2n)
= n2 -n(n+1)
=-n
原式=-1-1-…-1=-n
法1.
法2.
方程思想知三求一
例2.等差数列-10,-6,-2,2,…的前
多少项的和是54 ? ?
由
代入
化简得
思路:
(1)解:由已知可得:
整体思想认识公式
例3. 在等差数列{an} 中
(1)
已知:
求:
(2)
已知:
,求:
36
15
12
5
2
=
+
+
+
a
a
a
a
(2) 解:
例3. 在等差数列{an} 中
(1)
已知:
求:
(2)
已知:
,求:
36
15
12
5
2
=
+
+
+
a
a
a
a
思考:
与 的关系
即有奇数项的等差数列的前 项的和等于中间 项 的 倍 。 ,
思考:
与 的关系
5.函数的角度认识公式:
公式2可化为:
若令
,
当
,即
时,
上式是关于 的二次函数,
且常数项为零.
它的图象是抛物线上的离散点。
例2.等差数列-10,-6,-2,2,…的前多少项的和是54 ? ?
5.函数的角度认识公式:
思考1:
2.
若 是等差数列,则其前 项和是关于 的
函数,形如 ,
反过来也成立吗?
等差数列的前 项和 何时有最大值,最小值?如何求 ?有哪些方法 ?
3.
教材例4还有其它解法吗
小结:
回顾从特殊到一般,一般到特殊的研究方法;
体会等差数列的基本元表示方法,倒序相加的算法,及数形结合的数学思想;
掌握等差数列的两个求和公式及简单应用。
学会用函数的观点分析数列。
作业:
教材练习做书上
习题 1—4(作业本)
