北师大版八年级下册1.3线段的垂直平分线同步练习(word版含答案)
文档属性
| 名称 | 北师大版八年级下册1.3线段的垂直平分线同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 265.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-15 22:15:18 | ||
图片预览

文档简介
北师大版同步检测卷:线段的垂直平分线
一、选择题(共10小题;共50分)
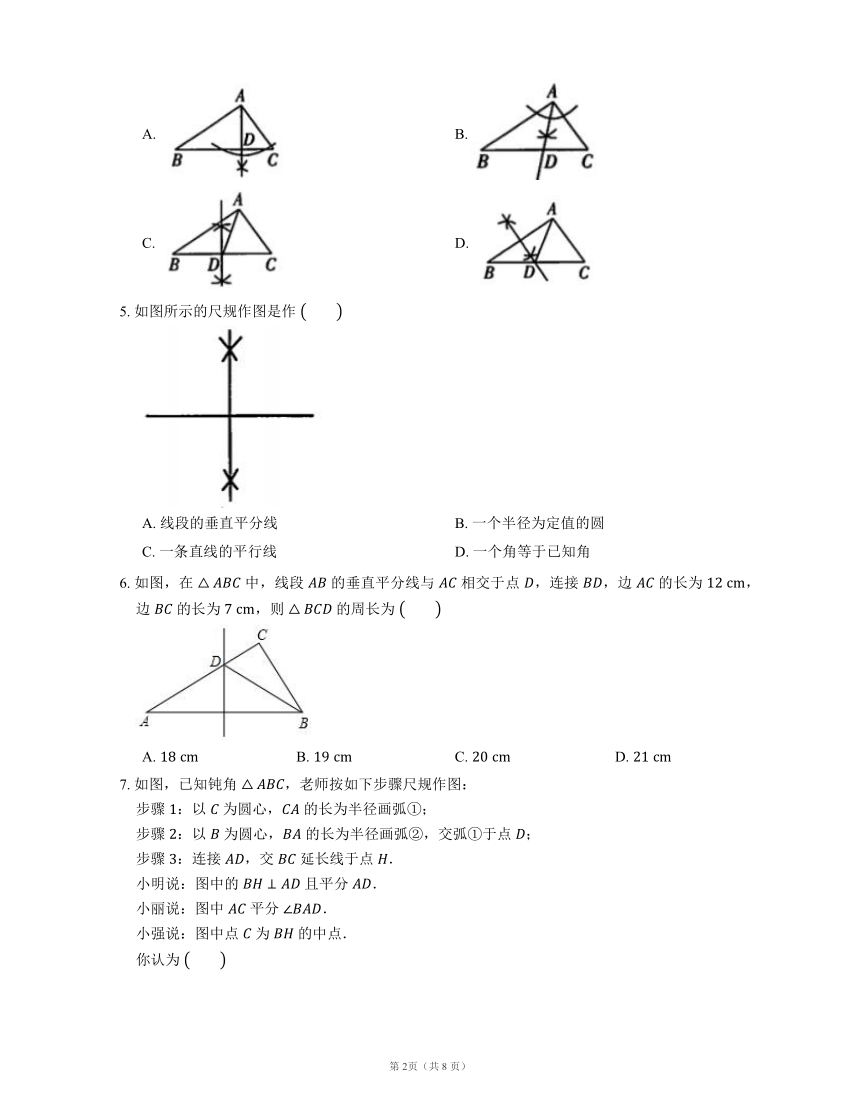
1. 通过如下尺规作图,能确定点 是 边中点的是
A. B.
C. D.
2. 如图,在 中, 的垂直平分线交 于点 ,交 于点 ,若 ,,则 的周长为
A. B. C. D.
3. 如图,,,则有
A. 与 互相垂直平分 B. 垂直平分
C. 垂直平分 D. 平分
4. 以下尺规作图中,一定能得到线段 的是
A. B.
C. D.
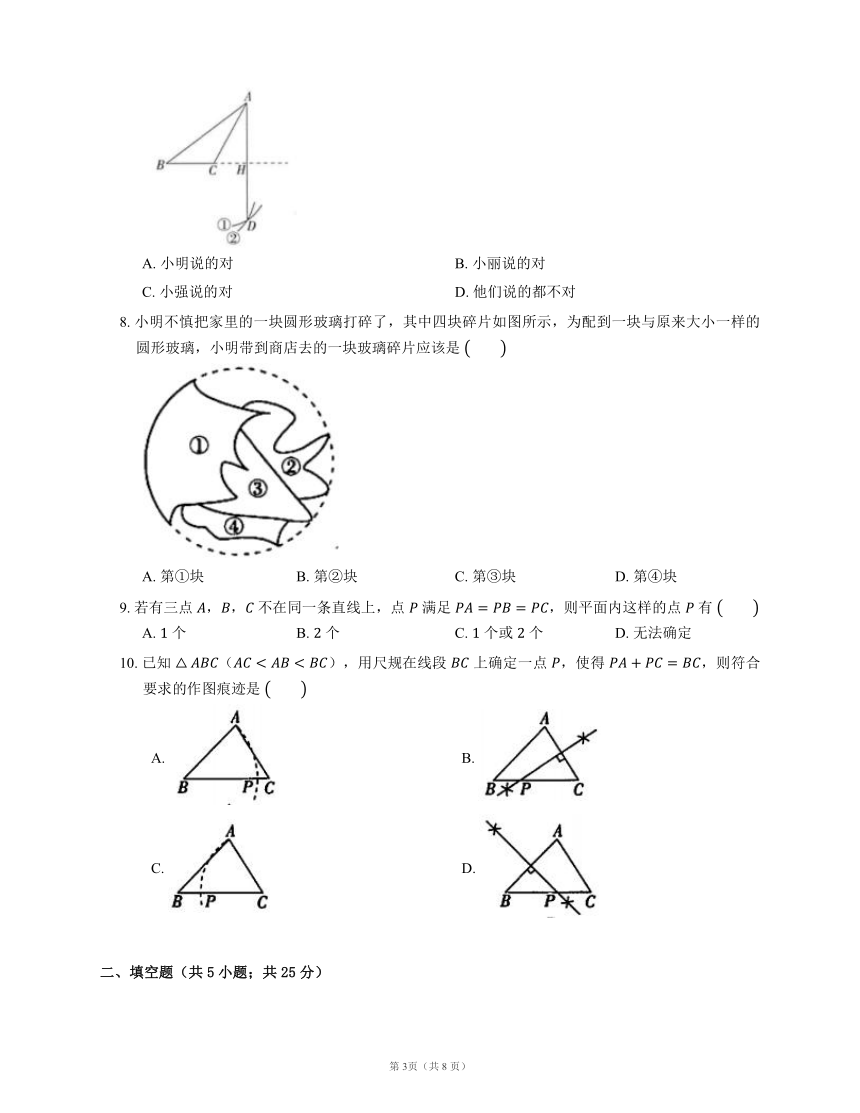
5. 如图所示的尺规作图是作
A. 线段的垂直平分线 B. 一个半径为定值的圆
C. 一条直线的平行线 D. 一个角等于已知角
6. 如图,在 中,线段 的垂直平分线与 相交于点 ,连接 ,边 的长为 ,边 的长为 ,则 的周长为
A. B. C. D.
7. 如图,已知钝角 ,老师按如下步骤尺规作图:
步骤 :以 为圆心, 的长为半径画弧①;
步骤 :以 为圆心, 的长为半径画弧②,交弧①于点 ;
步骤 :连接 ,交 延长线于点 .
小明说:图中的 且平分 .
小丽说:图中 平分 .
小强说:图中点 为 的中点.
你认为
A. 小明说的对 B. 小丽说的对
C. 小强说的对 D. 他们说的都不对
8. 小明不慎把家里的一块圆形玻璃打碎了,其中四块碎片如图所示,为配到一块与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是
A. 第①块 B. 第②块 C. 第③块 D. 第④块
9. 若有三点 ,, 不在同一条直线上,点 满足 ,则平面内这样的点 有
A. 个 B. 个 C. 个或 个 D. 无法确定
10. 已知 (),用尺规在线段 上确定一点 ,使得 ,则符合要求的作图痕迹是
A. B.
C. D.
二、填空题(共5小题;共25分)
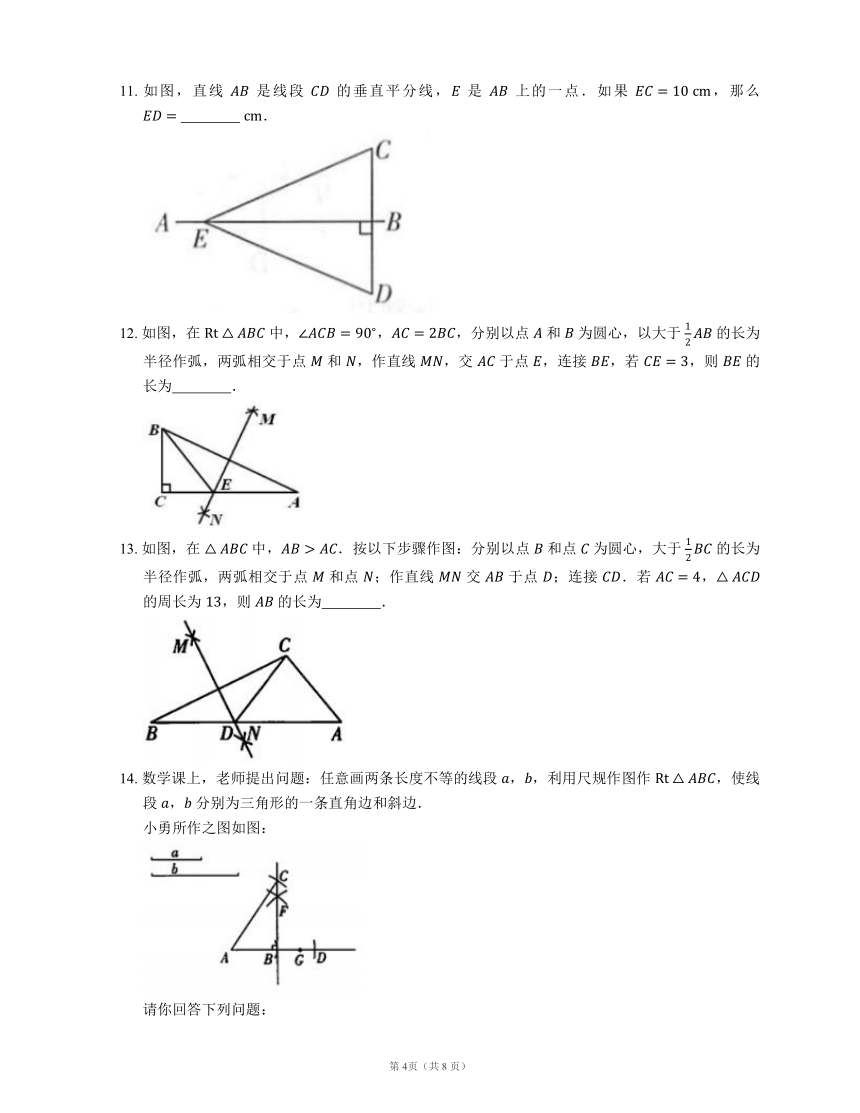
11. 如图,直线 是线段 的垂直平分线, 是 上的一点.如果 ,那么 .
12. 如图,在 中,,,分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ,作直线 ,交 于点 ,连接 ,若 ,则 的长为 .
13. 如图,在 中,.按以下步骤作图:分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 和点 ;作直线 交 于点 ;连接 .若 , 的周长为 ,则 的长为 .
14. 数学课上,老师提出问题:任意画两条长度不等的线段 ,,利用尺规作图作 ,使线段 , 分别为三角形的一条直角边和斜边.
小勇所作之图如图:
请你回答下列问题:
()在以下作图步骤中,小勇的作图顺序可能是 ;(只填序号)
①以 为圆心, 的长为半径画弧,交射线 于点 .
②画直线 .
③分别以点 , 为圆心,大于线段 的同样长为半径画弧,交于点 .
④以点 为圆心,线段 的长为半径画弧,交直线 于点 ,连接 .
⑤画射线 ,并在 上截取线段 .
() 的理由是 .
15. 如图,在 中, 的垂直平分线 分别交 , 于点 ,, 的垂直平分线 分别交 , 于点 ,,若 ,,则 的周长是 .
三、解答题(共3小题;共39分)
16. 如图,在 中,用尺规作图的方法作 边上的中线 .(不写作法,保留作图痕迹)
17. 如图,在四边形 中, 同时平分 和 .求证: 是 的垂直平分线.
18. 如图 中,边 的垂直平分线分别与 , 交于点 ,,如果 , 等于 度,求 的度数.
答案
第一部分
1. B
2. B
3. C
4. D
5. A
6. B 【解析】 线段 的垂直平分线与 相交于点 ,
,
的周长 ,
,,
的周长 .
7. A 【解析】如图,连接 ,,
,,
点 ,点 都在线段 的垂直平分线上,
直线 是线段 的垂直平分线,即 且平分 ,
故小明的说法正确;
而 不一定平分 ,故小丽的说法错误;
点 不一定为 的中点,故小强的说法错误.故选A.
8. A 【解析】要配到与原来大小一样的圆形玻璃,关键是确定圆的半径.小明带到商店去的一块玻璃碎片应该是第①块,可以在第①块碎片的圆弧上取两点,连接这两点得到一条弦,然后作这条弦的垂直平分线,同样,再作另一条弦的垂直平分线,两条垂直平分线的交点即为圆心,从而确定半径,该圆即可确定.
9. A 【解析】到点 , 距离相等的点在线段 的垂直平分线上,到点 , 距离相等的点在线段 的垂直平分线上,到点 , 距离相等的点在线段 的垂直平分线上,而三角形三边的垂直平分线交于一点.故选A.
10. D
【解析】由 ,可得 ,则点 在线段 的垂直平分线上.
第二部分
11.
12.
13.
14. ⑤①③②④,到线段两个端点距离相等的点在线段的垂直平分线上
15.
第三部分
16. 如图,
即为所求.
17. 同时平分 和 ,
,.
在 与 中,
().
,.
点 , 在 的垂直平分线上.
是 的垂直平分线.
18. 连接 ,
是线段 的垂直平分线,
,
,
,
,,
又 等于 度,
,
.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 通过如下尺规作图,能确定点 是 边中点的是
A. B.
C. D.
2. 如图,在 中, 的垂直平分线交 于点 ,交 于点 ,若 ,,则 的周长为
A. B. C. D.
3. 如图,,,则有
A. 与 互相垂直平分 B. 垂直平分
C. 垂直平分 D. 平分
4. 以下尺规作图中,一定能得到线段 的是
A. B.
C. D.
5. 如图所示的尺规作图是作
A. 线段的垂直平分线 B. 一个半径为定值的圆
C. 一条直线的平行线 D. 一个角等于已知角
6. 如图,在 中,线段 的垂直平分线与 相交于点 ,连接 ,边 的长为 ,边 的长为 ,则 的周长为
A. B. C. D.
7. 如图,已知钝角 ,老师按如下步骤尺规作图:
步骤 :以 为圆心, 的长为半径画弧①;
步骤 :以 为圆心, 的长为半径画弧②,交弧①于点 ;
步骤 :连接 ,交 延长线于点 .
小明说:图中的 且平分 .
小丽说:图中 平分 .
小强说:图中点 为 的中点.
你认为
A. 小明说的对 B. 小丽说的对
C. 小强说的对 D. 他们说的都不对
8. 小明不慎把家里的一块圆形玻璃打碎了,其中四块碎片如图所示,为配到一块与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是
A. 第①块 B. 第②块 C. 第③块 D. 第④块
9. 若有三点 ,, 不在同一条直线上,点 满足 ,则平面内这样的点 有
A. 个 B. 个 C. 个或 个 D. 无法确定
10. 已知 (),用尺规在线段 上确定一点 ,使得 ,则符合要求的作图痕迹是
A. B.
C. D.
二、填空题(共5小题;共25分)
11. 如图,直线 是线段 的垂直平分线, 是 上的一点.如果 ,那么 .
12. 如图,在 中,,,分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ,作直线 ,交 于点 ,连接 ,若 ,则 的长为 .
13. 如图,在 中,.按以下步骤作图:分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 和点 ;作直线 交 于点 ;连接 .若 , 的周长为 ,则 的长为 .
14. 数学课上,老师提出问题:任意画两条长度不等的线段 ,,利用尺规作图作 ,使线段 , 分别为三角形的一条直角边和斜边.
小勇所作之图如图:
请你回答下列问题:
()在以下作图步骤中,小勇的作图顺序可能是 ;(只填序号)
①以 为圆心, 的长为半径画弧,交射线 于点 .
②画直线 .
③分别以点 , 为圆心,大于线段 的同样长为半径画弧,交于点 .
④以点 为圆心,线段 的长为半径画弧,交直线 于点 ,连接 .
⑤画射线 ,并在 上截取线段 .
() 的理由是 .
15. 如图,在 中, 的垂直平分线 分别交 , 于点 ,, 的垂直平分线 分别交 , 于点 ,,若 ,,则 的周长是 .
三、解答题(共3小题;共39分)
16. 如图,在 中,用尺规作图的方法作 边上的中线 .(不写作法,保留作图痕迹)
17. 如图,在四边形 中, 同时平分 和 .求证: 是 的垂直平分线.
18. 如图 中,边 的垂直平分线分别与 , 交于点 ,,如果 , 等于 度,求 的度数.
答案
第一部分
1. B
2. B
3. C
4. D
5. A
6. B 【解析】 线段 的垂直平分线与 相交于点 ,
,
的周长 ,
,,
的周长 .
7. A 【解析】如图,连接 ,,
,,
点 ,点 都在线段 的垂直平分线上,
直线 是线段 的垂直平分线,即 且平分 ,
故小明的说法正确;
而 不一定平分 ,故小丽的说法错误;
点 不一定为 的中点,故小强的说法错误.故选A.
8. A 【解析】要配到与原来大小一样的圆形玻璃,关键是确定圆的半径.小明带到商店去的一块玻璃碎片应该是第①块,可以在第①块碎片的圆弧上取两点,连接这两点得到一条弦,然后作这条弦的垂直平分线,同样,再作另一条弦的垂直平分线,两条垂直平分线的交点即为圆心,从而确定半径,该圆即可确定.
9. A 【解析】到点 , 距离相等的点在线段 的垂直平分线上,到点 , 距离相等的点在线段 的垂直平分线上,到点 , 距离相等的点在线段 的垂直平分线上,而三角形三边的垂直平分线交于一点.故选A.
10. D
【解析】由 ,可得 ,则点 在线段 的垂直平分线上.
第二部分
11.
12.
13.
14. ⑤①③②④,到线段两个端点距离相等的点在线段的垂直平分线上
15.
第三部分
16. 如图,
即为所求.
17. 同时平分 和 ,
,.
在 与 中,
().
,.
点 , 在 的垂直平分线上.
是 的垂直平分线.
18. 连接 ,
是线段 的垂直平分线,
,
,
,
,,
又 等于 度,
,
.
第1页(共1 页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
