2021-2022学年高二上学期数学人教A版必修5 2.4等比数列 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版必修5 2.4等比数列 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 11:59:22 | ||
图片预览








文档简介
(共24张PPT)
2.4 等 比 数 列
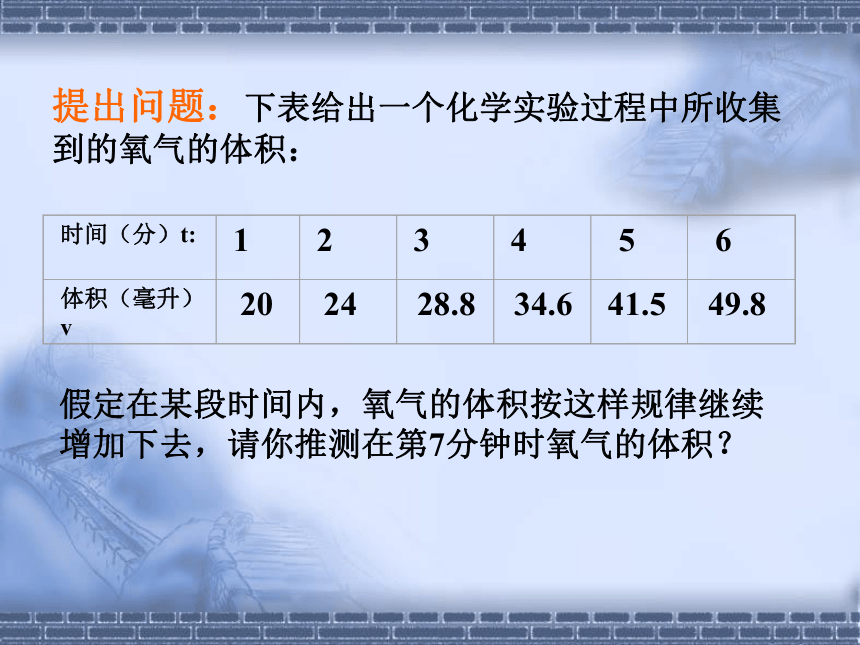
提出问题:下表给出一个化学实验过程中所收集
到的氧气的体积:
时间(分)t:
1
2
3
4
5
6
体积(毫升)v
20
24
28.8
34.6
41.5
49.8
假定在某段时间内,氧气的体积按这样规律继续
增加下去,请你推测在第7分钟时氧气的体积?
研究1 估算
为了提高科学性和准确性,
28.8
4
6
t分钟
1
20
24
34.4
41.5
49.8
V毫升
2
3
5
从图像大致可以看出,以上述数据所描的点在一条
指数函数型的图像上。
研究2 函数拟合
研究3 由于在整分钟时测得的氧气体积数值组成
的数列{ vt },因此我们还可以从数列的角度来分析,
寻求数据之间的规律性。
20,24,28.8,34.6,41.5,49.8,…,vn.
时间(分)t:
1
2
3
4
5
6
体积(毫升)v
20
24
28.8
34.6
41.5
49.8
即
由此可知每个整分钟时的体积与它前一整分钟时的体积的比(保留两位有效数字)是一个常数.
即
即:从第二项起,该数列的后一项与其前一项的比
是同一个常数1.2.
由此我们发现由氧气体积数值所组成的数列{ vt }有这样一个规律,
我们将具有这样特点的数列叫等比数列,
其中常数1.2叫公比。
因此,我们可以推测:第7分钟时氧气的体积
v7 = v6×1.2=49.8×1.2=59.76
该公式叫等比数列{ vt }的通项公式,它表示这个
数列的第t项数值与项数t之间的一种指数型函数
关系,图像如图所示。
研究4 假定在某段时间内,按照这样的规律继续增加下去,那么如何探究这个体积的一般公式呢?
从上面我们看到:
v2 = v1×1.2=20×1.2;
v3 = v2×1.2=v1×1.22=20×1.22 ;
v4 = v3×1.2=v1×1.23=20×1.23;
……
因此得到表示第t分钟时的体积公式vt=20×1.2t -1。
28.8
4
6
t分钟
1
20
24
34.4
41.5
49.8
V毫升
2
3
5
研究5 由以上实例,一般地,如何给出等比数列
{an}的定义和通项公式呢?
1.(1)等比数列的定义是什么?
等比数列的定义:
如果一个数列从第2项起,每一项与它的前一项
的比都等于同一个常数,那么这个数列就叫做等
比数列,这个常数叫做等比数列的公比,公比通
常用 q表示.
(2)用递推式如何表达?
(q≠0 )
2.下列数列是否是等比数列?如果是,
公比q是多少?
等比数列:
如果一个数列从第2项起,
每一项与它的前一项
的比都等于同一个常数。
一、等比数列的定义
3.(1)等比数列的通项公式是什么?
等比数列的通项公式:
一般地,若等比数列{an}的公比为q,
则通项公式为:an=a1·qn-1 。
(2)等比数列的通项公式是如何得到的?
根据等比数列的定义:从第二项起每一项都等于它的前一项乘以公比 q ,所以
由此得到:
所以它即为等比数列通项公式
其中,a1与q均不为0.且当n=1时也成立.
分析2:根据等比数列的定义:
其中,a1与q均不为0.且当n=1时也成立.
等比数列的定义式:
等比数列的通项公式:
思考:
(3)等比数列的通项公式与所学的哪类函数相近?
三、等比中项
四、等比数列判定方法
三、等比中项
五、等比数列的性质
等差数列的性质
小结:
2. 练习2、3做书上.
3. 习题3、5、6做作业本上.
1.阅读教材 例1、例2,并思考
例1、例2在应用通项公式时,反映了
什么思想方法?
例2的方程如何解出?
练习及作业:
2.4 等 比 数 列
提出问题:下表给出一个化学实验过程中所收集
到的氧气的体积:
时间(分)t:
1
2
3
4
5
6
体积(毫升)v
20
24
28.8
34.6
41.5
49.8
假定在某段时间内,氧气的体积按这样规律继续
增加下去,请你推测在第7分钟时氧气的体积?
研究1 估算
为了提高科学性和准确性,
28.8
4
6
t分钟
1
20
24
34.4
41.5
49.8
V毫升
2
3
5
从图像大致可以看出,以上述数据所描的点在一条
指数函数型的图像上。
研究2 函数拟合
研究3 由于在整分钟时测得的氧气体积数值组成
的数列{ vt },因此我们还可以从数列的角度来分析,
寻求数据之间的规律性。
20,24,28.8,34.6,41.5,49.8,…,vn.
时间(分)t:
1
2
3
4
5
6
体积(毫升)v
20
24
28.8
34.6
41.5
49.8
即
由此可知每个整分钟时的体积与它前一整分钟时的体积的比(保留两位有效数字)是一个常数.
即
即:从第二项起,该数列的后一项与其前一项的比
是同一个常数1.2.
由此我们发现由氧气体积数值所组成的数列{ vt }有这样一个规律,
我们将具有这样特点的数列叫等比数列,
其中常数1.2叫公比。
因此,我们可以推测:第7分钟时氧气的体积
v7 = v6×1.2=49.8×1.2=59.76
该公式叫等比数列{ vt }的通项公式,它表示这个
数列的第t项数值与项数t之间的一种指数型函数
关系,图像如图所示。
研究4 假定在某段时间内,按照这样的规律继续增加下去,那么如何探究这个体积的一般公式呢?
从上面我们看到:
v2 = v1×1.2=20×1.2;
v3 = v2×1.2=v1×1.22=20×1.22 ;
v4 = v3×1.2=v1×1.23=20×1.23;
……
因此得到表示第t分钟时的体积公式vt=20×1.2t -1。
28.8
4
6
t分钟
1
20
24
34.4
41.5
49.8
V毫升
2
3
5
研究5 由以上实例,一般地,如何给出等比数列
{an}的定义和通项公式呢?
1.(1)等比数列的定义是什么?
等比数列的定义:
如果一个数列从第2项起,每一项与它的前一项
的比都等于同一个常数,那么这个数列就叫做等
比数列,这个常数叫做等比数列的公比,公比通
常用 q表示.
(2)用递推式如何表达?
(q≠0 )
2.下列数列是否是等比数列?如果是,
公比q是多少?
等比数列:
如果一个数列从第2项起,
每一项与它的前一项
的比都等于同一个常数。
一、等比数列的定义
3.(1)等比数列的通项公式是什么?
等比数列的通项公式:
一般地,若等比数列{an}的公比为q,
则通项公式为:an=a1·qn-1 。
(2)等比数列的通项公式是如何得到的?
根据等比数列的定义:从第二项起每一项都等于它的前一项乘以公比 q ,所以
由此得到:
所以它即为等比数列通项公式
其中,a1与q均不为0.且当n=1时也成立.
分析2:根据等比数列的定义:
其中,a1与q均不为0.且当n=1时也成立.
等比数列的定义式:
等比数列的通项公式:
思考:
(3)等比数列的通项公式与所学的哪类函数相近?
三、等比中项
四、等比数列判定方法
三、等比中项
五、等比数列的性质
等差数列的性质
小结:
2. 练习2、3做书上.
3. 习题3、5、6做作业本上.
1.阅读教材 例1、例2,并思考
例1、例2在应用通项公式时,反映了
什么思想方法?
例2的方程如何解出?
练习及作业:
