2021-2022学年高二上学期数学人教A版必修5 2.1数列的概念 课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版必修5 2.1数列的概念 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 909.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 12:00:29 | ||
图片预览







文档简介
(共25张PPT)
数 列
sequence of number
背景:
1. 古希腊毕达哥拉斯学派在公元前研究过:
(1)1,3,6,10,… (三角形数)
(2)1,4,9,16,… (正方形数)
2. 国际象棋的故事:
传说:
古印度国王要奖励国际象棋的发明者,问他有什么要求,发明者说:“请在第一个格子里放上1粒麦子,在第二个格子里放上2粒麦子,在第三个格子里放上 4粒麦子,在第四个格子里放上8粒麦子,依此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子。请给我足够的粮食来实现上述要求”。国王觉得太容易了,就同意了他的要求。
你觉得国王能办到吗
1
2
22
23
24
25
26
27
…
263
你想得到
什么样的
赏赐?
陛下赏小
人几粒麦就
搞定。
OK
陛下国库里的麦子不够小人搬啊!
1
2
4
8
…
263
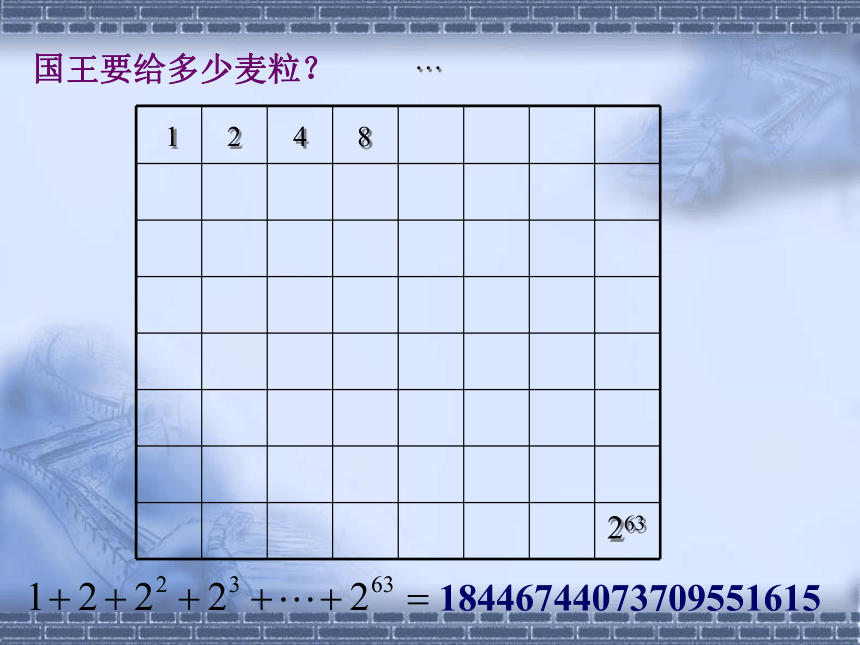
国王要给多少麦粒?
18446744073709551615
3. 斐波那契和他的《算盘书》(13世纪)
兔子问题:
假设一对兔子成配偶后,在两个月时可以生下一对
(一雌一雄)兔子。以后,每过足一个月可以生下
另一对兔子。如果每只兔子都能健康存活,一年之
后,会有多少对兔子呢?
斐波那契数列:
1,1,2,3,5,8,13,21,…
按一定的次序排列的一列数叫做数列
数列中的每一个数都叫做这个数列的项
放射性物质衰减后的剩余量.
平均增长率问题中每年的产量(利息等);
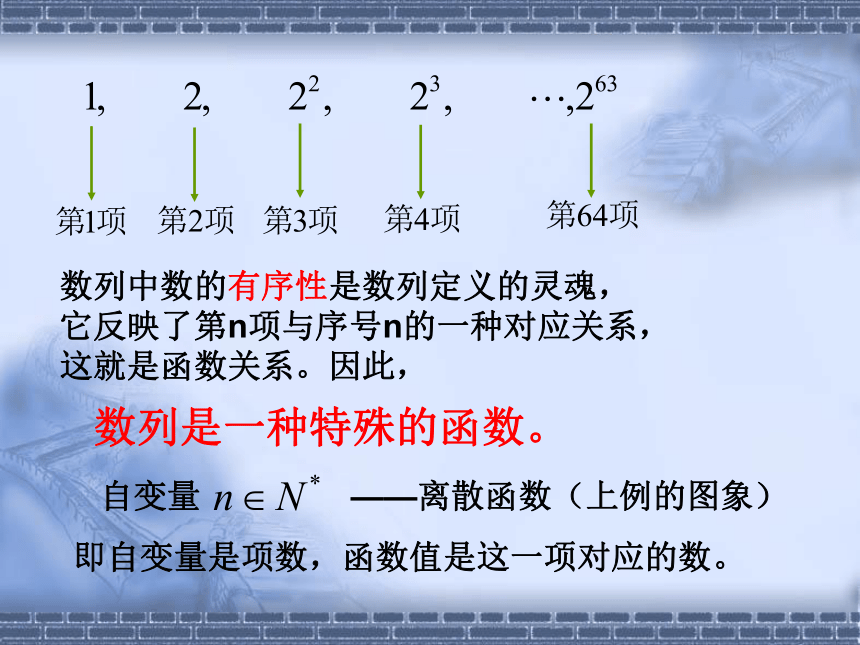
数列中数的有序性是数列定义的灵魂,
它反映了第n项与序号n的一种对应关系,
这就是函数关系。因此,
数列是一种特殊的函数。
自变量
即自变量是项数,函数值是这一项对应的数。
——离散函数(上例的图象)
定义域为正整数集(或其有限子集)的函数
1 2 3 4
此函数(数列)的图象是什么?
y=f(x)
an
n
函数值
自变量
?
数列 图象
O 1 2 3 4 5 6 7
10
9
8
7
6
5
4
3
2
1
数列图象是一群孤立
的点(离散).
——函数解析式
(离散函数)
项数有限的数列叫做有穷数列;
记作
项数无限的数列叫做无穷数列;
记作
数列一般记作
(2)数列按项与项之间的大小关系
分为:
如果已知数列 的第1项(或前几项),且任一项 与它的前一项 (或前几项)间的关系可用一个公式表达,这个公式叫数列的
递推公式。
例3:已知数列 的首项为1,
以后各项由公式
给出,写出该数列前5项
解:
例4:已知 数列 1,1,2,3,5,8,13,
21,34,··· ,请写出它的一个递推公式 .
解:
观察数列的前 n 项,有:
a1=a2=1
a3= 2 =1+1= a1+a2
a4= 3 =1+2= a2+a3
a5= 5 =2+3= a3+a4
···
所以 an= an-2+an-1 (n≥3) 为所求递推公式
三 小结:
1.知识结构图:
数列
数列概念
数列表示法
数列分类
列举法
图象法
通项公式
递推公式
三 小结:
2 应用:
(1)由通项公式求数列各项。 (2)由数列各项写出通项公式。
(3)由递推公式写出数列各项。
1.知识结构图:
作业:
1.书练习做书上.
2.习题 1——4(作业本).
数 列
sequence of number
背景:
1. 古希腊毕达哥拉斯学派在公元前研究过:
(1)1,3,6,10,… (三角形数)
(2)1,4,9,16,… (正方形数)
2. 国际象棋的故事:
传说:
古印度国王要奖励国际象棋的发明者,问他有什么要求,发明者说:“请在第一个格子里放上1粒麦子,在第二个格子里放上2粒麦子,在第三个格子里放上 4粒麦子,在第四个格子里放上8粒麦子,依此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子。请给我足够的粮食来实现上述要求”。国王觉得太容易了,就同意了他的要求。
你觉得国王能办到吗
1
2
22
23
24
25
26
27
…
263
你想得到
什么样的
赏赐?
陛下赏小
人几粒麦就
搞定。
OK
陛下国库里的麦子不够小人搬啊!
1
2
4
8
…
263
国王要给多少麦粒?
18446744073709551615
3. 斐波那契和他的《算盘书》(13世纪)
兔子问题:
假设一对兔子成配偶后,在两个月时可以生下一对
(一雌一雄)兔子。以后,每过足一个月可以生下
另一对兔子。如果每只兔子都能健康存活,一年之
后,会有多少对兔子呢?
斐波那契数列:
1,1,2,3,5,8,13,21,…
按一定的次序排列的一列数叫做数列
数列中的每一个数都叫做这个数列的项
放射性物质衰减后的剩余量.
平均增长率问题中每年的产量(利息等);
数列中数的有序性是数列定义的灵魂,
它反映了第n项与序号n的一种对应关系,
这就是函数关系。因此,
数列是一种特殊的函数。
自变量
即自变量是项数,函数值是这一项对应的数。
——离散函数(上例的图象)
定义域为正整数集(或其有限子集)的函数
1 2 3 4
此函数(数列)的图象是什么?
y=f(x)
an
n
函数值
自变量
?
数列 图象
O 1 2 3 4 5 6 7
10
9
8
7
6
5
4
3
2
1
数列图象是一群孤立
的点(离散).
——函数解析式
(离散函数)
项数有限的数列叫做有穷数列;
记作
项数无限的数列叫做无穷数列;
记作
数列一般记作
(2)数列按项与项之间的大小关系
分为:
如果已知数列 的第1项(或前几项),且任一项 与它的前一项 (或前几项)间的关系可用一个公式表达,这个公式叫数列的
递推公式。
例3:已知数列 的首项为1,
以后各项由公式
给出,写出该数列前5项
解:
例4:已知 数列 1,1,2,3,5,8,13,
21,34,··· ,请写出它的一个递推公式 .
解:
观察数列的前 n 项,有:
a1=a2=1
a3= 2 =1+1= a1+a2
a4= 3 =1+2= a2+a3
a5= 5 =2+3= a3+a4
···
所以 an= an-2+an-1 (n≥3) 为所求递推公式
三 小结:
1.知识结构图:
数列
数列概念
数列表示法
数列分类
列举法
图象法
通项公式
递推公式
三 小结:
2 应用:
(1)由通项公式求数列各项。 (2)由数列各项写出通项公式。
(3)由递推公式写出数列各项。
1.知识结构图:
作业:
1.书练习做书上.
2.习题 1——4(作业本).
