第一章轴对称与轴对称图形复习课

主备人： 把关人： 研讨成员：初二数学组
教案序号
课时
1
课型
复习课
课 题
第一章：轴对称与轴对称图形
重点、难点
重点: 轴对称图形的性质，以及运用于解题
难点: 有条理地表达，熟练地运用已知结论解决问题
教学目标
回顾本章所学知识，查漏补缺
2、运用诸性质解题，体会几何证明的思想，学会清晰、有条理地表达思想
教学
准备
无
教学过程
教学环节
教材处理
师生
活动
二次备课
一复习基础知识
二基础巩固
三综合提升
四小结
五作业
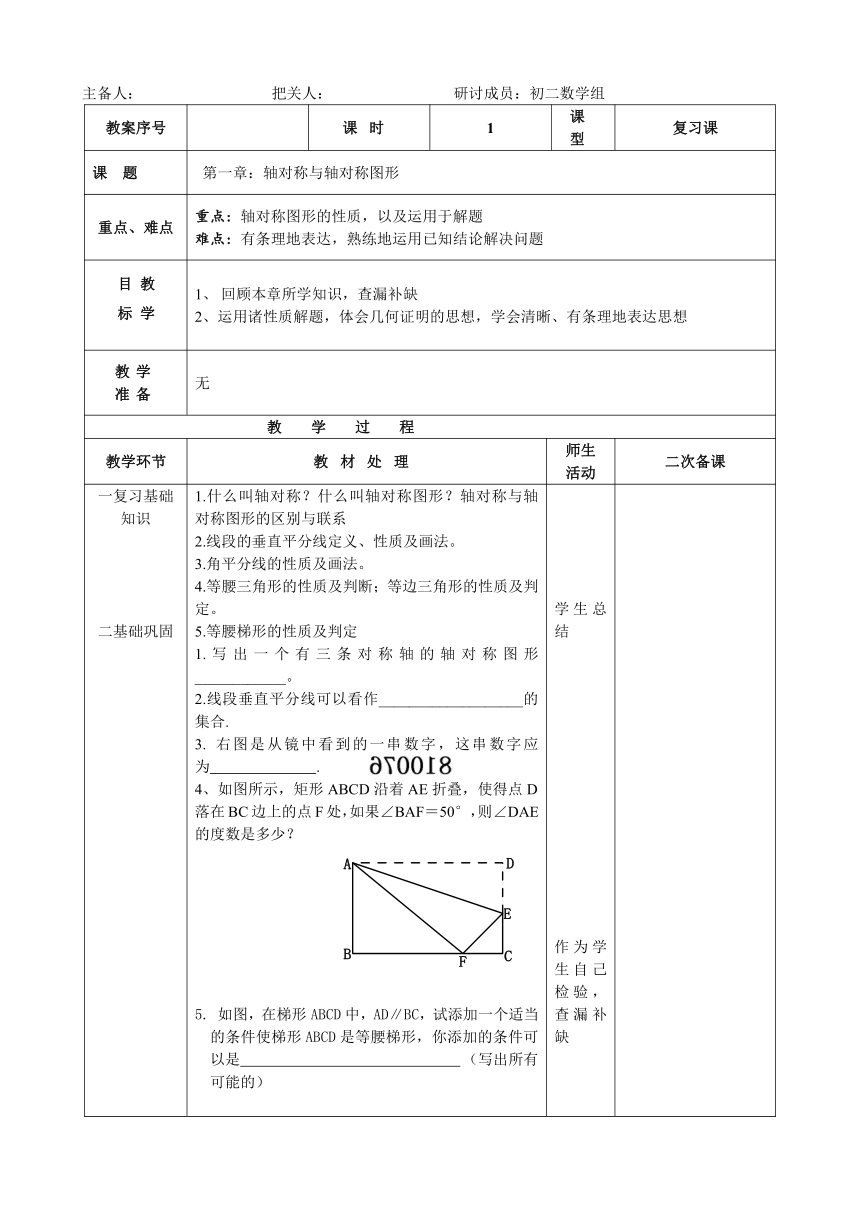
1.什么叫轴对称？什么叫轴对称图形？轴对称与轴对称图形的区别与联系2.线段的垂直平分线定义、性质及画法。3.角平分线的性质及画法。4.等腰三角形的性质及判断；等边三角形的性质及判定。5.等腰梯形的性质及判定
1.写出一个有三条对称轴的轴对称图形____________。
2.线段垂直平分线可以看作___________________的集合.
3. 右图是从镜中看到的一串数字，这串数字应为 .
4、如图所示，矩形ABCD沿着AE折叠，使得点D落在BC边上的点F处，如果∠BAF＝50°，则∠DAE的度数是多少？
5. 如图，在梯形ABCD中，AD∥BC，试添加一个适当的条件使梯形ABCD是等腰梯形，你添加的条件可以是 （写出所有可能的）
6. 等腰三角形底边上的高是底边的一半，则其顶角的大小为___________．
7.如图，在△ABC中，∠B＝90°，∠A＝36°，AC的垂直平分线MN与AB交于点D，则∠BCD的度数是____________。
8.如图，△ABC中，∠B＝80°，AC边的垂直平分线DE与AB交于点D，与AC交于点E，且∠ACD∶∠BCD＝2：1，则∠ACB＝______.
9、墙上钉了一根木条，小明想检验这根木条是否水平，他拿来一个如图所示的测平仪，在这个测平仪中，AB＝AC，BC边的中点D处挂了一个重锤。小明将BC边与木条重合，观察此时重锤是否通过A点，那么这根木条是水平的，这是因为_______________________________
10、如图，∠A＝15°，AB＝BC＝CD＝DE＝EF，则∠DEF等于_________
*11、在正三角形ABC所在的平面上找一点P，使得△PAB、△PBC、△PAC都是等腰三角形。这样的P点能找到几个？
1、如图，直线l是一条河，P、Q两地相距8千米，P、Q两地到l的距离分别为2千米、5千米，欲在l上的某点M处修建一个水泵站，向P、Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则铺设的管道最短的是（ ）．
2、（选做）如图，AB＝AC＝BD，求证：3∠1－∠2＝180°
本节的知识梳理
课本30页检测站
学生总结
作为学生自己检验，查漏补缺
提高学生的知识层面
板书设计
第一章：轴对称与轴对称图形
本章的知识梳理：
教学反思