人教版九年级数学上册24.1.1圆课件(共17张ppt)
文档属性
| 名称 | 人教版九年级数学上册24.1.1圆课件(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 907.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-15 21:04:09 | ||
图片预览


文档简介
(共17张PPT)
圆是生活中常见的图形,许多物体都给我们以圆的形象
引入、感知圆的世界
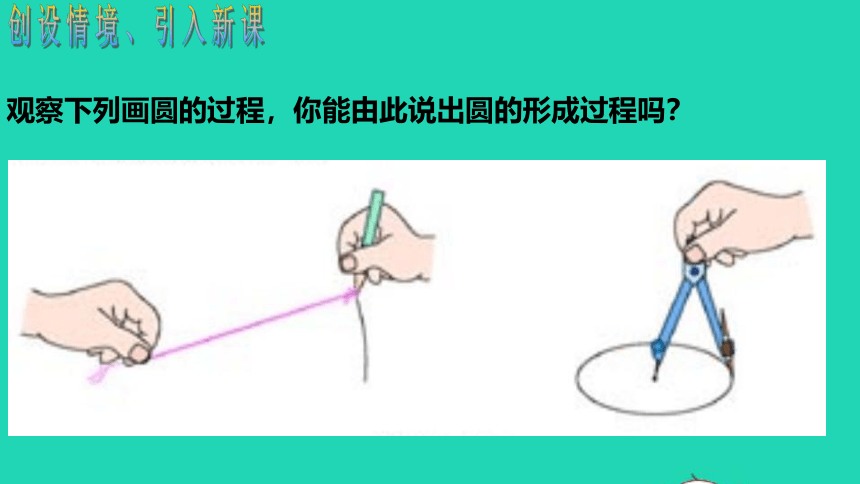
观察下列画圆的过程,你能由此说出圆的形成过程吗?
创设情境、引入新课
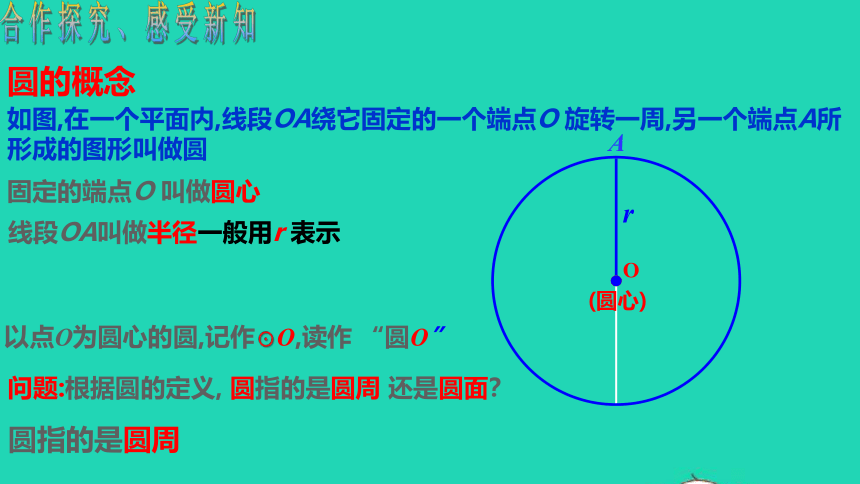
如图,在一个平面内,线段OA绕它固定的一个端点O 旋转一周,另一个端点A所形成的图形叫做圆
·
O
A
固定的端点O 叫做圆心
线段OA叫做半径一般用r 表示
以点O为圆心的圆,记作⊙O,读作 “圆O”
圆的概念
问题:根据圆的定义, 圆指的是圆周 还是圆面?
圆指的是圆周
合作探究、感受新知
r
(圆心)
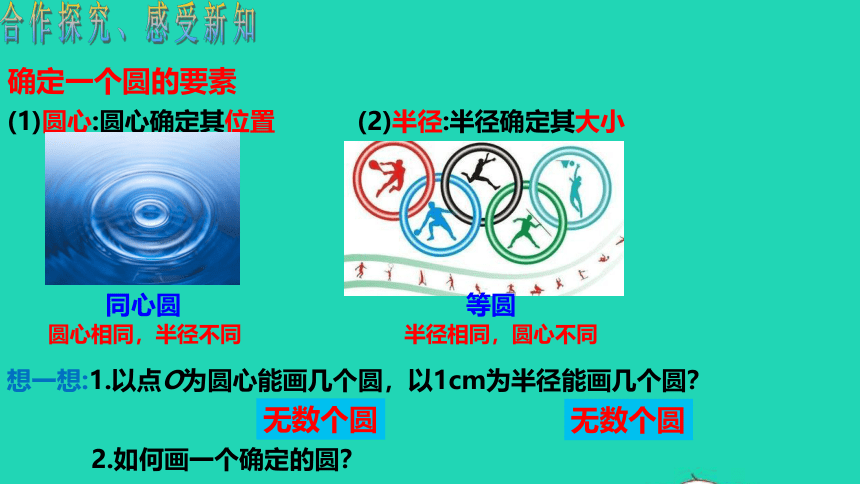
(1)圆心:圆心确定其位置 (2)半径:半径确定其大小
同心圆
圆心相同,半径不同
想一想:1.以点O为圆心能画几个圆,以1cm为半径能画几个圆?
无数个圆
无数个圆
确定一个圆的要素
2.如何画一个确定的圆?
合作探究、感受新知
半径相同,圆心不同
等圆
归纳:圆心为O、半径为r 的圆可以看成是所有到定点O 的距离都等于定长r 的所有点的集合.
从画圆的过程可以看出:
(1)圆上各点到定点(圆心O )的距离都等于定长(半径r)
(2)到定点的距离等于定长的点都在同一个圆上
合作探究、感受新知
动态:在一个平面内,线段OA绕它固定的一个端点O 旋转一周,另一个端
点A所形成的图形叫做圆.
静态:圆心为O、半径为r 的圆可以看成是所有到定点O 的距离等于定长r
的点组成的图形.
圆的两种定义
·
r
O
A
A
B
C
D
O
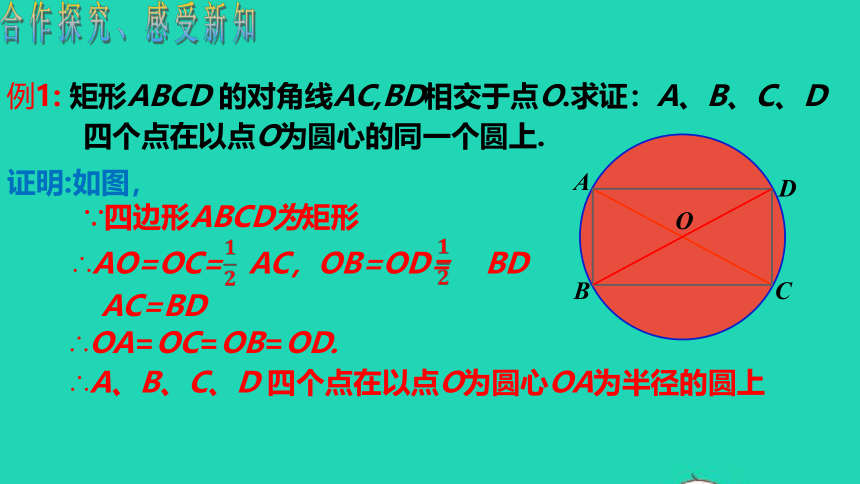
证明:如图,
∵四边形ABCD为矩形
∴OA=OC=OB=OD.
∴A、B、C、D 四个点在以点O为圆心OA为半径的圆上
例1: 矩形ABCD 的对角线AC,BD相交于点O.求证:A、B、C、D
四个点在以点O为圆心的同一个圆上.
合作探究、感受新知
∴AO=OC= AC,OB=OD= BD
AC=BD
经过圆心的弦(如图中的AB )叫做直径
·
C
O
A
B
连接圆上任意两点的线段(如图AC )叫做弦
与圆有关的概念
弦
合作探究、感受新知
注意: 1.弦和直径都是线段
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定
是直径
圆的任意一条直径的两个端点把圆分成两
条弧,每一条弧都叫做半圆.
圆上任意两点间的部分叫做圆弧,简称弧.
以A,B为端点的弧
记作 ,读作“圆弧AB”或“弧AB”.
⌒
AB
C
A
合作探究、感受新知
弧
O
B
N
M
⌒
MN
( 叫做半圆)
·
C
O
A
B
小于半圆的弧叫做劣弧,如图中的AC
(
大于半圆的弧(用三个点表示)叫做优弧,如图中的ABC
(
劣弧与优弧
合作探究、感受新知
弧有三类:分别是优弧、劣弧、半圆
由弦及其所对的弧组成的图形叫弓形.图中弦AC,弧AC组成的图形叫做弓形AC
·
B
O
A
等圆:能够重合的两个圆
·
O1
等弧:在同圆或等圆中,能够互相重合的弧
合作探究、感受新知
等圆与等弧
容易看出:半径相等的两个圆是等圆
反过来,同圆或等圆的半径相等
·
A′
B′
⌒
AB
⌒
A′B′
与 是等弧
思考:长度相等的弧是等弧吗?
不一定没有重合
(1)请写出以点A为端点的劣弧及优弧;
(2)请写出以点A为端点的弦及直径;
弦AB、AF、AD 其中弦AD又是直径
(3)请任选一条弦,写出这条弦所对的弧.
弦AF,它所对的弧是
O
劣弧:
AB,
(
ABE,
(
新知运用、提升能力
F
E
D
C
B
A
AE,
(
AF,
(
AC,
(
ABF,
(
AFC,
(
AFB,
(
优弧:
AF,
(
ABF,
(
例2 如图
(答案不唯一)
1.平面上的一点和⊙O上的最近点距离为2cm,最远点距离为8cm,则圆O
的半径是_____________ .
5cm或3cm
新知运用、提升能力
练习:
2.判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
3. 一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.
5m
参考答案:
新知运用、提升能力
5m
O
4m
1.如何在操场上画一个半径是5m的圆?说出你的理由.
教材P81 练习
巩固练习、反馈效果
确定圆心 半径(5米长绳)
2.你见过树木的年轮吗 从树木的年轮,可以知道树木的年龄.把树木的横截面看成是圆形的,如果一棵20年树龄的树干直径是23cm,这棵树的半径平均每年增加多少 .
解: 23÷2÷20=0.575cm
∴这棵红衫树的半径每年增加0.575cm
3.如图,△ABC中,∠C=900.求证:A,B,C三点在同一个圆上.
巩固练习、反馈效果
教材P81 练习
·
C
B
A
证明:如图,取AB的中点O并连接OC
O
小结回顾、梳理新知
通过这节课的学习,我们认识了很多新的知识,说一说你自己有什么收获呢?
1.理解并掌握圆的两种定义;
静态定义 动态定义
2.理解圆有关的概念:
同心圆(等圆)
弦:(直径)
弧:(半圆、优弧、劣弧)等弧
圆是生活中常见的图形,许多物体都给我们以圆的形象
引入、感知圆的世界
观察下列画圆的过程,你能由此说出圆的形成过程吗?
创设情境、引入新课
如图,在一个平面内,线段OA绕它固定的一个端点O 旋转一周,另一个端点A所形成的图形叫做圆
·
O
A
固定的端点O 叫做圆心
线段OA叫做半径一般用r 表示
以点O为圆心的圆,记作⊙O,读作 “圆O”
圆的概念
问题:根据圆的定义, 圆指的是圆周 还是圆面?
圆指的是圆周
合作探究、感受新知
r
(圆心)
(1)圆心:圆心确定其位置 (2)半径:半径确定其大小
同心圆
圆心相同,半径不同
想一想:1.以点O为圆心能画几个圆,以1cm为半径能画几个圆?
无数个圆
无数个圆
确定一个圆的要素
2.如何画一个确定的圆?
合作探究、感受新知
半径相同,圆心不同
等圆
归纳:圆心为O、半径为r 的圆可以看成是所有到定点O 的距离都等于定长r 的所有点的集合.
从画圆的过程可以看出:
(1)圆上各点到定点(圆心O )的距离都等于定长(半径r)
(2)到定点的距离等于定长的点都在同一个圆上
合作探究、感受新知
动态:在一个平面内,线段OA绕它固定的一个端点O 旋转一周,另一个端
点A所形成的图形叫做圆.
静态:圆心为O、半径为r 的圆可以看成是所有到定点O 的距离等于定长r
的点组成的图形.
圆的两种定义
·
r
O
A
A
B
C
D
O
证明:如图,
∵四边形ABCD为矩形
∴OA=OC=OB=OD.
∴A、B、C、D 四个点在以点O为圆心OA为半径的圆上
例1: 矩形ABCD 的对角线AC,BD相交于点O.求证:A、B、C、D
四个点在以点O为圆心的同一个圆上.
合作探究、感受新知
∴AO=OC= AC,OB=OD= BD
AC=BD
经过圆心的弦(如图中的AB )叫做直径
·
C
O
A
B
连接圆上任意两点的线段(如图AC )叫做弦
与圆有关的概念
弦
合作探究、感受新知
注意: 1.弦和直径都是线段
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定
是直径
圆的任意一条直径的两个端点把圆分成两
条弧,每一条弧都叫做半圆.
圆上任意两点间的部分叫做圆弧,简称弧.
以A,B为端点的弧
记作 ,读作“圆弧AB”或“弧AB”.
⌒
AB
C
A
合作探究、感受新知
弧
O
B
N
M
⌒
MN
( 叫做半圆)
·
C
O
A
B
小于半圆的弧叫做劣弧,如图中的AC
(
大于半圆的弧(用三个点表示)叫做优弧,如图中的ABC
(
劣弧与优弧
合作探究、感受新知
弧有三类:分别是优弧、劣弧、半圆
由弦及其所对的弧组成的图形叫弓形.图中弦AC,弧AC组成的图形叫做弓形AC
·
B
O
A
等圆:能够重合的两个圆
·
O1
等弧:在同圆或等圆中,能够互相重合的弧
合作探究、感受新知
等圆与等弧
容易看出:半径相等的两个圆是等圆
反过来,同圆或等圆的半径相等
·
A′
B′
⌒
AB
⌒
A′B′
与 是等弧
思考:长度相等的弧是等弧吗?
不一定没有重合
(1)请写出以点A为端点的劣弧及优弧;
(2)请写出以点A为端点的弦及直径;
弦AB、AF、AD 其中弦AD又是直径
(3)请任选一条弦,写出这条弦所对的弧.
弦AF,它所对的弧是
O
劣弧:
AB,
(
ABE,
(
新知运用、提升能力
F
E
D
C
B
A
AE,
(
AF,
(
AC,
(
ABF,
(
AFC,
(
AFB,
(
优弧:
AF,
(
ABF,
(
例2 如图
(答案不唯一)
1.平面上的一点和⊙O上的最近点距离为2cm,最远点距离为8cm,则圆O
的半径是_____________ .
5cm或3cm
新知运用、提升能力
练习:
2.判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
3. 一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.
5m
参考答案:
新知运用、提升能力
5m
O
4m
1.如何在操场上画一个半径是5m的圆?说出你的理由.
教材P81 练习
巩固练习、反馈效果
确定圆心 半径(5米长绳)
2.你见过树木的年轮吗 从树木的年轮,可以知道树木的年龄.把树木的横截面看成是圆形的,如果一棵20年树龄的树干直径是23cm,这棵树的半径平均每年增加多少 .
解: 23÷2÷20=0.575cm
∴这棵红衫树的半径每年增加0.575cm
3.如图,△ABC中,∠C=900.求证:A,B,C三点在同一个圆上.
巩固练习、反馈效果
教材P81 练习
·
C
B
A
证明:如图,取AB的中点O并连接OC
O
小结回顾、梳理新知
通过这节课的学习,我们认识了很多新的知识,说一说你自己有什么收获呢?
1.理解并掌握圆的两种定义;
静态定义 动态定义
2.理解圆有关的概念:
同心圆(等圆)
弦:(直径)
弧:(半圆、优弧、劣弧)等弧
同课章节目录
