2022版高中数学第四章函数应用本章达标检测(word版含解析)北师大版必修1
文档属性
| 名称 | 2022版高中数学第四章函数应用本章达标检测(word版含解析)北师大版必修1 | 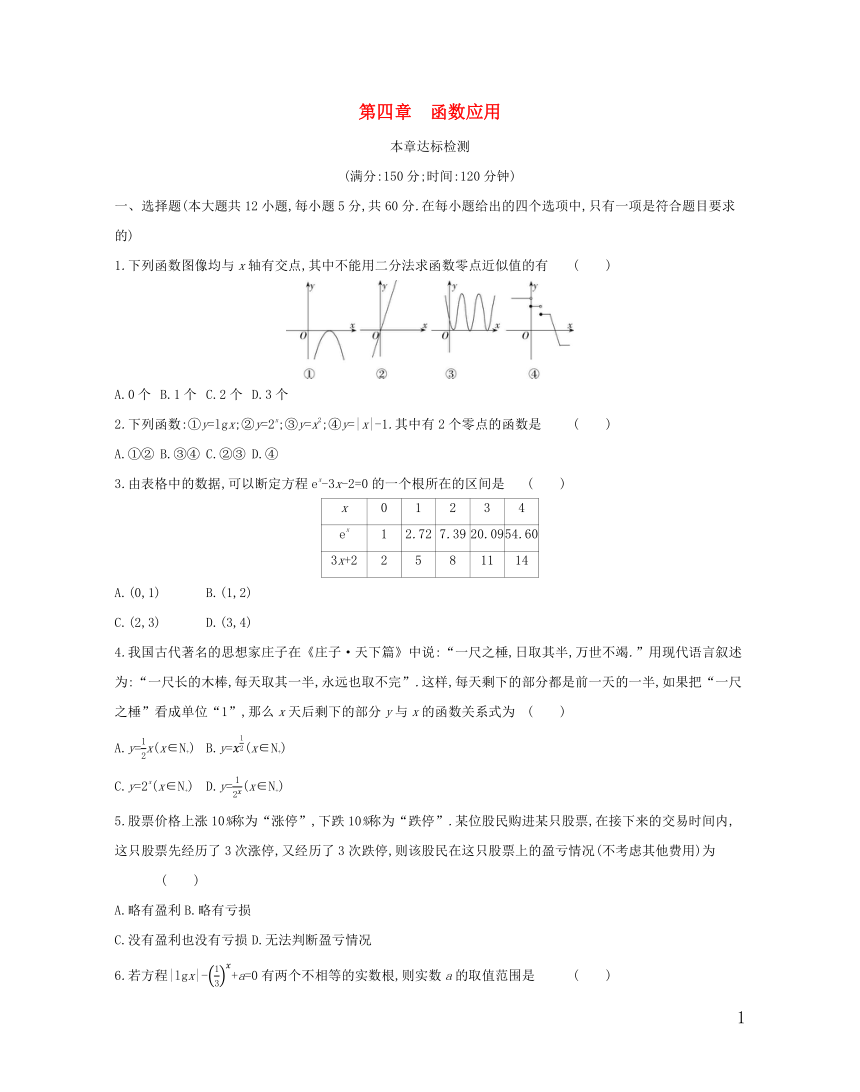 | |
| 格式 | zip | ||
| 文件大小 | 164.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 00:00:30 | ||
图片预览





文档简介
第四章 函数应用
本章达标检测
(满分:150分;时间:120分钟)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数图像均与x轴有交点,其中不能用二分法求函数零点近似值的有 ( )
A.0个 B.1个 C.2个 D.3个
2.下列函数:①y=lgx;②y=2x;③y=x2;④y=|x|-1.其中有2个零点的函数是 ( )
A.①② B.③④ C.②③ D.④
3.由表格中的数据,可以断定方程ex-3x-2=0的一个根所在的区间是 ( )
x 0 1 2 3 4
ex 1 2.72 7.39 20.09 54.60
3x+2 2 5 8 11 14
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
4.我国古代著名的思想家庄子在《庄子·天下篇》中说:“一尺之棰,日取其半,万世不竭.”用现代语言叙述为:“一尺长的木棒,每天取其一半,永远也取不完”.这样,每天剩下的部分都是前一天的一半,如果把“一尺之棰”看成单位“1”,那么x天后剩下的部分y与x的函数关系式为 ( )
A.y=x(x∈N+) B.y=(x∈N+)
C.y=2x(x∈N+) D.y=(x∈N+)
5.股票价格上涨10%称为“涨停”,下跌10%称为“跌停”.某位股民购进某只股票,在接下来的交易时间内,这只股票先经历了3次涨停,又经历了3次跌停,则该股民在这只股票上的盈亏情况(不考虑其他费用)为 ( )
A.略有盈利B.略有亏损
C.没有盈利也没有亏损 D.无法判断盈亏情况
6.若方程|lgx|-+a=0有两个不相等的实数根,则实数a的取值范围是 ( )
A. B.
C.(1,+∞) D.(-∞,1)
7.用二分法求函数f(x)=ln(x+1)+x-1在区间(0,1)上的零点的近似值,当精度为0.01时,所需二分区间的次数最少为 ( )
A.5 B.6 C.7 D.8
8.某种产品的有效期y(单位:天)与储藏的温度x(单位:℃)满足关系式y=ekx+b(e=2.71828…,k、b为常数),若该产品在0℃下的有效期为192天,在33℃下的有效期是24天,则该产品在22℃的有效期为 ( )
A.45天 B.46天 C.47天 D.48天
9.甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计).如果他在t4时刻卖出所有商品,那么他将获得的最大利润是( )
A.40万元 B.60万元 C.120万元 D.140万元
10.某桶装水运营部每天的固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表所示:
销售单价/元 6 7 8 9 10 11
日均销售量/桶 480 440 400 360 320 280
设销售单价在进价基础上增加x元后,日均销售利润为y元,则该运营部要想获得最大利润,每桶水的销售单价在进价的基础上应增加 ( )
A.3元 B.4元 C.5元 D.6.5元
11.已知定义在R上的函数f(x)满足条件f(x-2)=f(x),且函数y=f(x+1)为偶函数,当x∈[0,1]时,f(x)=2x-1,则方程f(x)-=0在[-1,3]上的实根之和为 ( )
A.4 B.3 C.2+log23 D.3-log23
12.定义在R上的函数f(x)=若关于x的方程[f(x)]2-mf(x)+m-1=0(其中m>2)有n个不同的实根x1,x2,…,xn,则f(x1+x2+…+xn)= ( )
A.5e B.4e C. D.
二、填空题(本大题共4小题,每小题5分,共20分.将答
案填在题中横线上)
13.方程-=0的实数根的个数为 .
14.用二分法求方程x3-2x-5=0在区间[2,4]上的实数根的近似值时,取中点x1=3,则下一个有根区间是 .
15.把物体放在冷空气中冷却,如果物体原来的温度是θ1℃,空气的温度是θ0℃,tmin后物体的温度θ(℃)可由公式θ=θ0+(θ1-θ0)e-0.24t求得.把温度是100℃的物体放在10℃的空气中冷却tmin后,物体的温度是40℃,那么t的值约等于 .(保留三位有效数字,参考数据:ln3取1.099)
16.已知f(x)=(x-2)·|x+1|,若关于x的方程f(x)=x+m有三个不同的实数解,则实数m的取值范围是 .
三、解答题(本大题共6小题,共70分.解答应写出文字
说明、证明过程或演算步骤)
17.(本小题满分10分)探究方程4x3+x-15=0在[1,2]内实数解的情况,并说明理由.
18.(本小题满分12分)已知函数f(x)=|x|+-1(x≠0).
(1)若对任意的x>0,不等式f(x)>0恒成立,求m的取值范围;
(2)试讨论函数f(x)零点的个数.
19.(本小题满分12分)某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如下表所示的关系(其中30≤x≤60,且x∈N*).
x 30 40 45 60
y 60 40 30 0
(1)在所给的平面直角坐标系中,根据表中提供的数据,描出实数对(x,y)的对应点,并确定y与x的一个函数关系式;
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价为多少元时,才能获得最大日销售利润.
20.(本小题满分12分)某城市上一年度电价为0.80元/千瓦时,年用电量为a千瓦时,本年度计划将电价降到0.55~0.7元/千瓦时之间,而居民用户期望电价为0.40元/千瓦时(该市电力成本价为0.30元/千瓦时).经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为0.2a,试问当地电价最低为多少元/千瓦时时,可保证电力部门的收益比上一年度至少增加20%
21.(本小题满分12分)食品安全问题越来越引起人们的重视,农药、化肥的滥用给人民群众的健康带来了一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入P(单位:万元)、种黄瓜的年收入Q(单位:万元)与投入a(单位:万元)分别满足关系式:P=80+4,Q=a+120,设甲大棚的投入为x(单位:万元),每年两个大棚的总收益为f(x)(单位:万元).
(1)求f(50)的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益f(x)最大
22.(本小题满分 12分)已知指数函数f(x)=ax(a>0且a≠1),函数g(x)与f(x)的图像关于y=x对称,h(x)=x2-2x+1.
(1)若a>1,F(x)=,证明F(x)为R上的增函数;
(2)若a=2,G(x)=h(x)-f(x),判断G(x)的零点个数(直接给出结论,不必说明理由或证明);
(3)若x∈(1,2)时,h(x)答案全解全析
函数应用
本章达标检测
1.C 2.D 3.C 4.D 5.B
6.B 7.C 8.D 9.C 10.D
11.A 12.C
一、选择题
1.C 由题意可知,若能利用二分法求函数零点的近似值,函数零点左右两侧的函数值符号相反,即该函数的图像穿过x轴,且该函数在零点附近的函数图像连续,因此,②④中能用二分法求函数零点近似值,①③中不能用二分法求函数零点近似值.故选C.
2.D 分别作出这四个函数的图像(图略),其中只有y=|x|-1的图像与x轴有2个交点,即函数有2个零点,故选D.
3.C 设f(x)=ex-3x-2,由题表知,f(0)、 f(1)、 f(2)均为负值,f(3)、 f(4)均为正值,又f(x)的图像是连续曲线,所以方程ex-3x-2=0的一个根所在的区间是(2,3),故选C.
4.D 由题意可得,剩下的部分依次为,,,…,因此x天后剩下的部分y与x的函数关系式为y=(x∈N+),故选D.
5.B ∵(1+10%)3(1-10%)3=0.993<1,∴该股民在这只股票上的盈亏情况是略有亏损.故选B.
6.B 方程|lgx|-+a=0可化为|lgx|=-a,设f(x)=|lgx|,g(x)=-a,在同一坐标系中作出两函数的图像,如图所示:
由图知,只需满足当x=1时,g(1)=-a>0,即a<.
7.C 开区间(0,1)的长度等于1,每经过一次操作,区间长度变为原来的一半,经过n次操作后,区间长度变为,n∈N+.
∵精度为0.01,
∴<0.01,
∴n≥7,n∈N+,
故所需二分区间的次数最少为7,故选C.
8.D y=ekx+b(e=2.718…,k,b为常数),当x=0时,eb=192,
当x=33时,e33k+b=24,∴e33k==,
e11k=,eb=192,∴当x=22时,e22k+b=·(eb)=×192=48,故选D.
9.C 要想获得最大利润,则甲的价格为6元/份时,全部买入,可以买120÷6=20(万份),价格为8元/份时,全部卖出,此过程获利20×2=40(万元);乙的价格为4元/份时,全部买入,可以买(120+40)÷4=40(万份),价格为6元/份时,全部卖出,此过程获利40×2=80(万元),∴共获利40+80=120(万元),故选C.
10.D 由题意可知每桶水的销售单价在进价的基础上增加x元时,
日均销售量为480-40(x+5-6)=(520-40x)桶,
故y=x(520-40x)-200=-40x2+520x-200=-40(x2-13x)-200=-40+1490,易知当x=时,ymax=1490,
故该运营部要想获得最大利润,每桶水的销售单价在进价的基础上应增加6.5元,故选D.
11.A 由f(x-2)=f(x),得f(x+2)=f(x),则f(x)是周期为2的周期函数.
又函数y=f(x+1)为偶函数,∴y=f(x+1)的图像关于y轴对称,则f(x)的图像关于直线x=1对称,又当x∈[0,1]时,f(x)=2x-1,
作出函数y=f(x)的图像如图:
由图可知,函数y=f(x)的图像与直线y=在[-1,3]上有4个交点,且两两关于直线x=1对称,
∴方程f(x)-=0在[-1,3]上的实根之和为4.故选A.
方法技巧
方程的根的问题,可以等价于函数的零点问题,函数零点的求法,首先看能否直接解方程得到解,若不容易解,则可转化成两个函数的交点问题,可以通过图像,直观简单地解决问题.
12.C 由[f(x)]2-mf(x)+m-1=0得[f(x)-1][f(x)-(m-1)]=0,
解得f(x)=1或f(x)=m-1>1.
作出函数y=f(x)的图像,如图所示:
由f(x)的图像知,f(x)=1有三个解,分别是e,x1,x2,且x1+x2=2e,f(x)=m-1有两个解,分别是x3,x4,且x3+x4=2e.
因此f(x1+x2+…+xn)=f(5e)=,故选C.
二、填空题
13.答案 1
解析 由-=0得=,
在同一坐标系中作出函数y=与y=的图像,如图所示:
由图像知,方程-=0有唯一实数根.
14.答案 (2,3)
解析 设f(x)=x3-2x-5,则f(2)<0,f(3)>0,f(4)>0,
故f(2)·f(3)<0,则下一个有根区间是(2,3).
15.答案 4.58
解析 由题意可得40=10+(100-10)·e-0.24t,化简,得e-0.24t=,
∴-0.24t=ln=-ln3,
∴0.24t=ln3=1.099,
∴t≈4.58.
16.答案 (-3,1)
解析 当x≥-1时,f(x)=(x-2)(x+1)=x2-x-2;当x<-1时,f(x)=-(x-2)(x+1)=-x2+x+2.
设y=x+m,
方程f(x)=x+m有三个不同的实数解,即函数y=f(x)和y=x+m的图像有三个不同的交点,
作出函数的图像,如图所示:
由图像可知,当y=x+m的图像经过点(-1,0)时,两个函数图像有两个交点,此时m=1.
若x>-1,则当y=x+m的图像与抛物线相切时,两个函数的图像有两个交点,
由f(x)=x2-x-2=x+m得,x2-2x-2-m=0,
对于方程x2-2x-2-m=0,Δ=4-4(-2-m)=0,即4+8+4m=0,∴m=-3,
此时y=x-3的图像与抛物线相切,
∴要使函数f(x)和y=x+m的图像有三个不同的交点,则-3三、解答题
17.解析 令f(x)=4x3+x-15,
∵f(1)=4+1-15=-10<0,f(2)=4×8+2-15=19>0,且f(x)的图像是连续曲线, (2分)
∴f(x)=4x3+x-15在[1,2]上存在零点.
∵y=4x3和y=x在[1,2]上都为增函数,
∴f(x)=4x3+x-15在[1,2]上为增函数,
∴方程4x3+x-15=0在[1,2]内的实数解是唯一的. (8分)
因此方程4x3+x-15=0在[1,2]内有唯一的实数解. (10分)
18.解析 (1)当x>0时,f(x)=x+-1,不等式f(x)>0恒成立等价于x+-1>0恒成立,则有m>x-x2对x>0恒成立,
而x-x2=-+≤(x>0),
故m>. (4分)
(2)令f(x)=|x|+-1=0,
得m= (5分)
令g(x)=
函数f(x)的零点个数,即y=m和y=g(x)=图像的交点个数.
在同一坐标系中作出函数y=m,y=g(x)的图像(如图).
(8分)
结合图像可知,
①当m>或m<-时,函数f(x)有一个零点;
②当m=±或m=0时,函数f(x)有两个零点;
③当-19.解析 (1)由题表中的数据,在平面直角坐标系中作出(30,60),(40,40),(45,30),(60,0)的对应点,
易知它们分布在一条直线上.
(3分)
设y=kx+b(k≠0)(30≤x≤60且x∈N*),
将点(45,30),(60,0)代入y=kx+b,得解得 (5分)
所以y=-2x+120(30≤x≤60且x∈N*), (6分)
经检验,(30,60),(40,40)也在此直线上,
所以所求函数解析式为y=-2x+120(30≤x≤60且x∈N*). (7分)
(2)依题意,得P=y(x-30)=(-2x+120)(x-30)=-2(x-60)(x-30)=-2x2+180x-3600=-2(x-45)2+450(30≤x≤60且x∈N*), (10分)
所以当x=45时,P有最大值,为450,
故销售单价为45元时,才能获得最大日销售利润. (12分)
20.解析 设新电价为x元/千瓦时(0.55≤x≤0.7),则新增用电量为千瓦时,依题意,有(x-0.3)≥a(0.8-0.3)×(1+20%), (4分)
即(x-0.2)(x-0.3)≥0.6(x-0.4),
整理,得x2-1.1x+0.3≥0, (5分)
解此不等式,得x≥0.6或x≤0.5,
又0.55≤x≤0.7,
所以0.6≤x≤0.7, (9分)
因此,xmin=0.6,即电价最低为0.6元/千瓦时时,可保证电力部门的收益比上一年度至少增加20%. (12分)
21.解析 (1)∵甲大棚投入了50万元,则乙大棚投入了150万元,∴f(50)=80+4+×150+120=277.5. (4分)
(2)f(x)=80+4+(200-x)+120=-x+4+250,
依题意得 20≤x≤180, (7分)
故f(x)=-x+4+250(20≤x≤180).
令t=,则t∈[2,6],∴g(t)=-t2+4t+250=-(t-8)2+282, (9分)
当t=8,即x=128时,f(x)max=282,
此时乙大棚的投入为200-128=72(万元),
所以甲大棚投入128万元,乙大棚投入72万元时,总收益最大,且最大总收益为282万元. (12分)
22.解析 (1)证明:由题知F(x)===1-. (2分)
任取x1,x2∈R,且x1F(x1)-F(x2)=1--=. (4分)
∵a>1,∴>,(+1)(+1)>0,
∴F(x1)∴F(x)为R上的增函数. (6分)
(2)G(x)有3个零点. (8分)
(3)∵函数g(x)与f(x)的图像关于y=x对称,∴g(x)与f(x)互为反函数,
∴g(x)=logax(a>0,且a≠1), (9分)
易知h(x)=x2-2x+1=(x-1)2.
当0当a>1,x∈(1,2)时,要使h(x)综上所述,a的取值范围是(1,2]. (12分)
12
本章达标检测
(满分:150分;时间:120分钟)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数图像均与x轴有交点,其中不能用二分法求函数零点近似值的有 ( )
A.0个 B.1个 C.2个 D.3个
2.下列函数:①y=lgx;②y=2x;③y=x2;④y=|x|-1.其中有2个零点的函数是 ( )
A.①② B.③④ C.②③ D.④
3.由表格中的数据,可以断定方程ex-3x-2=0的一个根所在的区间是 ( )
x 0 1 2 3 4
ex 1 2.72 7.39 20.09 54.60
3x+2 2 5 8 11 14
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
4.我国古代著名的思想家庄子在《庄子·天下篇》中说:“一尺之棰,日取其半,万世不竭.”用现代语言叙述为:“一尺长的木棒,每天取其一半,永远也取不完”.这样,每天剩下的部分都是前一天的一半,如果把“一尺之棰”看成单位“1”,那么x天后剩下的部分y与x的函数关系式为 ( )
A.y=x(x∈N+) B.y=(x∈N+)
C.y=2x(x∈N+) D.y=(x∈N+)
5.股票价格上涨10%称为“涨停”,下跌10%称为“跌停”.某位股民购进某只股票,在接下来的交易时间内,这只股票先经历了3次涨停,又经历了3次跌停,则该股民在这只股票上的盈亏情况(不考虑其他费用)为 ( )
A.略有盈利B.略有亏损
C.没有盈利也没有亏损 D.无法判断盈亏情况
6.若方程|lgx|-+a=0有两个不相等的实数根,则实数a的取值范围是 ( )
A. B.
C.(1,+∞) D.(-∞,1)
7.用二分法求函数f(x)=ln(x+1)+x-1在区间(0,1)上的零点的近似值,当精度为0.01时,所需二分区间的次数最少为 ( )
A.5 B.6 C.7 D.8
8.某种产品的有效期y(单位:天)与储藏的温度x(单位:℃)满足关系式y=ekx+b(e=2.71828…,k、b为常数),若该产品在0℃下的有效期为192天,在33℃下的有效期是24天,则该产品在22℃的有效期为 ( )
A.45天 B.46天 C.47天 D.48天
9.甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计).如果他在t4时刻卖出所有商品,那么他将获得的最大利润是( )
A.40万元 B.60万元 C.120万元 D.140万元
10.某桶装水运营部每天的固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表所示:
销售单价/元 6 7 8 9 10 11
日均销售量/桶 480 440 400 360 320 280
设销售单价在进价基础上增加x元后,日均销售利润为y元,则该运营部要想获得最大利润,每桶水的销售单价在进价的基础上应增加 ( )
A.3元 B.4元 C.5元 D.6.5元
11.已知定义在R上的函数f(x)满足条件f(x-2)=f(x),且函数y=f(x+1)为偶函数,当x∈[0,1]时,f(x)=2x-1,则方程f(x)-=0在[-1,3]上的实根之和为 ( )
A.4 B.3 C.2+log23 D.3-log23
12.定义在R上的函数f(x)=若关于x的方程[f(x)]2-mf(x)+m-1=0(其中m>2)有n个不同的实根x1,x2,…,xn,则f(x1+x2+…+xn)= ( )
A.5e B.4e C. D.
二、填空题(本大题共4小题,每小题5分,共20分.将答
案填在题中横线上)
13.方程-=0的实数根的个数为 .
14.用二分法求方程x3-2x-5=0在区间[2,4]上的实数根的近似值时,取中点x1=3,则下一个有根区间是 .
15.把物体放在冷空气中冷却,如果物体原来的温度是θ1℃,空气的温度是θ0℃,tmin后物体的温度θ(℃)可由公式θ=θ0+(θ1-θ0)e-0.24t求得.把温度是100℃的物体放在10℃的空气中冷却tmin后,物体的温度是40℃,那么t的值约等于 .(保留三位有效数字,参考数据:ln3取1.099)
16.已知f(x)=(x-2)·|x+1|,若关于x的方程f(x)=x+m有三个不同的实数解,则实数m的取值范围是 .
三、解答题(本大题共6小题,共70分.解答应写出文字
说明、证明过程或演算步骤)
17.(本小题满分10分)探究方程4x3+x-15=0在[1,2]内实数解的情况,并说明理由.
18.(本小题满分12分)已知函数f(x)=|x|+-1(x≠0).
(1)若对任意的x>0,不等式f(x)>0恒成立,求m的取值范围;
(2)试讨论函数f(x)零点的个数.
19.(本小题满分12分)某商场经销一批进价为每件30元的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如下表所示的关系(其中30≤x≤60,且x∈N*).
x 30 40 45 60
y 60 40 30 0
(1)在所给的平面直角坐标系中,根据表中提供的数据,描出实数对(x,y)的对应点,并确定y与x的一个函数关系式;
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价为多少元时,才能获得最大日销售利润.
20.(本小题满分12分)某城市上一年度电价为0.80元/千瓦时,年用电量为a千瓦时,本年度计划将电价降到0.55~0.7元/千瓦时之间,而居民用户期望电价为0.40元/千瓦时(该市电力成本价为0.30元/千瓦时).经测算,下调电价后,该城市新增用电量与实际电价和用户期望电价之差成反比,比例系数为0.2a,试问当地电价最低为多少元/千瓦时时,可保证电力部门的收益比上一年度至少增加20%
21.(本小题满分12分)食品安全问题越来越引起人们的重视,农药、化肥的滥用给人民群众的健康带来了一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入P(单位:万元)、种黄瓜的年收入Q(单位:万元)与投入a(单位:万元)分别满足关系式:P=80+4,Q=a+120,设甲大棚的投入为x(单位:万元),每年两个大棚的总收益为f(x)(单位:万元).
(1)求f(50)的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益f(x)最大
22.(本小题满分 12分)已知指数函数f(x)=ax(a>0且a≠1),函数g(x)与f(x)的图像关于y=x对称,h(x)=x2-2x+1.
(1)若a>1,F(x)=,证明F(x)为R上的增函数;
(2)若a=2,G(x)=h(x)-f(x),判断G(x)的零点个数(直接给出结论,不必说明理由或证明);
(3)若x∈(1,2)时,h(x)
函数应用
本章达标检测
1.C 2.D 3.C 4.D 5.B
6.B 7.C 8.D 9.C 10.D
11.A 12.C
一、选择题
1.C 由题意可知,若能利用二分法求函数零点的近似值,函数零点左右两侧的函数值符号相反,即该函数的图像穿过x轴,且该函数在零点附近的函数图像连续,因此,②④中能用二分法求函数零点近似值,①③中不能用二分法求函数零点近似值.故选C.
2.D 分别作出这四个函数的图像(图略),其中只有y=|x|-1的图像与x轴有2个交点,即函数有2个零点,故选D.
3.C 设f(x)=ex-3x-2,由题表知,f(0)、 f(1)、 f(2)均为负值,f(3)、 f(4)均为正值,又f(x)的图像是连续曲线,所以方程ex-3x-2=0的一个根所在的区间是(2,3),故选C.
4.D 由题意可得,剩下的部分依次为,,,…,因此x天后剩下的部分y与x的函数关系式为y=(x∈N+),故选D.
5.B ∵(1+10%)3(1-10%)3=0.993<1,∴该股民在这只股票上的盈亏情况是略有亏损.故选B.
6.B 方程|lgx|-+a=0可化为|lgx|=-a,设f(x)=|lgx|,g(x)=-a,在同一坐标系中作出两函数的图像,如图所示:
由图知,只需满足当x=1时,g(1)=-a>0,即a<.
7.C 开区间(0,1)的长度等于1,每经过一次操作,区间长度变为原来的一半,经过n次操作后,区间长度变为,n∈N+.
∵精度为0.01,
∴<0.01,
∴n≥7,n∈N+,
故所需二分区间的次数最少为7,故选C.
8.D y=ekx+b(e=2.718…,k,b为常数),当x=0时,eb=192,
当x=33时,e33k+b=24,∴e33k==,
e11k=,eb=192,∴当x=22时,e22k+b=·(eb)=×192=48,故选D.
9.C 要想获得最大利润,则甲的价格为6元/份时,全部买入,可以买120÷6=20(万份),价格为8元/份时,全部卖出,此过程获利20×2=40(万元);乙的价格为4元/份时,全部买入,可以买(120+40)÷4=40(万份),价格为6元/份时,全部卖出,此过程获利40×2=80(万元),∴共获利40+80=120(万元),故选C.
10.D 由题意可知每桶水的销售单价在进价的基础上增加x元时,
日均销售量为480-40(x+5-6)=(520-40x)桶,
故y=x(520-40x)-200=-40x2+520x-200=-40(x2-13x)-200=-40+1490,易知当x=时,ymax=1490,
故该运营部要想获得最大利润,每桶水的销售单价在进价的基础上应增加6.5元,故选D.
11.A 由f(x-2)=f(x),得f(x+2)=f(x),则f(x)是周期为2的周期函数.
又函数y=f(x+1)为偶函数,∴y=f(x+1)的图像关于y轴对称,则f(x)的图像关于直线x=1对称,又当x∈[0,1]时,f(x)=2x-1,
作出函数y=f(x)的图像如图:
由图可知,函数y=f(x)的图像与直线y=在[-1,3]上有4个交点,且两两关于直线x=1对称,
∴方程f(x)-=0在[-1,3]上的实根之和为4.故选A.
方法技巧
方程的根的问题,可以等价于函数的零点问题,函数零点的求法,首先看能否直接解方程得到解,若不容易解,则可转化成两个函数的交点问题,可以通过图像,直观简单地解决问题.
12.C 由[f(x)]2-mf(x)+m-1=0得[f(x)-1][f(x)-(m-1)]=0,
解得f(x)=1或f(x)=m-1>1.
作出函数y=f(x)的图像,如图所示:
由f(x)的图像知,f(x)=1有三个解,分别是e,x1,x2,且x1+x2=2e,f(x)=m-1有两个解,分别是x3,x4,且x3+x4=2e.
因此f(x1+x2+…+xn)=f(5e)=,故选C.
二、填空题
13.答案 1
解析 由-=0得=,
在同一坐标系中作出函数y=与y=的图像,如图所示:
由图像知,方程-=0有唯一实数根.
14.答案 (2,3)
解析 设f(x)=x3-2x-5,则f(2)<0,f(3)>0,f(4)>0,
故f(2)·f(3)<0,则下一个有根区间是(2,3).
15.答案 4.58
解析 由题意可得40=10+(100-10)·e-0.24t,化简,得e-0.24t=,
∴-0.24t=ln=-ln3,
∴0.24t=ln3=1.099,
∴t≈4.58.
16.答案 (-3,1)
解析 当x≥-1时,f(x)=(x-2)(x+1)=x2-x-2;当x<-1时,f(x)=-(x-2)(x+1)=-x2+x+2.
设y=x+m,
方程f(x)=x+m有三个不同的实数解,即函数y=f(x)和y=x+m的图像有三个不同的交点,
作出函数的图像,如图所示:
由图像可知,当y=x+m的图像经过点(-1,0)时,两个函数图像有两个交点,此时m=1.
若x>-1,则当y=x+m的图像与抛物线相切时,两个函数的图像有两个交点,
由f(x)=x2-x-2=x+m得,x2-2x-2-m=0,
对于方程x2-2x-2-m=0,Δ=4-4(-2-m)=0,即4+8+4m=0,∴m=-3,
此时y=x-3的图像与抛物线相切,
∴要使函数f(x)和y=x+m的图像有三个不同的交点,则-3
17.解析 令f(x)=4x3+x-15,
∵f(1)=4+1-15=-10<0,f(2)=4×8+2-15=19>0,且f(x)的图像是连续曲线, (2分)
∴f(x)=4x3+x-15在[1,2]上存在零点.
∵y=4x3和y=x在[1,2]上都为增函数,
∴f(x)=4x3+x-15在[1,2]上为增函数,
∴方程4x3+x-15=0在[1,2]内的实数解是唯一的. (8分)
因此方程4x3+x-15=0在[1,2]内有唯一的实数解. (10分)
18.解析 (1)当x>0时,f(x)=x+-1,不等式f(x)>0恒成立等价于x+-1>0恒成立,则有m>x-x2对x>0恒成立,
而x-x2=-+≤(x>0),
故m>. (4分)
(2)令f(x)=|x|+-1=0,
得m= (5分)
令g(x)=
函数f(x)的零点个数,即y=m和y=g(x)=图像的交点个数.
在同一坐标系中作出函数y=m,y=g(x)的图像(如图).
(8分)
结合图像可知,
①当m>或m<-时,函数f(x)有一个零点;
②当m=±或m=0时,函数f(x)有两个零点;
③当-
易知它们分布在一条直线上.
(3分)
设y=kx+b(k≠0)(30≤x≤60且x∈N*),
将点(45,30),(60,0)代入y=kx+b,得解得 (5分)
所以y=-2x+120(30≤x≤60且x∈N*), (6分)
经检验,(30,60),(40,40)也在此直线上,
所以所求函数解析式为y=-2x+120(30≤x≤60且x∈N*). (7分)
(2)依题意,得P=y(x-30)=(-2x+120)(x-30)=-2(x-60)(x-30)=-2x2+180x-3600=-2(x-45)2+450(30≤x≤60且x∈N*), (10分)
所以当x=45时,P有最大值,为450,
故销售单价为45元时,才能获得最大日销售利润. (12分)
20.解析 设新电价为x元/千瓦时(0.55≤x≤0.7),则新增用电量为千瓦时,依题意,有(x-0.3)≥a(0.8-0.3)×(1+20%), (4分)
即(x-0.2)(x-0.3)≥0.6(x-0.4),
整理,得x2-1.1x+0.3≥0, (5分)
解此不等式,得x≥0.6或x≤0.5,
又0.55≤x≤0.7,
所以0.6≤x≤0.7, (9分)
因此,xmin=0.6,即电价最低为0.6元/千瓦时时,可保证电力部门的收益比上一年度至少增加20%. (12分)
21.解析 (1)∵甲大棚投入了50万元,则乙大棚投入了150万元,∴f(50)=80+4+×150+120=277.5. (4分)
(2)f(x)=80+4+(200-x)+120=-x+4+250,
依题意得 20≤x≤180, (7分)
故f(x)=-x+4+250(20≤x≤180).
令t=,则t∈[2,6],∴g(t)=-t2+4t+250=-(t-8)2+282, (9分)
当t=8,即x=128时,f(x)max=282,
此时乙大棚的投入为200-128=72(万元),
所以甲大棚投入128万元,乙大棚投入72万元时,总收益最大,且最大总收益为282万元. (12分)
22.解析 (1)证明:由题知F(x)===1-. (2分)
任取x1,x2∈R,且x1
∵a>1,∴>,(+1)(+1)>0,
∴F(x1)
(2)G(x)有3个零点. (8分)
(3)∵函数g(x)与f(x)的图像关于y=x对称,∴g(x)与f(x)互为反函数,
∴g(x)=logax(a>0,且a≠1), (9分)
易知h(x)=x2-2x+1=(x-1)2.
当0
12
