不等式复习课
图片预览








文档简介
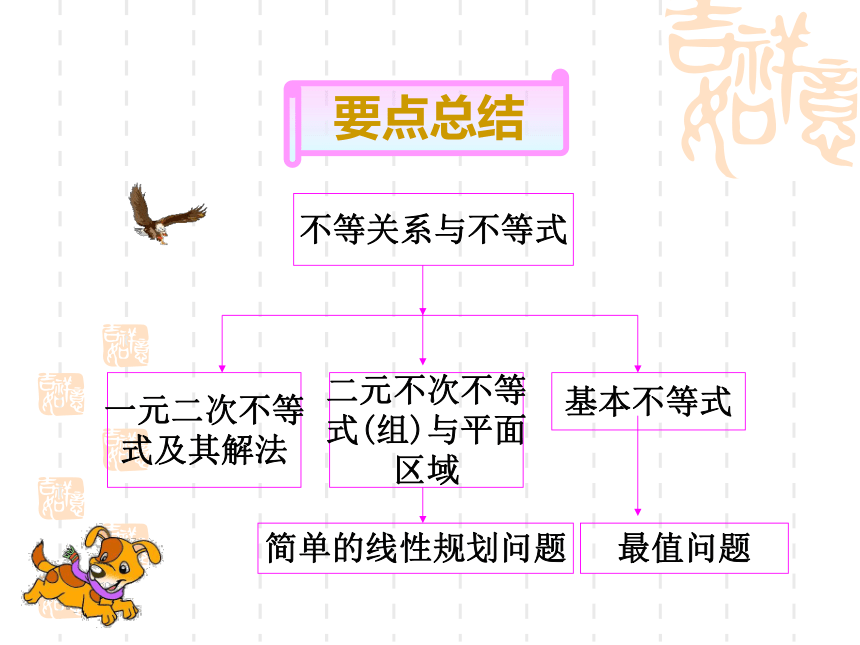
课件20张PPT。第三章 不等式要点总结不等关系与不等式一元二次不等
式及其解法二元不次不等
式(组)与平面
区域简单的线性规划问题基本不等式最值问题1、代数式的大小比较或证明通常用
作差比较法;2、比较大小或证明的一般过程为:作差,化积,判断,结论;3.1 不等关系与不等式3、不等式的性质:1、一元二次不等式的定义 我们把只含有一个未知数,并且未知数的最高次数为2次的不等式称为一元二次不等式.3.2 一元二次不等式及其解法2、一元二次方程的一般形式3、解一元二次不等式的基本步骤:“三步曲”(1)转化为不等式的“标准”形式;(2)算△,解相应一元二次方程的根;(3)根据二次函数的图象以及不等号的方向,写出不等式的解集.
(a>0)的图像有两相异实根有两相等实根的解集的解集无实根R例1:如果关于 的不等式
的解集是
,求关于 的不等式
的解集。
例2:学案89页20解:例2:已知
(1)解关于 的不等式
(2)若不等式 的解集为
求实数 的值。3.4基本不等式(当且仅当a=b时,等号成立) (1)(3)1.2、两个正数的和为定值时,它们的积有最大值,即若
a,b∈R+,且a+b=M,M为定值,则ab等号当且仅当a=b时成立. 3、两个正数的积为定值时,它们的和有最小值,即若
a,b∈R+,且ab=P,P为定值,则a+b 等号当且仅当a=b时成立 .4、应用基本不等式时,主要用到的方法和技巧是:凑、拆,使之出现和为定值或积为定值特征.例:学案90页21,22谢谢!
式及其解法二元不次不等
式(组)与平面
区域简单的线性规划问题基本不等式最值问题1、代数式的大小比较或证明通常用
作差比较法;2、比较大小或证明的一般过程为:作差,化积,判断,结论;3.1 不等关系与不等式3、不等式的性质:1、一元二次不等式的定义 我们把只含有一个未知数,并且未知数的最高次数为2次的不等式称为一元二次不等式.3.2 一元二次不等式及其解法2、一元二次方程的一般形式3、解一元二次不等式的基本步骤:“三步曲”(1)转化为不等式的“标准”形式;(2)算△,解相应一元二次方程的根;(3)根据二次函数的图象以及不等号的方向,写出不等式的解集.
(a>0)的图像有两相异实根有两相等实根的解集的解集无实根R例1:如果关于 的不等式
的解集是
,求关于 的不等式
的解集。
例2:学案89页20解:例2:已知
(1)解关于 的不等式
(2)若不等式 的解集为
求实数 的值。3.4基本不等式(当且仅当a=b时,等号成立) (1)(3)1.2、两个正数的和为定值时,它们的积有最大值,即若
a,b∈R+,且a+b=M,M为定值,则ab等号当且仅当a=b时成立. 3、两个正数的积为定值时,它们的和有最小值,即若
a,b∈R+,且ab=P,P为定值,则a+b 等号当且仅当a=b时成立 .4、应用基本不等式时,主要用到的方法和技巧是:凑、拆,使之出现和为定值或积为定值特征.例:学案90页21,22谢谢!
