人教版数学八年级下册 16.3.2 二次根式的混合运算1 (共26张ppt)
文档属性
| 名称 | 人教版数学八年级下册 16.3.2 二次根式的混合运算1 (共26张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-15 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
16.3.2二次根式的混合运算
二个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个含有二次根式的代数式互为有理化因式.
例如:
的有理化因式是
的有理化因式是
的有理化因式是
指出下列各式的有理化因式
一. 分母有理化常规基本法
练习
二.分解约简法
化简
练习
解
例题3 如图,在面积为 的正方形 中,截得直角三角形 的面积为 ,求 的长.
因为正方形
面积为
所以
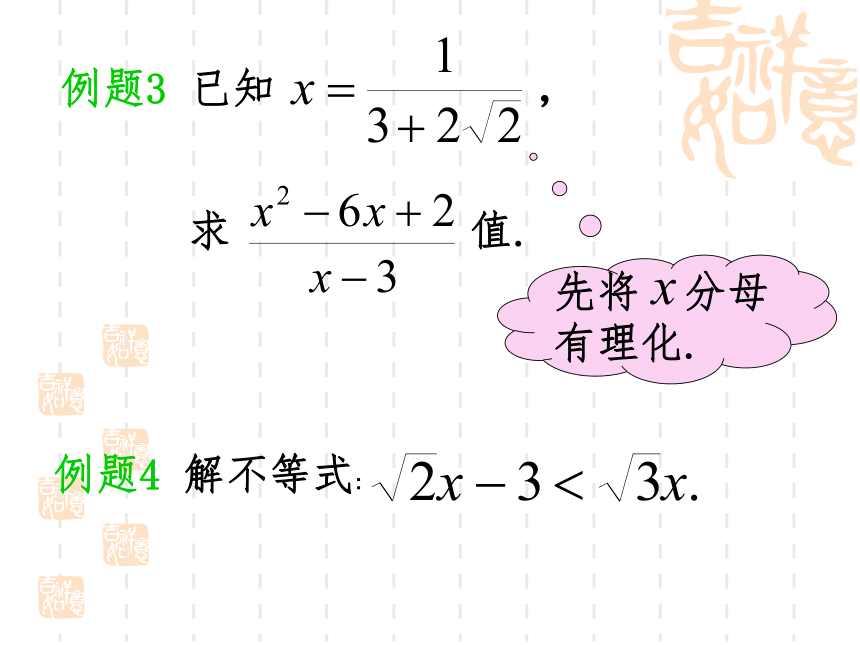
例题3 已知 ,
求 值.
例题4 解不等式:
先将 分母有理化.
复习
问题
怎样计算下式?观察所得的积是否含有二次根式?
含有二次根式
不含二次根式
两个含有二次根式的非零代数式相乘,如果它们的积不含有二次根式,就说这两个含有二次根式的非零代数式互为有理化因式.
与 互为有理化因式.
再见
复习
计算
问题
怎样计算下式?观察所得的积是否含有二次根式?
含有二次根式
不含二次根式
两个含有二次根式的非零代数式相乘,如果它们的积不含有二次根式,就说这两个含有二次根式的非零代数式互为有理化因式.
与 互为有理化因式.
的有理化因式为 ;
的有理化因式为 ;
的有理化因式为 ;
的有理化因式为 .
想一想
例题1 把下列各式分母有理化:
分子和分母都乘以分母的有理化因式.
例题2 计算:
先将每一项分母有理化.
例:计算(1)
计算
(3)
(2)
(1)
比较根式的大小.
提高题
解:
13
7
14
6
+
+
14
6
+
=
( )
2
6+2 +14=20+2
√
84
√
84
∵
( )
13
7
+
2
=
20+2
91
0
14
6
+
0
13
7
+
又
∵
复习
计算
例题4 解下列方程和不等式:
复习
计算
五、二次根式的混合运算
例1、计算
例2、计算
例题4 解下列方程和不等式:
16.3.2二次根式的混合运算
二个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个含有二次根式的代数式互为有理化因式.
例如:
的有理化因式是
的有理化因式是
的有理化因式是
指出下列各式的有理化因式
一. 分母有理化常规基本法
练习
二.分解约简法
化简
练习
解
例题3 如图,在面积为 的正方形 中,截得直角三角形 的面积为 ,求 的长.
因为正方形
面积为
所以
例题3 已知 ,
求 值.
例题4 解不等式:
先将 分母有理化.
复习
问题
怎样计算下式?观察所得的积是否含有二次根式?
含有二次根式
不含二次根式
两个含有二次根式的非零代数式相乘,如果它们的积不含有二次根式,就说这两个含有二次根式的非零代数式互为有理化因式.
与 互为有理化因式.
再见
复习
计算
问题
怎样计算下式?观察所得的积是否含有二次根式?
含有二次根式
不含二次根式
两个含有二次根式的非零代数式相乘,如果它们的积不含有二次根式,就说这两个含有二次根式的非零代数式互为有理化因式.
与 互为有理化因式.
的有理化因式为 ;
的有理化因式为 ;
的有理化因式为 ;
的有理化因式为 .
想一想
例题1 把下列各式分母有理化:
分子和分母都乘以分母的有理化因式.
例题2 计算:
先将每一项分母有理化.
例:计算(1)
计算
(3)
(2)
(1)
比较根式的大小.
提高题
解:
13
7
14
6
+
+
14
6
+
=
( )
2
6+2 +14=20+2
√
84
√
84
∵
( )
13
7
+
2
=
20+2
91
0
14
6
+
0
13
7
+
又
∵
复习
计算
例题4 解下列方程和不等式:
复习
计算
五、二次根式的混合运算
例1、计算
例2、计算
例题4 解下列方程和不等式:
