人教版数学八年级下册 19.3 一次函数-待定系数法 课件(共15张PPT)
文档属性
| 名称 | 人教版数学八年级下册 19.3 一次函数-待定系数法 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-16 13:49:25 | ||
图片预览






文档简介
(共15张PPT)
学习目标:
了解待定系数法的思维方式与特点;
会根据所给信息用待定系数法求一次函数解析式,发展解决问题的能力;
进一步体验并初步形成“数形结合”的思想方法
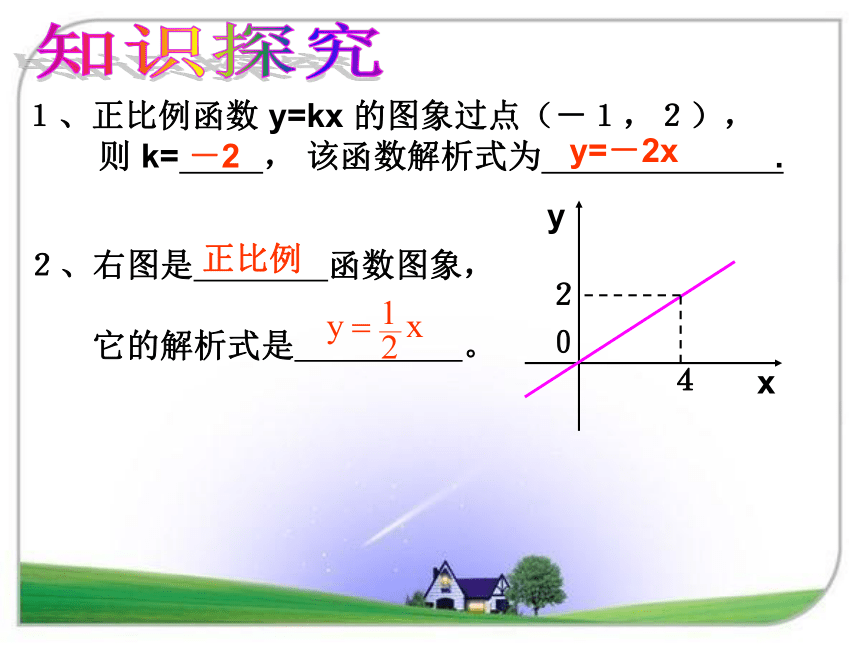
1、正比例函数 y=kx 的图象过点(-1,2),
则 k= , 该函数解析式为 .
2、右图是 函数图象,
它的解析式是 。
-2
y=-2x
0
2
4
y
x
正比例
3已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式。
解:设这个一次函数的解析式为y = kx+b
∵图象过点(3,5)和(-4,-9), ∴
由①-②得
∴这个函数的解析式为y = 2x-1
①
②
y
x
5
3
-4
-9
0
A
B
先设出函数解析式,再根据条件确定解析式中未知的_____,从而具体写出这个式子的方法,叫做____________.
概念:待定系数法
系数
待定系数法
归纳:用待定系数法求一次函数解析式的步骤
①设出一次函数解析式________;
②根据条件确定解析式中未知的系数__________;
③将 k、b 代入 y=kx+b,得到所求函数解析式.
y=kx+b
k、b
0
6
4
y
x
-3
y = kx+b
1、根据图象求出函数解析式
解方程组得
k=
b=6
这个一次函数的解析式为:
2、已知一次函数y=kx+b(k≠0)平行于直线y=3x,且过点(1,4),求函数解析式
∴一次函数解析式为:y=3x+1
解: ∵一次函数y=kx+b(k≠0 )与直线y=3x平行
∴k=3
又∵一次函数y=3x+b过点(1,4)
∴3+b=4
b=1
3、已知一次函数y=kx-2(k≠0) ,且过点(1,3),求函数解析式
解: ∵一次函数y=kx-2( k≠0 )过点(1,3),
∴k-2=3
∴这个函数的解析式为y=5x-2
解得,k=5
4、在直角坐标系中,一次函数y=kx+b的图象经过三
点A(2,0)、B(0,2)、C(m,3),求这个函数
的关系式,并求m的值。
解: ∵一次函数y=kx+b过点A(2,0)、B(0,2),
∴
∴
∴一次函数的解析式为y=-x+2
又∵一次函数y=-x+2过点C(m,3)
∴-m+2=3 解得,m=-1 。
已知一次函数的图象经过点A(2,-1)和点B,其中点B是另一条直线 与y轴的交点,求这个一次函数的表达式。
解:设这个一次函数的解析式为y = kx+b,由已知可知
点B是直线 与y轴交点, ∴点B(0,3)
∴一次函数y=kx+b过点A(2,-1)、B(0,3),
∴
∴
∴这个函数的解析式为y=-2x+3
2、某车油箱现有汽油50升,行驶时,油箱中的余油量y(升)
是行驶路程x(km)的一次函数,其图象如图所示
求y与x的函数关系式,并写出自变量x的取值范围。
60
50
30
0
x/km
y/升
解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以
①
②
解得
1、已知一次函数解析式如何画它的函数图象?
函数解析式
y = kx+b
选取
满足条件的两定点
(x1,y1)与(x2,y2)
画出
一次函数的
图象:直线
选取
解出
2、已知一次函数的图象怎样求它的函数解析式?
x
y
2
-3
-4
-1
y = kx+b
学习目标:
了解待定系数法的思维方式与特点;
会根据所给信息用待定系数法求一次函数解析式,发展解决问题的能力;
进一步体验并初步形成“数形结合”的思想方法
1、正比例函数 y=kx 的图象过点(-1,2),
则 k= , 该函数解析式为 .
2、右图是 函数图象,
它的解析式是 。
-2
y=-2x
0
2
4
y
x
正比例
3已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式。
解:设这个一次函数的解析式为y = kx+b
∵图象过点(3,5)和(-4,-9), ∴
由①-②得
∴这个函数的解析式为y = 2x-1
①
②
y
x
5
3
-4
-9
0
A
B
先设出函数解析式,再根据条件确定解析式中未知的_____,从而具体写出这个式子的方法,叫做____________.
概念:待定系数法
系数
待定系数法
归纳:用待定系数法求一次函数解析式的步骤
①设出一次函数解析式________;
②根据条件确定解析式中未知的系数__________;
③将 k、b 代入 y=kx+b,得到所求函数解析式.
y=kx+b
k、b
0
6
4
y
x
-3
y = kx+b
1、根据图象求出函数解析式
解方程组得
k=
b=6
这个一次函数的解析式为:
2、已知一次函数y=kx+b(k≠0)平行于直线y=3x,且过点(1,4),求函数解析式
∴一次函数解析式为:y=3x+1
解: ∵一次函数y=kx+b(k≠0 )与直线y=3x平行
∴k=3
又∵一次函数y=3x+b过点(1,4)
∴3+b=4
b=1
3、已知一次函数y=kx-2(k≠0) ,且过点(1,3),求函数解析式
解: ∵一次函数y=kx-2( k≠0 )过点(1,3),
∴k-2=3
∴这个函数的解析式为y=5x-2
解得,k=5
4、在直角坐标系中,一次函数y=kx+b的图象经过三
点A(2,0)、B(0,2)、C(m,3),求这个函数
的关系式,并求m的值。
解: ∵一次函数y=kx+b过点A(2,0)、B(0,2),
∴
∴
∴一次函数的解析式为y=-x+2
又∵一次函数y=-x+2过点C(m,3)
∴-m+2=3 解得,m=-1 。
已知一次函数的图象经过点A(2,-1)和点B,其中点B是另一条直线 与y轴的交点,求这个一次函数的表达式。
解:设这个一次函数的解析式为y = kx+b,由已知可知
点B是直线 与y轴交点, ∴点B(0,3)
∴一次函数y=kx+b过点A(2,-1)、B(0,3),
∴
∴
∴这个函数的解析式为y=-2x+3
2、某车油箱现有汽油50升,行驶时,油箱中的余油量y(升)
是行驶路程x(km)的一次函数,其图象如图所示
求y与x的函数关系式,并写出自变量x的取值范围。
60
50
30
0
x/km
y/升
解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以
①
②
解得
1、已知一次函数解析式如何画它的函数图象?
函数解析式
y = kx+b
选取
满足条件的两定点
(x1,y1)与(x2,y2)
画出
一次函数的
图象:直线
选取
解出
2、已知一次函数的图象怎样求它的函数解析式?
x
y
2
-3
-4
-1
y = kx+b
